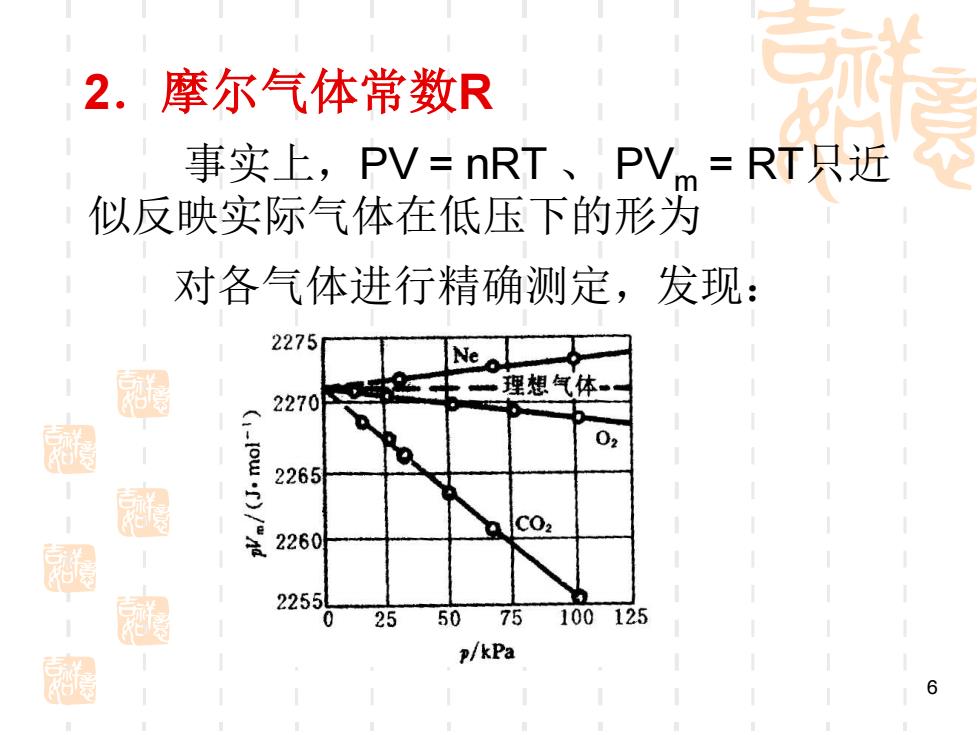
2.摩尔气体常数R 事实上,PV=nRT、PVm=RT只近 似反映实际气体在低压下的形为 对各气体进行精确测定,发现: 2275 Ne 士一理想气体 2270 -)/nd 2265 C02 2260 2255 0 25 50 75 100125 p/kPa 6
6 2.摩尔气体常数R 事实上,PV = nRT 、 PVm = RT只近 似反映实际气体在低压下的形为 对各气体进行精确测定,发现:

可知同一气体在不同的条件下偏离 PVm=RT程度也不同。从图中可看出:压 力越低,气体的PVT行为越接近于PVm= RT。 将不同气体的PVT对P作图,并外推 至P=0,得R=8.3145Jmo1K-1.这就是R的 来源,也说明在压力趋于0时,各种气体均 思 符合理想气体状态方程。 超
7 可知同一气体在不同的条件下偏离 PVm = RT程度也不同。从图中可看出:压 力越低,气体的PVT行为越接近于PVm = RT。 将不同气体的PVm /T对P作图,并外推 至P=0,得R=8.3145Jmol-1 K-1。这就是R的 来源,也说明在压力趋于0时,各种气体均 符合理想气体状态方程

3.理想气体的定义及微观模型 (1)PV=nRT所反映的气体PVT行为称 理想气体行为。 (2)凡在任何条件下均服从PV=nRT的气体 称理想气体,或PV=nRT是理想气体的数 学模型。 (3)在P→0的极限条件下,实际各气体均 圈 均服从PV=nRT。压力越低,方程越准确。 超 8
8 3.理想气体的定义及微观模型 (1) PV = nRT所反映的气体PVT行为称 理想气体行为。 (2) 凡在任何条件下均服从PV = nRT的气体 称理想气体,或PV = nRT是理想气体的数 学模型。 (3) 在P→0的极限条件下,实际各气体均 均服从PV = nRT。压力越低,方程越准确

根据理想气体定义,理想气体必须具 有以下两个特征(从气体分子运动论的发展 也得到证明): 1)气体分子是无体积的质点 黑 2)分子间无作用力 超 这也是理想气体的微观模型。 理想气体是一种分子本身没有体积、分 子之间无相互作用力的气体。 形调 9
9 根据理想气体定义,理想气体必须具 有以下两个特征 (从气体分子运动论的发展 也得到证明) : 1) 气体分子是无体积的质点 2) 分子间无作用力 这也是理想气体的微观模型。 理想气体是一种分子本身没有体积、分 子之间无相互作用力的气体

4. 理想气体状态方程的应用 (1)PV=nRT方程关联了四个物理量, 知其 中三个,可求第四个。 (2) 在特定条件下PV=nRT 可还原成 波义耳定律PV=常数 图 盖吕萨克定律V/T=常数 阿佛加德罗定律V/n=常数 履 P V/T=P2V2/T2 10
10 4.理想气体状态方程的应用 (1) PV = nRT方程关联了四个物理量, 知其 中三个,可求第四个。 (2) 在特定条件下 PV = nRT 可还原成 波义耳定律 PV = 常数 盖吕萨克定律 V / T = 常数 阿佛加德罗定律 V / n = 常数 P1V1 / T1 = P2V2 / T2