
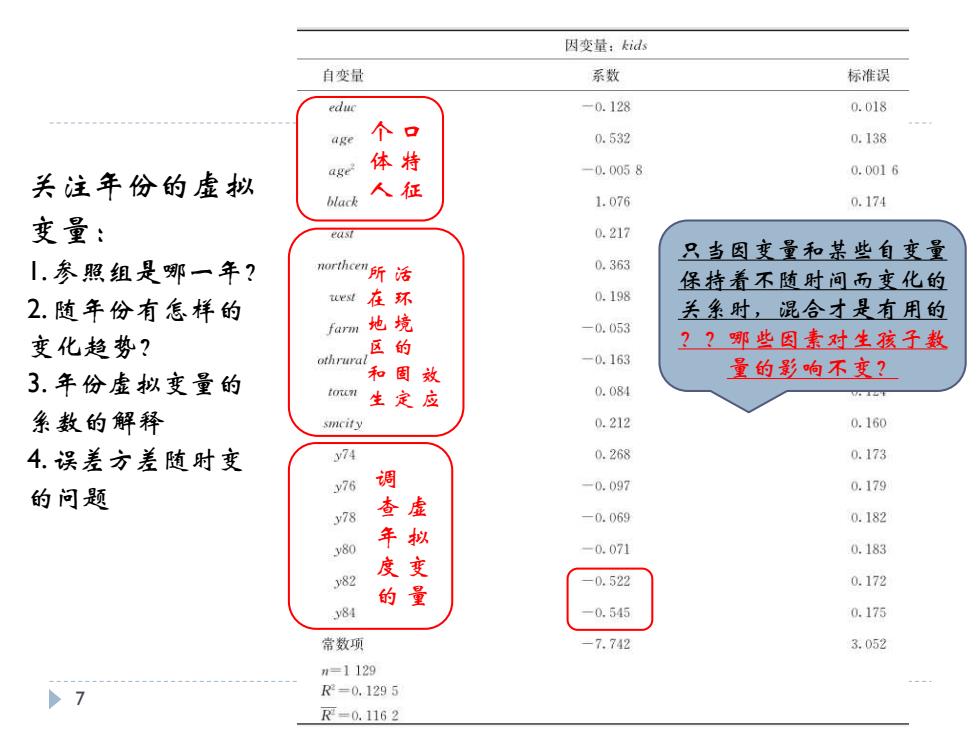
一、跨时独立横截面的混合 )例13.1不同时期的妇女生育率 FERTILI中的数据库[类似于桑德(Sander,I992)所用的数据库],来源于美国民意研究中心(Na tional Opinion Research Center)1972-1984年间的双数年(包括1972年和l984年)社会总调查(General Social Survey)。我们利用其中的数据来估计一个用以解释妇女生育小孩总数(kids)的模型。 一个令人感兴趣的问题是:在控制了其他可观测因素之后,这段时间里的生育率出现过什么变化?我们 所控制的因素是受教有年数、年龄、种族、16岁时生活的地区以及16岁时的生活环境。估计结果由表13-1 给出。 基年是1972年。年度虚拟变量的系数表明,在20世纪80年代早期生育率有一个明显下落。例如,y82 的系数意味着,在保持教育、年龄和其他因素不变的情况下,1982年和1972年相比,一位妇女平均少生育 0.52个孩子,或者说大约少半个孩子。这是一个很大的下跌:若保持教育、年龄和其他因素不变,在1982 年每100个妇女预计将比1972年同等条件的妇女少生育约52个小孩。因为我们控制了教育,这一下跌就和 因平均受教育程度的提高而导致的生育率下降没有联系。(1972年的平均受教育年数为12.2,而1984年为 13.3,)y82和y84代表解释变量所不能解释的生育率下降。 既然个别地看,1982年度和1984年度虚拟变量的系数都非常显著,那么多个年度虚拟变量构成的一组 变量也非常地联合显著就无足为奇了:不含年度虚拟变量的回归的R是0.1019,这就得到F111=5.87和 p值≈0。 6
一、跨时独立横截面的混合 例13.1 不同时期的妇女生育率 6
因变量:kids 自变量 系数 标准误 educ -0.128 0.018 age 个口 0.532 0.138 体特 -0.0058 0.0016 关注年份的虚拟 age black 人征 1.076 0.174 变量: east 0.217 只当因变量和某些自变量 1.参照组是哪一年? northceng所话 0.363 保持着不随时间而变化的 0.198 2.随年份有怎样的 ur在环 fam地境 关系时,混合才是有用的 -0.053 变化趋势? 区的 ??哪些因素对生孩子数 othrural -0.163 量的影响不变? 3.年份虚拟变量的 和固效 toun 生定应 0.084 系数的解释 smcity 0.212 0.160 4.误差方差随时变 y74 0.268 0.173 y76 调 的问题 -0.097 0.179 y78 查虚 -0.069 0.182 v80 年拟 -0.071 0.183 y82 度变 -0.522 的量 0.172 384 -0.545 0.175 常数项 7.742 3.052 n=1129 R=0.1295 F=0.1162
7 个体人 口特征 所在地区和生 活环境的固定 效应 调查年度的 虚拟变量 关注年份的虚拟 变量: 1. 参照组是哪一年? 2. 随年份有怎样的 变化趋势? 3. 年份虚拟变量的 系数的解释 4. 误差方差随时变 的问题 只当因变量和某些自变量 保持着不随时间而变化的 关系时,混合才是有用的 ??哪些因素对生孩子数 量的影响不变?

一、跨时独立横截面的混合 多受教育的妇女有较少的小孩,并且估计值是非常显著的。在其他条件不变的情况下,100名受大学教 育的妇女和100名仅受高中教育的妇女相比,生育的小孩要少约51个:0.128×4=0.512。年龄对生育有抑 制作用。(二次式的转折点在ag=46处。到了这个年龄,大多数妇女已停止生育小孩。) 表13-1中估计的模型假定每个解释变量(特别是受教育程度)的影响都保持不变。这一点正确与否, 尚不清楚;计算机练习C1要求你阐释这个问题。 最后,所估计方程的误差项中或许存在着异方差性。可利用第8章的方法来处理这个问题。但这里有 个有意思的区别:误差方差即使不随着educ、age、black等变量而变,还可能随时间而变。然而,异方差 稳健的标准误及其检验统计量仍是确当的。通过将OIS残差的平方对表13-1中的所有自变量(包括年度虚 拟变量)回归,就能得到布罗施-帕甘检验。(至于怀特统计量这个特殊情况,和平常一样,还要把拟合值 及其平方用作自变量。)加权最小二乘程序应能解决误差可能随时间而变的问题。在8.4节所讲的程序 中,还要把年度虚拟变量放到方程(8.32)中。 恩考题:如何考察某些变量的影响是否在某个 特定时期发生变化? 8
思考题:如何考察某些变量的影响是否在某个 特定时期发生变化? 一、跨时独立横截面的混合 8

一、 跨时独立横截面的混合 例13.2教育回报和工资中性别差异的变化 将1978年(基年)和1985年的横截面数据相混合,得到log(ag)的一个方程(其中age为小时工 资)是 log(uge)=3十 %3y85 +B:union3feale y85·female (13.1) 其中大多数解释变量,我们现在应该都已经熟悉。变量0m(工会)是个虚拟变量:如果某人是工会会 员,它就等于1,否则等于0。变量85也是一个虚拟变量;如果观测值来自1985年就等于1,如果来自 1978年就等于0。在1978年的样本中有550人,而在1985年则是另一组不同的534人。 1978年的裁距是B,而1985年的截距是B,十6,。1978年的教育回报是3,而1985年的教育回报是3十 1。因此,度量了多受一年教育获得的回报经过7年时间以后所发生的变化。最后,男女对数工资的差别 在1978年是B;在1985年是房十d。于是,通过检验H:6=0,就能检验性别差异在这7年里没有变化 的原假设。表示性别差异·已减少的备择假设则是H:>0。为简单起见,我们假定工作经验和工会会员 资格在两个时期里对工资都有同样的影响。 9
一、跨时独立横截面的混合 9 例13.2 教育回报和工资中性别差异的变化

一、跨时独立横截面的混合 倒13.2教育回报和工资中性别差异的变化-续)e1C奇的回归年 现在我们用CPS78_85中的数据来估计方程式 数怎样解释? log(uge)=0.459+0.118y85+ 0.0747edu 0.0185y85·cdu 3.educ与年份交互 (0.093)(0.124) t0.009t分 +0.0296 ex per-0.00040 er per2+0.202ion 项的回归象数如何 (0.0036) (0.00008) (0.030) 解释? (13.2) -0.317 female+0.085y85.female (0.037)(0.051) 4.教育回报在不同 n=1084,R=0.426,R2=0.422 时期有变化吗? 1978年的教育回报估计约为7.5%;1985年的教育回报约为9.35%,即高出了1.85个百分点。由于交互项 的1统计量为0.0185/0.0094≈1.97,在双侧备择假设下,教育回报的差异在5%的水平上统计显著。 性别差异怎么样呢?在1978年,其他条件相同的妇女工资比男性工资约少31,7%(更准确的估计是 27.2%)。到1985年,log(xage)的差别是(-0.317)十0.085=-0.232。因此,性别差异(从1978年到 1985年)已降低了8.5个百分点。交互项的1统计量约为1.67,这意味着相对于为正的单侧备择假设来 说,它在5%的水平上显著。 10
例13.2 教育回报和工资中性别差异的变化-续 一、跨时独立横截面的混合 10 1. 参照组是哪一年? 2. educ前的回归系 数怎样解释? 3. educ与年份交互 项的回归系数如何 解释? 4. 教育回报在不同 时期有变化吗?