
Financial Econometrics Chapter 2.Statistical Foundations:Overview of OLS Jin Ling School of Finance,Zhongnan University of Economics and Law
Financial Econometrics Chapter 2. Statistical Foundations: Overview of OLS Jin Ling School of Finance, Zhongnan University of Economics and Law 1

Outline Statistical Foundation Review ·Overview of OLS ·Practice of OLS 2
• Statistical Foundation Review • Overview of OLS • Practice of OLS 2 Outline

Statistical Foundation Review ·Probability: P(AB)=P(AnB) 么B为相互独立的随机事件。此时,P48)=P4=PA,故 P(B) P(B) P(A0B)=P(A)P(B) B AnB P(0=∑,P(B,)P(AB) 图2.1条件概率示意图 3
• Probability: 3 Statistical Foundation Review

Statistical Foundation Review Defination of random variable: The conditional value. Probability distribution:Discrete distribution,continuous distribution,joint distribution: ①fxy≥0,xy: Xxx2.装. 间∫f.)dxdy=1: p乃P2.Pk. (曲(x,门落入平面某区域D的概率为P{(x,门eD)=川/x)d山. 连续型随机变量可以取任意实数,其“概率密度函数”(probability density function,简记 d山f)满足, 从二维联合密度函数f(x,),可以计算X的(一维)边缘密度函数(marginal pd的: ①fx)≥0,x: f)-∫"fx (2.6) 间∫f)c=1 这个公式的直观含义与“全概率公式”相似,即给定x,把所有y取值的可能性都“加”起 (G间x落入区间[a,]的概率为P代a《Xs)=∫广f)d, 来(积分的本质就是加总),类似地,可以计算Y的(一维)边缘密度函数: 2.7) 定义“累积分布函数”(cumulative distribution function,简记cd的为 f09=J.f红)d F国)=m<X≤=广f0d 2.5) 定义二维随机向量(X,门的累积分布函数为 其中,1为积分变量。直观来看,下()度量的是,从-至x为止,概念密度函数f)曲线 Fx,川=P-m<X<g-o<y<》=广∫f化,)出山 2.8 下的面积
• Defination of random variable: • The conditional value. • Probability distribution: Discrete distribution, continuous distribution, joint distribution: 4 Statistical Foundation Review
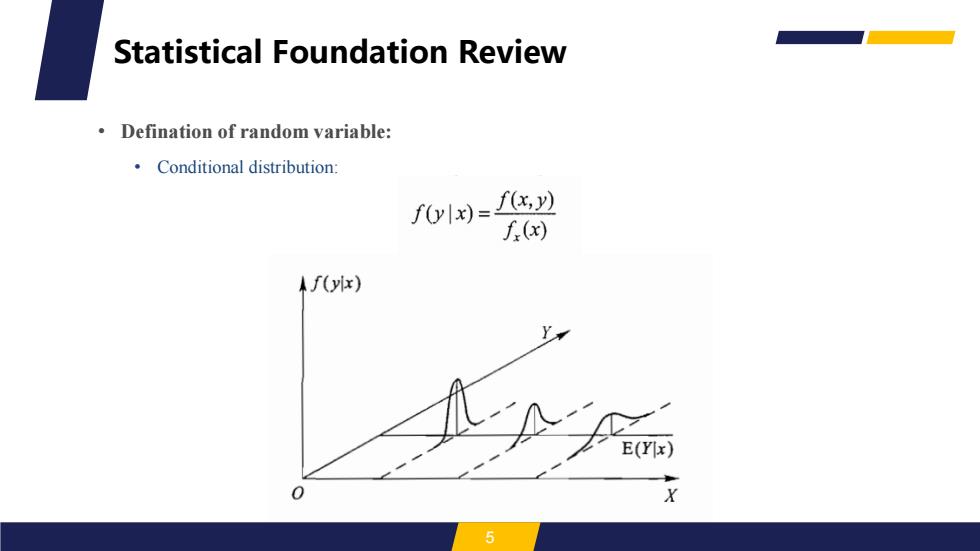
Statistical Foundation Review Defination of random variable: Conditional distribution: flx)= (x) Af(yix) E(Yix) X 5
• Defination of random variable: • Conditional distribution: 5 Statistical Foundation Review