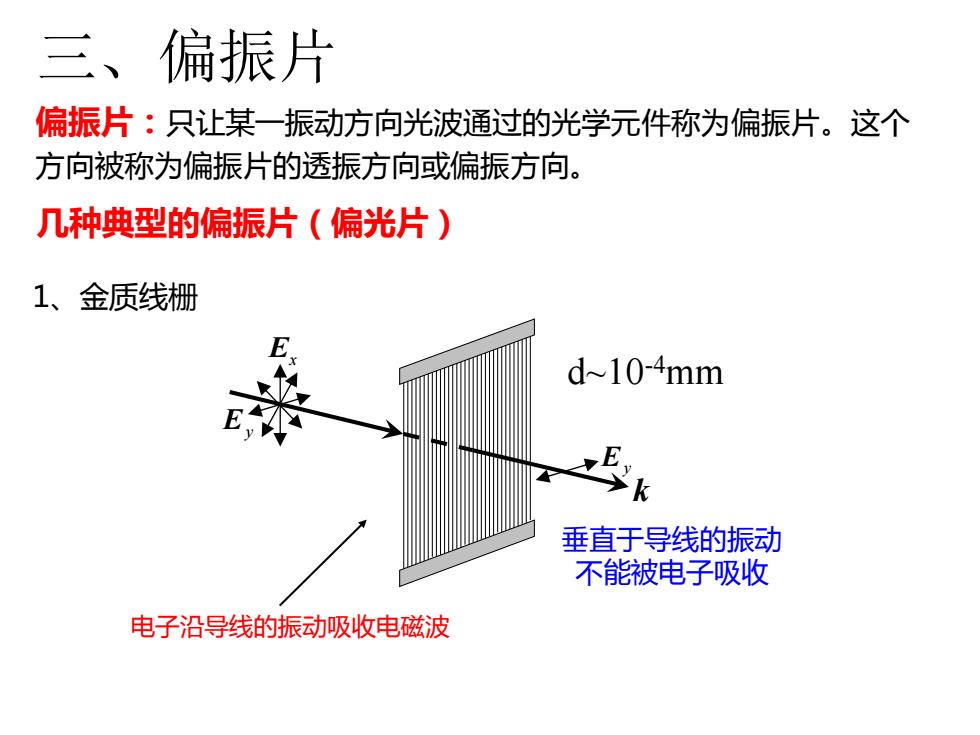
三、偏振片 偏振片:只让某一振动方向光波通过的光学元件称为偏振片。这个 方向被称为偏振片的透振方向或偏振方向。 几种典型的偏振片(偏光片) 1、金质线栅 d~10-4mm 垂直于导线的振动 不能被电子吸收 电子沿导线的振动吸收电磁波
三、偏振片 几种典型的偏振片(偏光片) 1、金质线栅 k E x E y E y d~10-4mm 垂直于导线的振动 不能被电子吸收 电子沿导线的振动吸收电磁波 偏振片:只让某一振动方向光波通过的光学元件称为偏振片。这个 方向被称为偏振片的透振方向或偏振方向

2、人造偏振片一二向色性偏振片 包括J、H、K等类型的人造偏振片 H偏振片(E.H.Land,1938) ① 聚烯醇薄膜基片; ②在蒸汽中均匀加热拉伸,使长键分子整齐排列; ③浸碘,使碘分子聚合到已被拉直的分子链上; ④ 干燥后,形成导电的碘链 ⑤ 称为性能优良的偏振片 Edwin Herbert Land 优点:偏振度高达99%以上,可用于整个可见光 (1909≈1991) 波段,是目前使用最广泛的人造偏振片 1928年首次通过机械挤 压制造了型偏振片。 缺点:强度差,不能受潮,易退偏
2、人造偏振片—二向色性偏振片 ① 聚烯醇薄膜基片; ② 在蒸汽中均匀加热拉伸,使长键分子整齐排列; ③ 浸碘,使碘分子聚合到已被拉直的分子链上; ④ 干燥后,形成导电的碘链 ⑤ 称为性能优良的偏振片 Edwin Herbert Land (1909~1991 ) 优点:偏振度高达99%以上,可用于整个可见光 波段,是目前使用最广泛的人造偏振片 缺点:强度差,不能受潮,易退偏。 H偏振片(E. H. Land ,1938) 包括J、H、K等类型的人造偏振片 1928年首次通过机械挤 压制造了J型偏振片
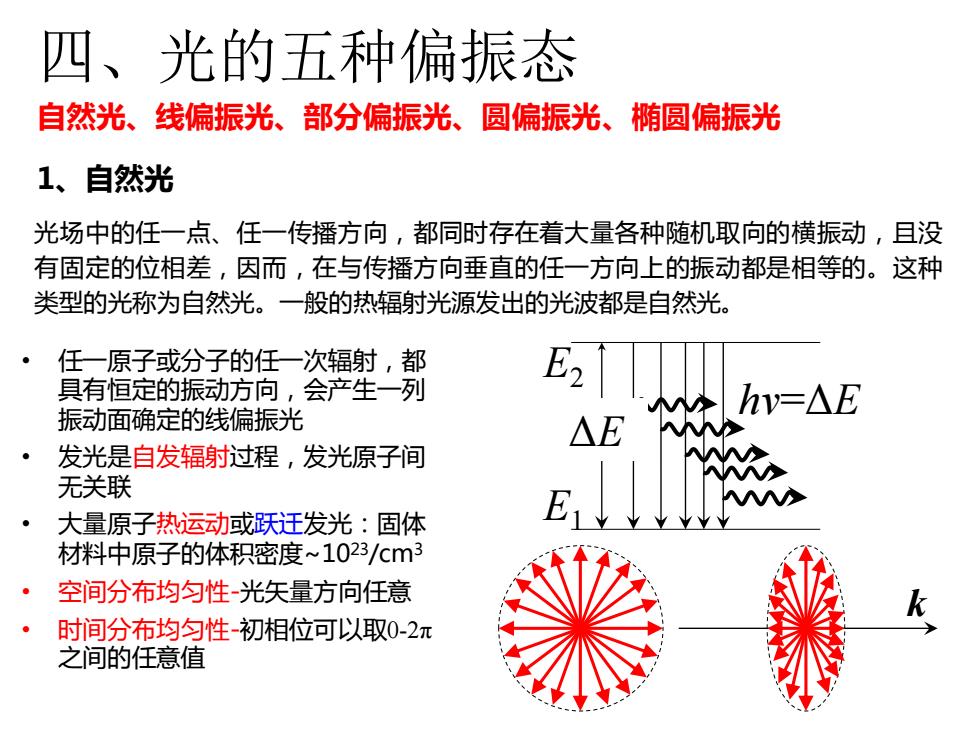
四、光的五种偏振态 自然光、线偏振光、部分偏振光、圆偏振光、椭圆偏振光 1、自然光 光场中的任一点、任一传播方向,都同时存在着大量各种随机取向的横振动,且没 有固定的位相差,因而,在与传播方向垂直的任一方向上的振动都是相等的。这种 类型的光称为自然光。一般的热辐射光源发出的光波都是自然光。 任一原子或分子的任一次辐射,都 具有恒定的振动方向,会产生一列 E2 hv=△E 振动面确定的线偏振光 △E 发光是自发辐射过程,发光原子间 无关联 大量原子热运动或跃迁发光:固体 材料中原子的体积密度~1023/cm3 空间分布均匀性-光矢量方向任意 时间分布均匀性-初相位可以取0-2π 之间的任意值
四、光的五种偏振态 1、自然光 光场中的任一点、任一传播方向,都同时存在着大量各种随机取向的横振动,且没 有固定的位相差,因而,在与传播方向垂直的任一方向上的振动都是相等的。这种 类型的光称为自然光。一般的热辐射光源发出的光波都是自然光。 • 任一原子或分子的任一次辐射,都 具有恒定的振动方向,会产生一列 振动面确定的线偏振光 • 发光是自发辐射过程,发光原子间 无关联 • 大量原子热运动或跃迁发光:固体 材料中原子的体积密度~1023/cm3 • 空间分布均匀性-光矢量方向任意 • 时间分布均匀性-初相位可以取0-2π 之间的任意值 E2 E1 hν=ΔE ΔE k 自然光、线偏振光、部分偏振光、圆偏振光、椭圆偏振光
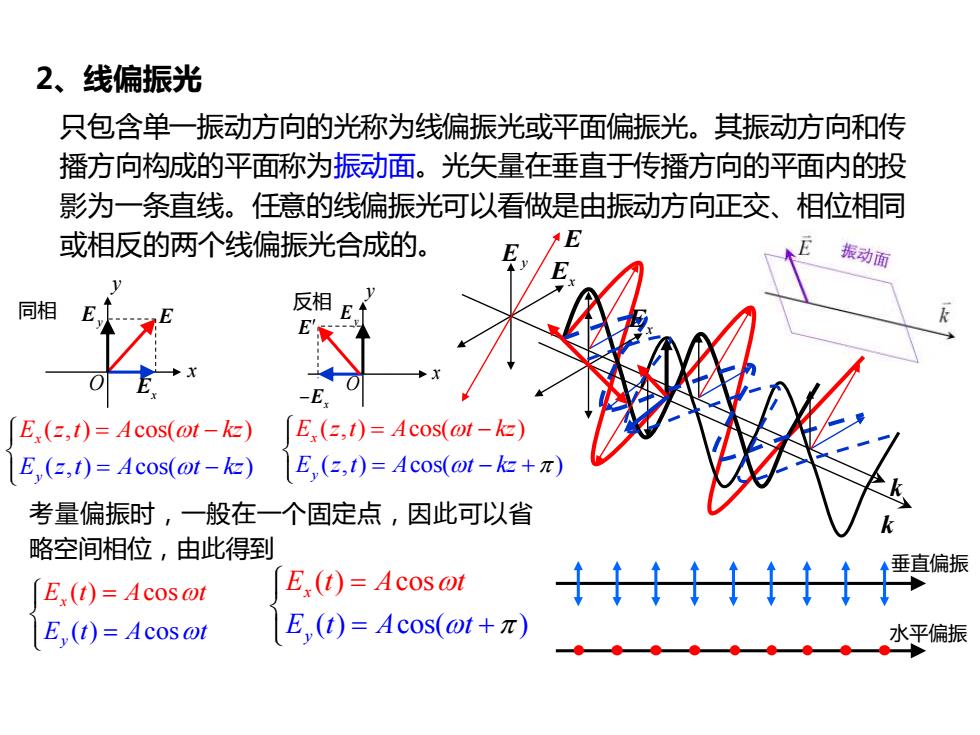
2、线偏振光 只包含单一振动方向的光称为线偏振光或平面偏振光。其振动方向和传 播方向构成的平面称为振动面。光矢量在垂直于传播方向的平面内的投 影为一条直线。任意的线偏振光可以看做是由振动方向正交、相位相同 或相反的两个线偏振光合成的。 振动面 同相 反相 E,(=,t)=Acos(ot-k) E,(,1)=Acos(ot-k) E,(=,1)=Acos(ot-k) E,(,t)=Acos(@t-kz+) 考量偏振时,一般在一个固定点,因此可以省 略空间相位,由此得到 E,(t)=Acos@t E,(t)=Acosot 十十十于十十1十真碳 E(t)=Acos@t E,(t)=Acos(ot+π) 水平偏振
2、线偏振光 只包含单一振动方向的光称为线偏振光或平面偏振光。其振动方向和传 播方向构成的平面称为振动面。光矢量在垂直于传播方向的平面内的投 影为一条直线。任意的线偏振光可以看做是由振动方向正交、相位相同 或相反的两个线偏振光合成的。 E E x E y x y O 垂直偏振 水平偏振 反相 k E E x E y k E x ( , ) cos( ( , ) cos( ) ) x E z t A t kz y E z t A t kz = − = − + ( ( , ) cos( , ) cos( ) ) x E z y E z t t A t A t k kz z = − = − E −E x E y x y O 同相 考量偏振时,一般在一个固定点,因此可以省 略空间相位,由此得到 ( ( ) co ) cos s y x E t E t t A t A = = ( ) ( ) c s( ) os co y E t A t x E t A t = + =