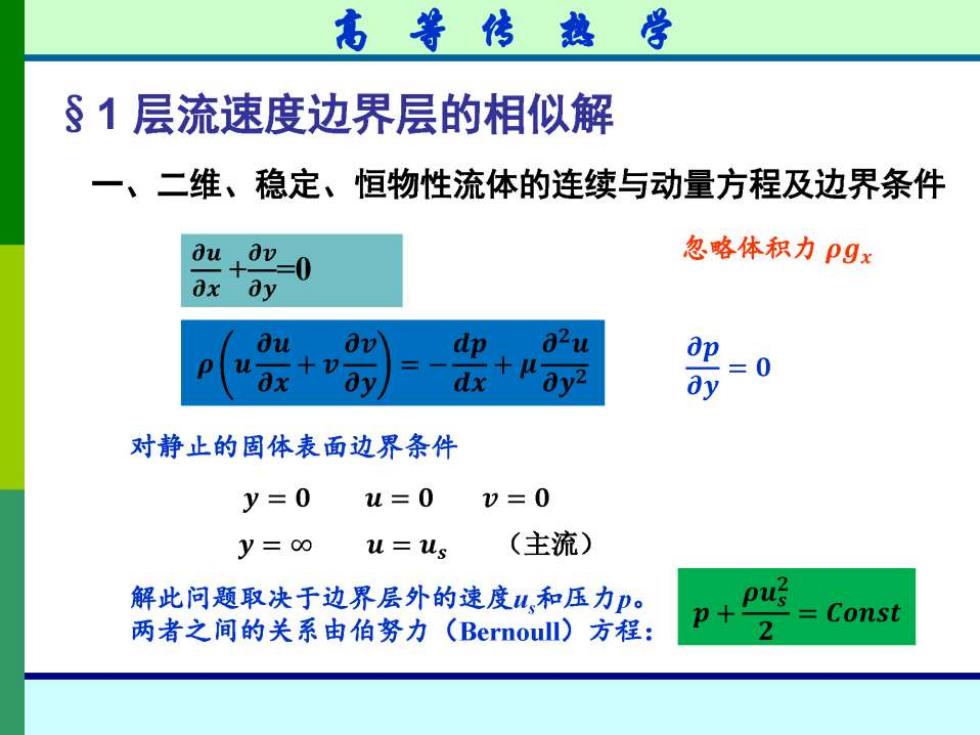
高等传热学 §1层流速度边界层的相似解 二维、稳定、恒物性流体的连续与动量方程及边界条件 du 0v0 忽略体积力pgx ax dy Bu av dp 82u + 0x dx ∂v2 2=0 对静止的固体表面边界条件 y=0 u=0 0=0 y=0∞ u=us (主流) 解此问题取决于边界层外的速度山,和压力p。 pus p+ =Const 两者之间的关系由伯努力(Bernoull).方程:
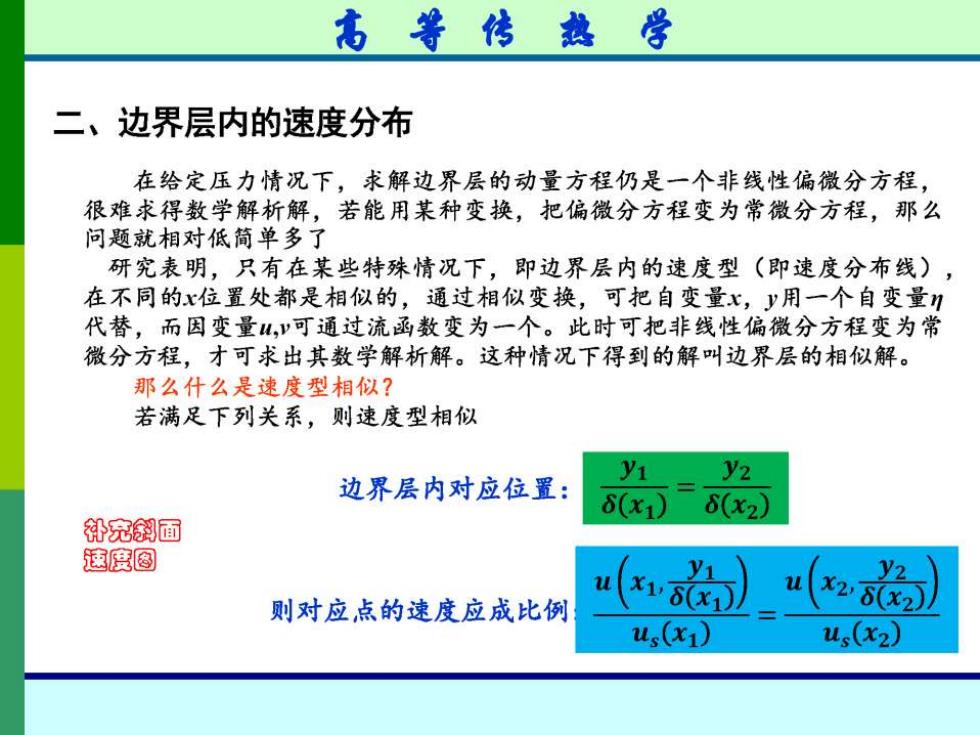
高等传热学 二、边界层内的速度分布 在给定压力情况下,求解边界层的动量方程仍是一个非线性偏微分方程, 很难求得数学解析解,若能用某种变换,把偏微分方程变为常微分方程,那么 问题就相对低简单多了 研究表明,只有在某些特殊情况下,即边界层内的速度型(即速度分布线), 在不同的x位置处都是相似的,通过相似变换,可把自变量x,y用一个自变量? 代替,而因变量山,可通过流函数变为一个。此时可把非线性偏微分方程变为常 微分方程,才可求出其数学解析解。这种情况下得到的解叫边界层的相似解。 那么什么是速度型相似? 若满足下列关系,则速度型相似 y2 边界层内对应位置: 6(x1) 6(x2) 补充斜面 速度图 y2 则对应,点的速度应成比例 X18x1 x28x2 us(x1) u,x2】
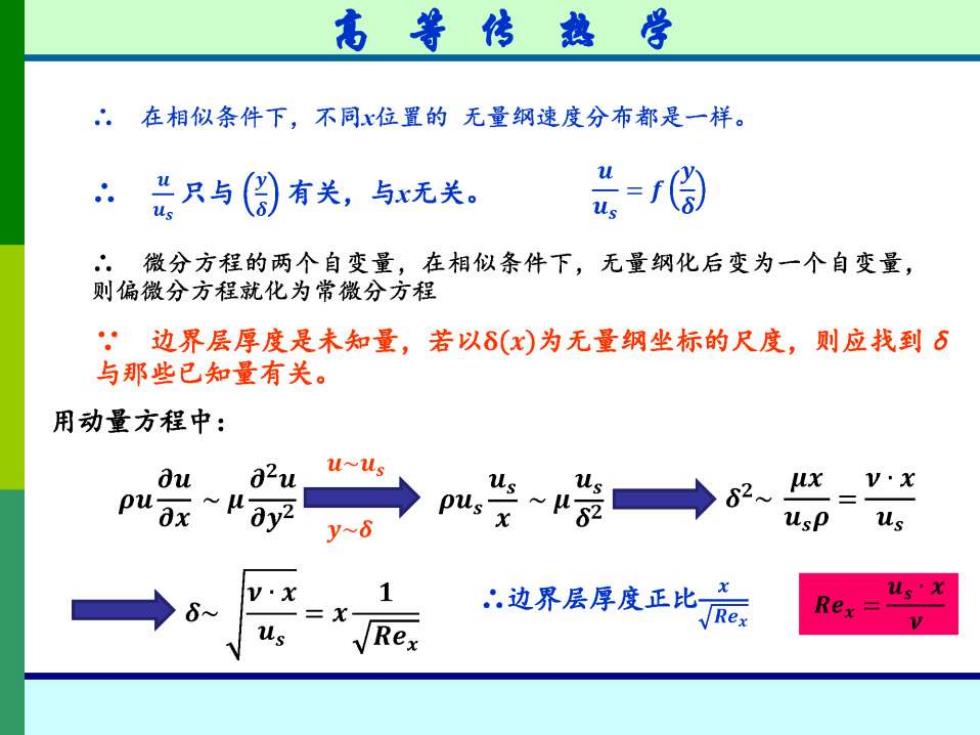
高等传热学 ∴在相似条件下,不同x位置的无量纲速度分布都是一样。 “只与 有关,与x无关。 u us .微分方程的两个自变量,在相似条件下,无量纲化后变为一个自变量, 则偏微分方程就化为常微分方程 :边界层厚度是未知量,若以⑧(x)为无量纲坐标的尺度,则应找到6 与那些已知量有关。 用动量方程中: ou 82u u~us pu 82 0x ~μay2 y~6 usP us V·x “边界层厚度正比心 us'x Rex us Rex

高等传热学 现在讨论在什么样情况下边界层内速度型相似呢? 1930年由法尔克纳-斯肯等作出研究结果,由相似变换得出,若山 按如下形式变化us=Cxm,则速度型相似。 而流体绕流楔型物体时,就具有us=Cxm的速度型,因而流体绕 流楔型物体时,其速度型相似。 式中C为常数,m~楔型物体张角有关,由流体力学知: m=品。支B= m+1 y 引入相似变量: 6(x) 考虑m的影响,即不同张角的情况,令: m+1y 1= 2 Rex 则是考的函数,即是n的函数,fm)=兴d us
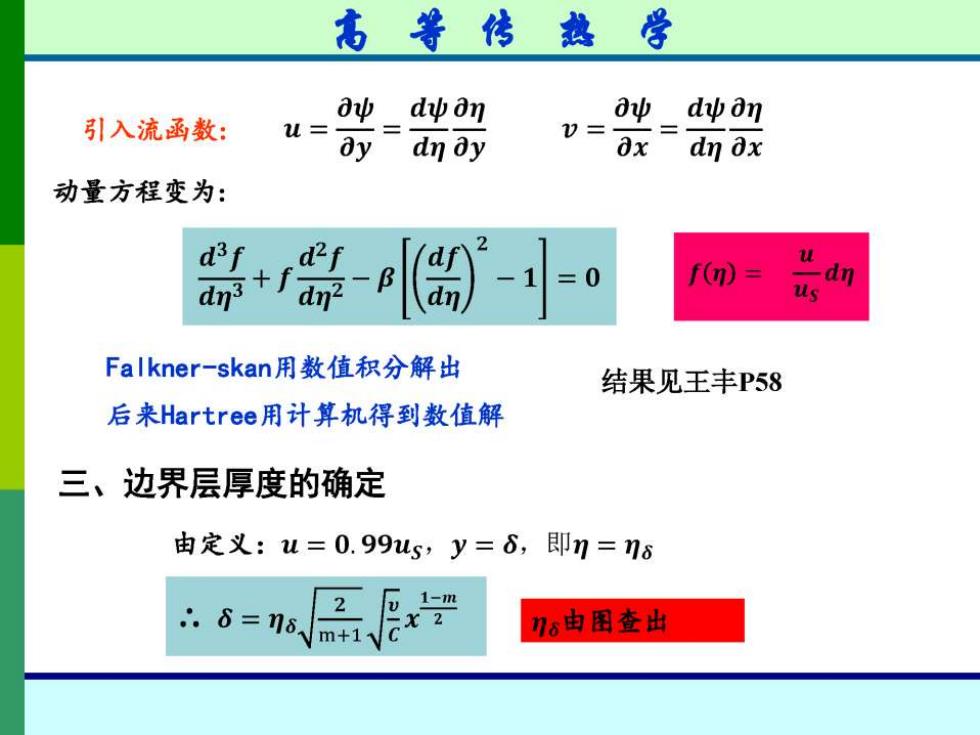
高等传热学 ∂ψ 引入流函数: dψan aψdψan u= 0= ay dn ay ∂xdn∂x 动量方程变为: d-f :0 dn dn3 dn2 us Falkner-skan用数值积分解出 结果见王丰P58 后来Hartree用计算机得到数值解 三、边界层厚度的确定 由定义:u=0.99us,y=6,即n=1s 2 1-m m+1, X 2 76由图查出