
§1.2矩阵的广义逆 一、减号逆 定义1.2.1设A为n×p阶矩阵,若存在一个 p×n阶矩阵X,使得AXA=A,则称X为A 的广义逆或A的减号逆,记作X=A. 11
11 §1.2 矩阵的广义逆 . 1 . 2 . 1 − = × = × A X A p n X AXA A X A A n p 的广义逆或 的减号逆,记作 阶矩阵 ,使得 ,则称 为 定义 设 为 阶矩阵,若存在一个 一、减号逆

性质1任何矩阵的广义逆一定存 在,但可能不唯一。 12
12 性质1 任何矩阵的广义逆一定存 在,但可能不唯一

证明:设rank(A)=r,A可分解为 nX p 0 0 其中P和Q分别为n和p非奇异方阵,于是有 AXA=A→ 0) 0 13
13 Q I Q P I QXP I P AXA A P Q n p Q I A P rank A r A r r r r n p ⎟⎟⎠⎞ ⎜⎜⎝⎛ = ⎟⎟⎠⎞ ⎜⎜⎝⎛ ⎟⎟⎠⎞ ⎜⎜⎝⎛ = ⇔ ⎟⎟⎠⎞ ⎜⎜⎝⎛ = = × 0 0 0 0 0 0 0 0 0 0 0 0 : ( ) 其中 和 分别为 和 阶非奇异方阵,于是有 证明 设 , 可分解为
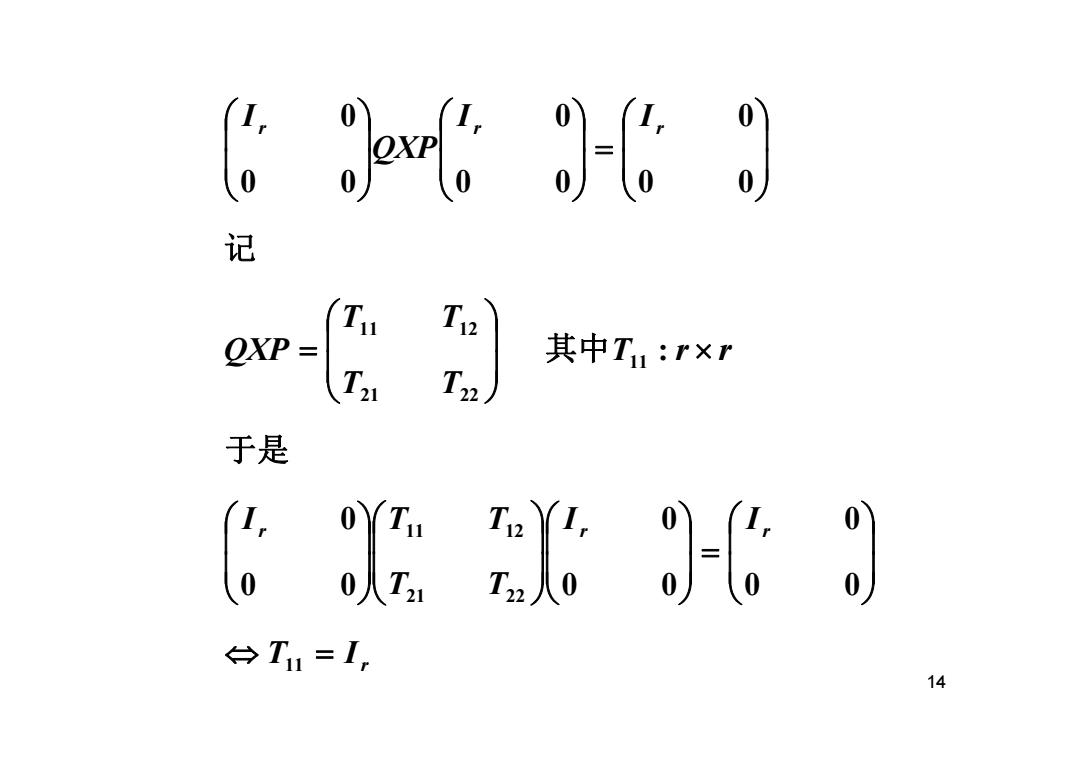
g取t 0 0 记 Tr OXP= 其中Tu:r×r T2 T2) 于是 G斯& 0 台T1=, 14
14 r r r r r r r T I I I T T I T T T r r T T T T QXP I I QXP I ⇔ = ⎟⎟⎠⎞ ⎜⎜⎝⎛ =⎟⎟⎠⎞ ⎜⎜⎝⎛⎟⎟⎠⎞ ⎜⎜⎝⎛⎟⎟⎠⎞ ⎜⎜⎝⎛ × ⎟⎟⎠⎞ ⎜⎜⎝⎛ = ⎟⎟⎠⎞ ⎜⎜⎝⎛ =⎟⎟⎠⎞ ⎜⎜⎝⎛ ⎟⎟⎠⎞ ⎜⎜⎝⎛ 11 21 22 11 12 11 21 22 11 12 0 0 0 0 0 0 0 0 0 : 0 0 0 0 0 0 0 0 0 于是 其中 记

1 Tr 所以QXP= T 即X=Q P-1 其中T12,T1T2可任意选择,X就是A的广义逆A, 这表明A一定存在,但可能不唯一. 15
15 . 12 21 22 1 21 22 12 1 21 22 12 这表明 一定存在,但可能不唯一 其中 , , 可任意选择, 就是 的广义逆 , 即 所以 − − − − ⎟⎟⎠⎞ ⎜⎜⎝⎛ = ⎟⎟⎠⎞ ⎜⎜⎝⎛ = A T T T X A A P T T I T X Q T T I T QXP r r