
第六章方差分析 (第2部分) 第二节单因素试验资料的方差分析
第六章 方差分析 (第2部分) 第二节 单因素试验资料的方差分析
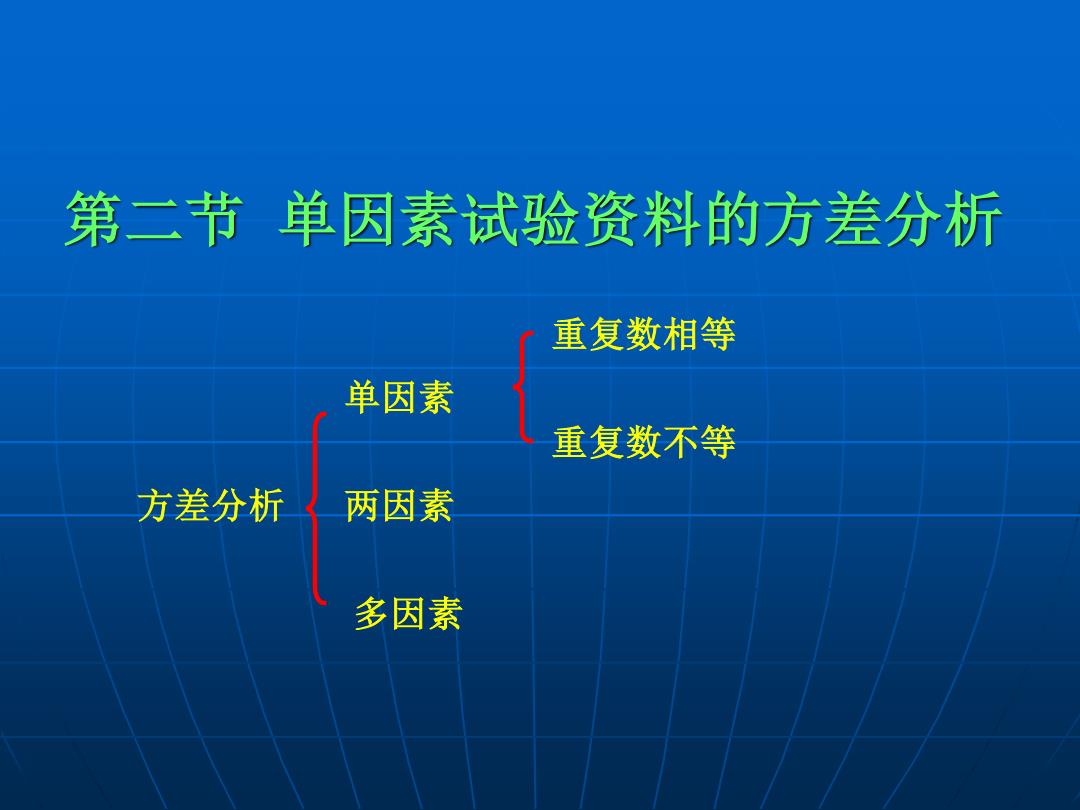
第二节单因素试验资料的方差分析 重复数相等 单因素 重复数不等 方差分析 两因素 多因素
第二节 单因素试验资料的方差分析 方差分析 单因素 多因素 两因素 重复数相等 重复数不等
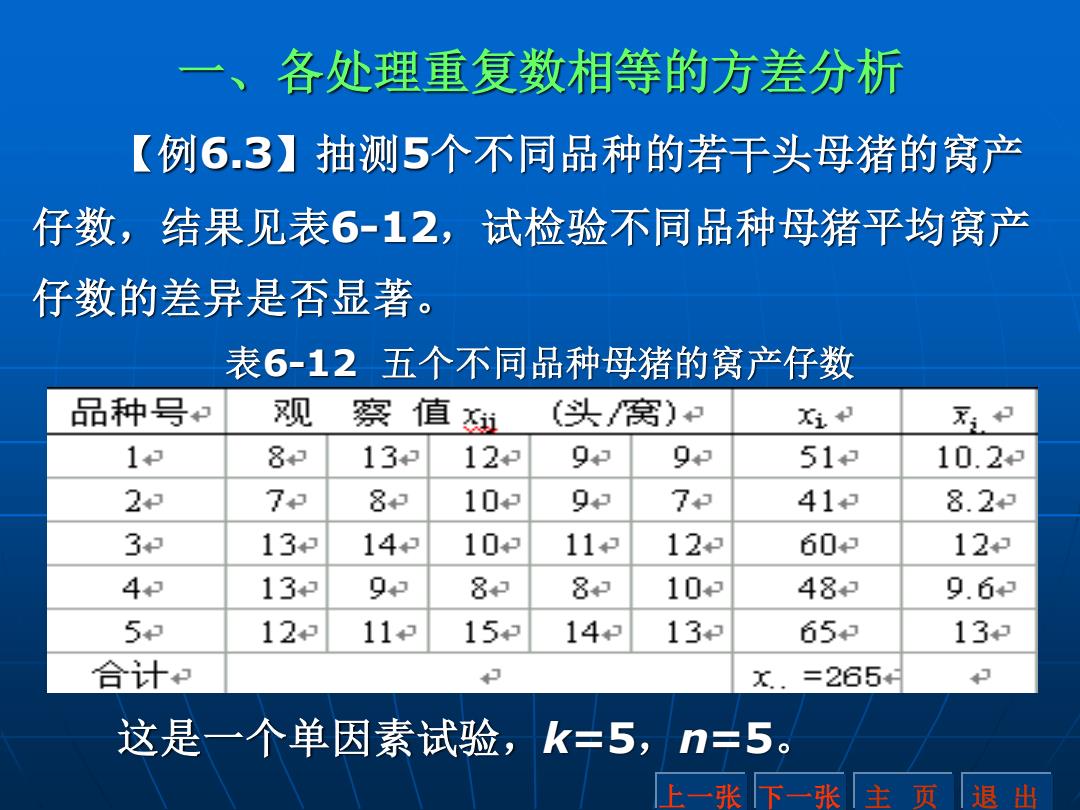
各处理重复数相等的方差分析 【例6.3】抽测5个不同品种的若干头母猪的窝产 仔数, 结果见表6-12,试检验不同品种母猪平均窝产 仔数的差异是否显著 表6-12五个不同品种母猪的窝产仔数 品种号和 观 察值斑 (头窝) Xi. 1 8 13 12 93 9 51 10.22 2 7 82 10 9 7 41 8.2 3 13 14 10 11 12 602 12 43 13 92 82 8 102 483 9.62 5 12 11 15 14 13 65 13 合计 x.=265 这是一个单因素试验,k=5,n=5。 上一张 下一张主页 退出
一、各处理重复数相等的方差分析 【例6.3】抽测5个不同品种的若干头母猪的窝产 仔数,结果见表6-12,试检验不同品种母猪平均窝产 仔数的差异是否显著。 表6-12 五个不同品种母猪的窝产仔数 上一张 下一张 主 页 退 出 这是一个单因素试验,k=5,n=5

1、计算各项平方和与自由度 C=x2/kn=2652/(5×5)=2809.00 SS7=∑∑x-C=(82+132++142+132)-2809.00 =2945.00-2809.00=136.00 S8=号∑x-C=号(51+41P+602+482+65)-2809.0 =2882.20-2809.00=73.20 SS。=SS,-SS,=136.00-73.20=62.80 df=kn-1=5×5-1=24 f=k-1=5-1=4 df。=fr-dj,=24-4=20 上一张下一张主页退出
1、计算各项平方和与自由度 / 265 /(5 5) 2809.00 2 2 C = x.. k n= = 2945.00 2809.00 136.00 (8 13 14 13 ) 2809.00 2 2 2 2 2 = − = SST =xi j −C = + ++ + − 上一张 下一张 主 页 退 出 2882.20 2809.00 73.20 (51 41 60 48 65 ) 2809.00 5 1 2 1 2 2 2 2 2 . = − = = x −C = + + + + − n SSt i SSe = SST − SSt =136.00−73.20 = 62.80 dfT = k n−1= 55−1= 24 dft = k −1= 5−1= 4 dfe = dfT − dft = 24− 4 = 20
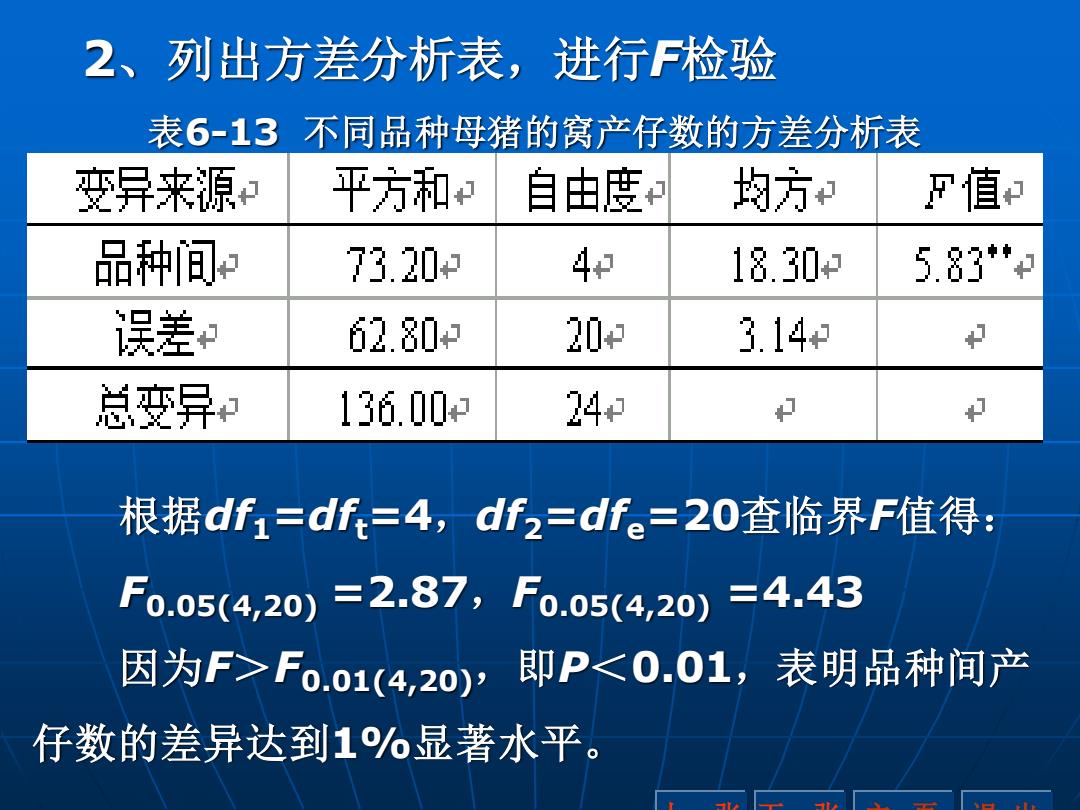
2、列出方差分析表,进行F检验 表6-13不同品种母猪的窝产仔数的方差分析表 变异来源和 平方和和 自由度蜘 均方中 F值和 品种间 73.20 4和 18.30 5.83*+ 误差 62.80 20+ 3.14 总变异+ 136.00 24 中 根据df1=df=4,df2=df。=20查临界F值得: F0.5(4,20)=2.87,F0.05(4,20)=4.43 因为F>F0.o1(4,20),即P<0.01,表明品种间产 仔数的差异达到1%显著水平
2、列出方差分析表,进行F检验 表6-13 不同品种母猪的窝产仔数的方差分析表 上一张 下一张 主 页 退 出 根据df1=dft=4,df2=dfe=20查临界F值得: F0.05(4,20) =2.87,F0.05(4,20) =4.43 因为F>F0.01(4,20),即P<0.01,表明品种间产 仔数的差异达到1%显著水平