
第四章分子对称性 分子的对称操作与对称元素 对称操作:旋转 对称操作:不改变图 对称元素:旋转轴 形中任何两点的距离而能 使图形复原的操作叫做对 称操作 对称操作据以进行的几何 要素(点,面和线)叫做 对称元素
对称操作:不改变图 形中任何两点的距离而能 使图形复原的操作叫做对 称操作 分子的对称操作与对称元素 对称元素: 旋转轴 对称操作: 旋转 第四章 分子对称性 对称操作据以进行的几何 要素(点,面和线)叫做 对称元素

分子中的四类对称操作及相应的对称元素如下. 1. 恒等元素E 恒等操作E 2. 对称轴Cn 旋转操作Cn 单重轴C10(转角)=2m 二重轴C20(转角)=π 3. 对称面(σ) 反应操作(σ) 4. 对称中心(i) 反演操作(i) 5. 象转轴(Sn) 旋转反映操作(Sn)
7 分子中的四类对称操作及相应的对称元素如下: 1. 恒等元素E 恒等操作E 2. 对称轴Cn 旋转操作Cn 单重轴C1 θ(转角)=2π 二重轴C2 θ(转角)=π 3. 对称面(σ) 反应操作(σ) 4. 对称中心(i) 反演操作(i) 5. 象转轴(Sn) 旋转反映操作(Sn)
第四章分子对称性 旋转轴与旋转操作 分子中若存在一条轴线,绕此轴旋转一定角度能使 分子复原,就称此轴为旋转轴,符号为C,·旋转可以实际 进行,为真操作;相应地,旋转轴也称为真轴。 H202中的C 202 (旋转轴上的椭圆形为C的图形符号。类似地,正三角形、正方形、正六边 形分别是C3、C和C6的图形符号)
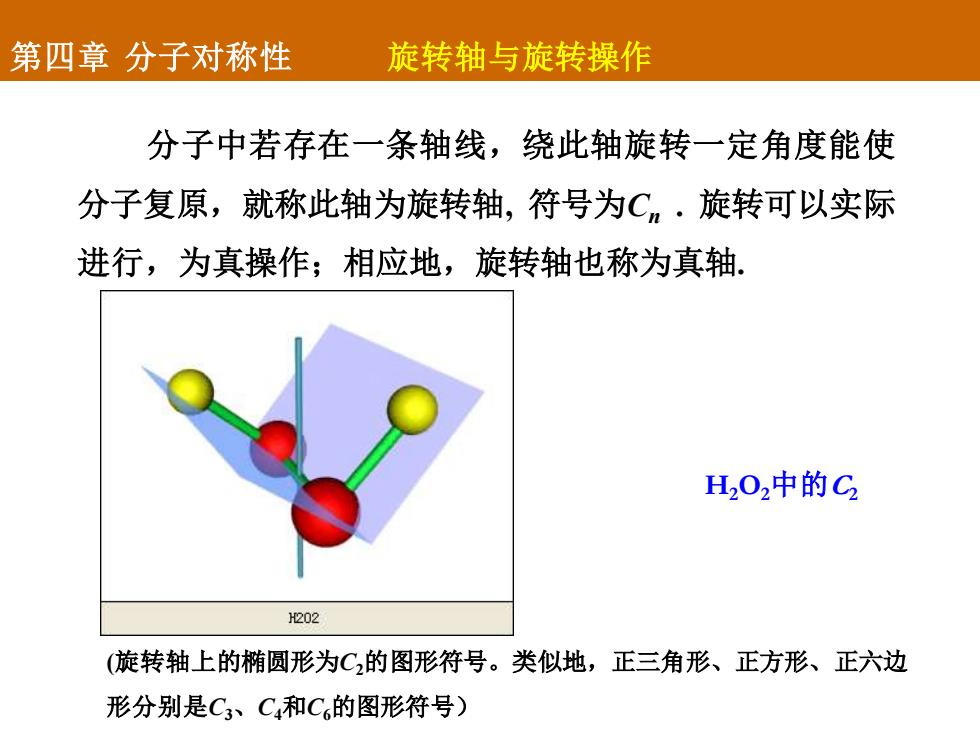
分子中若存在一条轴线,绕此轴旋转一定角度能使 分子复原,就称此轴为旋转轴, 符号为Cn . 旋转可以实际 进行,为真操作;相应地,旋转轴也称为真轴. H2O2中的C2 (旋转轴上的椭圆形为C2的图形符号。类似地,正三角形、正方形、正六边 形分别是C3、C4和C6的图形符号) 第四章 分子对称性 旋转轴与旋转操作

第四章分子对称性 旋转轴与旋转操作 轴定义 将分子图形以直线为轴旋转某个角度能产生 分子的等价图形。 单重(次)轴(C1)0=2π 二重(次)轴(C2)日=2列 三重(次)轴(C)8=2π分 : n重(次)轴(Cm)0=2π 操作定义 旋转轴能生成n个旋转操作,记为:
将分子图形以直线为轴旋转某个角度能产生 分子的等价图形。 操作定义 旋转轴能生成n个旋转操作,记为: . ( ) 二重(次)轴 C2 2 q = 2p 单重(次)轴 (C1 ) q = 2p 三重(次)轴 3 (C3 ) q = 2p n重(次)轴 n (C n ) q = 2p , Cn , 1 − C n n , 2 Cn C = E n n . . Cn轴定义 第四章 分子对称性 旋转轴与旋转操作
第四章分子对称性 (1)旋转轴与旋转操作 CHFCIBr 10
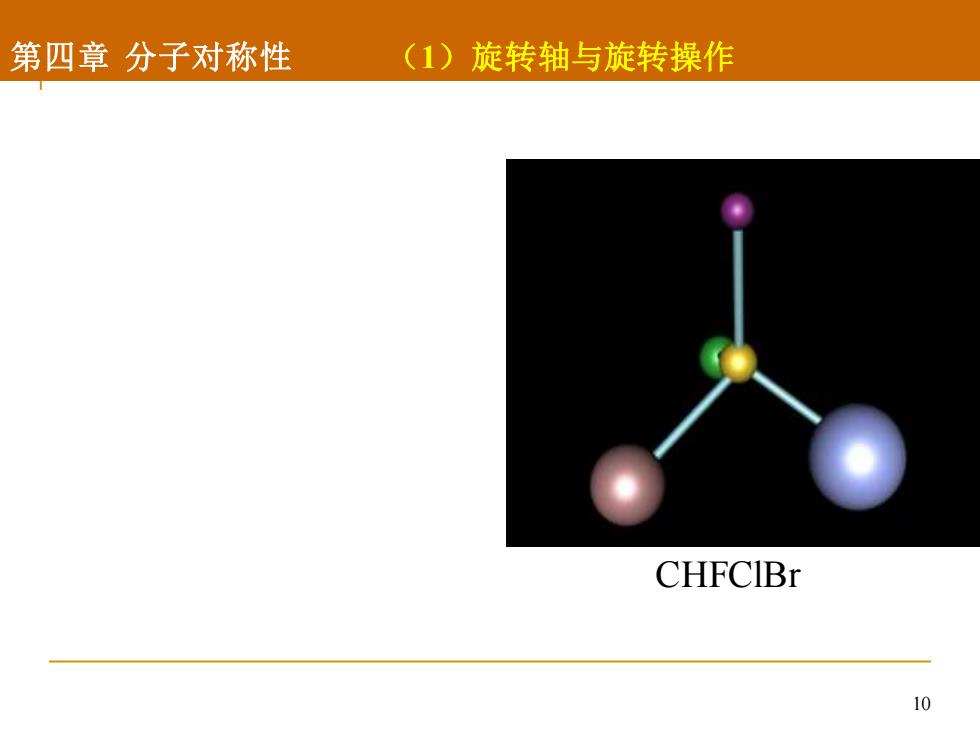
10 第四章 分子对称性 (1)旋转轴与旋转操作 CHFClBr