
第二部分,结构化学实验 实验一磁化率的测定 一、实验目的 1.掌握古埃Gouy)法测定磁化率的原理和方法。 2.测定三种络合物的磁化率,求算未成对电子数,判断其配键类型。 3.了解磁天平的原理与测定方法。 二、基本原理 1磁化率:物质在外磁场中,会被磁化并感生一附加磁场,其磁场强度H'与外磁场强 度H之和称为该物质的磁感应强度B,即 B=H+H' 1 H'与H方向相同的叫顺磁性物质,相反的叫反慰性物质。还有一类物质如铁、钻、及其 合金,H 比H 大得多(H'H)高达10,而且附加磁场在外磁场消失后并不立即消失,这 类物质称为铁磁性物质。物质的磁化可用磁化强度1来描述,H'=4。对于非铁磁性物质, 1与外磁场强度H成正比 I=KH 121 式中,《为物质的单位体积磁化率(简称磁化率),是物质的一种宏观磁性质。在化学中常用 单位质量磁化率X或摩尔磁化率表示物质的磁性质,它的定义是 Xm=K/p 9 XM MK/p 4 式中,P和M分别是物质的密度和摩尔质量。由于K是无量纲的量,所以Xm和m的单位分 别是cmg和cm3mo。磁感应强度S1单位是特[斯拉](T),而过去习惯使用的单位是 高斯G,1T=10'G 2.分子磁矩与磁化率 物质的磁性与组成它的原子、离子或分子的微观结构有关,在反磁性物质中,由于电子 自旋已配对,故无永久磁矩。但是内部电子的轨道运动,在外磁场作用下产生的拉摩进动, 会感生出一个与外磁场方向相反的诱导磁矩,所以表示出反磁性。其侧就等于反磁化率X反 所以具有永久磁矩。在外磁场中,永久 ,产生顺磁性。顺磁性物质的摩尔磁化率XM是摩尔顺破化率与磨 尔反磁化率之和,即 yM=y+y历 (51 通常X展比X大约1~3个数量级,所以这类物质总表现出顺磁性,其>0。顺磁化率与 分子永久磁矩的关系服从居里定律 - 3KT ⊙ 式中,Na为Avogadro常数:K为Boltzmann常数(1.38x1016ergK;T为热力学温度:m为分子 永久磁矩(ergG)。由此可得 + 今
第二部分,结构化学实验 实验一 磁化率的测定 一、实验目的 1.掌握古埃(Gouy)法测定磁化率的原理和方法。 2.测定三种络合物的磁化率,求算未成对电子数,判断其配键类型。 3.了解磁天平的原理与测定方法。 二、基本原理 1.磁化率 : 物质在外磁场中,会被磁化并感生一附加磁场,其磁场强度 H′与外磁场强 度 H 之和称为该物质的磁感应强度 B,即 B = H + H′ (1) H′与 H 方向相同的叫顺磁性物质,相反的叫反磁性物质。还有一类物质如铁、钴、镍及其 合金,H′比 H 大得多(H′/H)高达 104,而且附加磁场在外磁场消失后并不立即消失,这 类物质称为铁磁性物质。 物质的磁化可用磁化强度 I 来描述,H′=4πI。对于非铁磁性物质, I 与外磁场强度 H 成正比 I = KH (2) 式中,K 为物质的单位体积磁化率(简称磁化率),是物质的一种宏观磁性质。在化学中常用 单位质量磁化率 χm 或摩尔磁化率 χM表示物质的磁性质,它的定义是 χm = K/ρ (3) χM = MK/ρ (4) 式中,ρ 和 M 分别是物质的密度和摩尔质量。由于 K 是无量纲的量,所以 χm 和 χM的单位分 别是 cm 3 ·g -1 和 cm 3 ·mol-1。 磁感应强度 SI 单位是特[斯拉](T),而过去习惯使用的单位是 高斯(G),1T=104 G。 2.分子磁矩与磁化率 物质的磁性与组成它的原子、离子或分子的微观结构有关,在反磁性物质中,由于电子 自旋已配对,故无永久磁矩。但是内部电子的轨道运动,在外磁场作用下产生的拉摩进动, 会感生出一个与外磁场方向相反的诱导磁矩,所以表示出反磁性。其 χM就等于反磁化率 χ 反, 且 χM<0。在顺磁性物质中,存在自旋未配对电子,所以具有永久磁矩。在外磁场中,永久 磁矩顺着外磁场方向排列,产生顺磁性。顺磁性物质的摩尔磁化率 χM 是摩尔顺磁化率与摩 尔反磁化率之和,即 χM =χ 顺 + χ 反 (5) 通常 χ 顺比 χ 反大约1~3个数量级,所以这类物质总表现出顺磁性,其 χM>0。顺磁化率与 分子永久磁矩的关系服从居里定律 (6) 式中,NA 为 Avogadro 常数;K 为 Boltzmann 常数(1.38×10-16erg·K-1 );T 为热力学温度;μm为分子 永久磁矩(erg·G-1 )。由此可得 (7)

由于X不随温度变化(或变化极小),所以只要测定不同温度下的M对1T作图,截矩即为x ,由斜率可求。由于比X小得多,所以在不很精确的测量中可忽略X作近似处理 Yw=Y= ,(cm3,mol-) 3KT 顺磁性物质的4m与未成对电子数n的关系为 4,=48V8+② (9) 式中,以是玻尔磁子,其物理意义是:单个自由电子自旋所产生的磁矩 4g-9.273×104ergG2=9.273×102-G2=9.273×24-T1 3.磁化率与分子结构 (6)式将物质的宏观性质y,与微观性质山。联系起来。由实验测定物质的,根据(8)式 可求得 进而计算未配对电子数。这些结果可用于研究原子或离子的电子结构,判断 络合物分子的配健类型 络合物分为电价络合物和共价络合物。电价络合物中心离子的电子结构不受配位体的是 响,基本上保持自由离子的电子结构,靠静电库仑力与配位体结合,形成电价配键。在这类 络合物中,含有较多的自旋平行电子,所以是高自旋配位化合物。共价络合物则以中心离子 空的价电子轨道接受配位体的孤对电子,形成共价配键,这类络合物形成时,往往发生申子 重挂,自旋平行的电子相对减少, 所以是低自旋配位化合物。例如C0”其外层电子结构为 在络离子(coF中,形成电价配键,电子排布为: D①①D○○O (a) 3d 4p 此时,未配对电子数n=4, ,=4.9ug。C0以上面的结构与6个F.以静电力相吸引形成电价 DDD○OOO○ 此时.0, 。=0。Co"将6个电子集中在3个3d轨道上,6个CN的孤对电子进入Co"的 六个空轨道d杂化轨道,形成其价合物 4.古埃法测定磁化率 古埃磁天平如图1所示。天平左臂悬挂一样品管,管底部处于磁场强度最大的区域(), 管顶端则位于场强最弱(甚至为零)的区域(H)。整个样品管处于不均匀磁场中。设圆柱形样 品的截面积为A,沿样品管长度方向上d血长度的体积A在非均匀磁场中受到的作用力dF dF=KAH de 式中,K为体积磁化率H为磁场强度:dH/z为场强梯度, 积分上式得 F=-(K-KHHA (11) 式中,K。为样品周围介质的体积磁化率(通常是空气, 图1古挨磁天平工作原理示意图
由于 χ 反不随温度变化(或变化极小),所以只要测定不同温度下的 χM对 1/T 作图,截矩即为 χ 反,由斜率可求 μm。由于比 χ 顺小得多,所以在不很精确的测量中可忽略 χ 反作近似处理 (8) 顺磁性物质的 μm 与未成对电子数 n 的关系为 (9) 式中,μB 是玻尔磁子,其物理意义是:单个自由电子自旋所产生的磁矩。 μB=9.273×10-21erg·G-1 =9.273×10-28J·G-1 =9.273×-24J·T-1 3.磁化率与分子结构 (6)式将物质的宏观性质 χM与微观性质 μm 联系起来。由实验测定物质的 χM,根据(8)式 可求得 μm,进而计算未配对电子数 n。这些结果可用于研究原子或离子的电子结构,判断 络合物分子的配键类型。 络合物分为电价络合物和共价络合物。电价络合物中心离子的电子结构不受配位体的影 响,基本上保持自由离子的电子结构,靠静电库仑力与配位体结合,形成电价配键。在这类 络合物中,含有较多的自旋平行电子,所以是高自旋配位化合物。共价络合物则以中心离子 空的价电子轨道接受配位体的孤对电子,形成共价配键,这类络合物形成时,往往发生电子 重排,自旋平行的电子相对减少,所以是低自旋配位化合物。例如 Co3+其外层电子结构为 3d6,在络离子(CoF6) 3-中,形成电价配键,电子排布为: 3d 4s 4p (a) 此时,未配对电子数 n=4,μm =4.9μB。Co3+以上面的结构与 6 个 F-以静电力相吸引形成电价 络合物。而在[Co(CN)6]3- 中则形成共价配键,其电子排布为: 3d 4s 4p (b) 此时,n=0,μ m =0。Co3+将 6 个电子集中在 3 个 3d 轨道上,6 个 CN-的孤对电子进入 Co3+的 六个空轨道(d 2 sp 3杂化轨道),形成共价络合物。 4.古埃法测定磁化率 古埃磁天平如图 1 所示。天平左臂悬挂一样品管,管底部处于磁场强度最大的区域(H), 管顶端则位于场强最弱(甚至为零)的区域(H0)。整个样品管处于不均匀磁场中。设圆柱形样 品的截面积为 A,沿样品管长度方向上 dz 长度的体积 Adz 在非均匀磁场中受到的作用力 dF 为 (10) 式中,K 为体积磁化率;H 为磁场强度;dH/dz 为场强梯度, 积分上式得 (11) 式中,K0为样品周围介质的体积磁化率(通常是空气, 图 1 古挨磁天平工作原理示意图

K。值很小)。 如果K可以忽略,且Ho=0时,整个样品受到的力为 F=-KHA (12) 在非均匀磁场中,顺磁性物质受力向下所以增重:而反磁性物质 受力向上所以减重。测定时在天平右臂加减砝码使之平衡。设△W为施加磁场前后的称量 差,则 F=-KH2A=gAW (13) p-入上试湖 由于K=XP w-2用awge4emg (14) WH2 式中,△W空管,特品为样品管加样品后在施加磁场前后的称量差(g△W空等为空样品管在施加磁 场前后的称量差g;g为重力加速度980cms:h为样品高度(cm:M为样品的摩尔质量 (e-mor);w为样品的质量gH为磁极中心磁场强度G。 在精确的测量中,通常用莫尔氏盐来标定磁场强度,它的单位质量磁化率与热力学温度 (T)的关系为T=273+t 么-10a29 (15) 三、仪器药品 古埃磁天平(包括电磁铁, FD-F-A磁天平 电光天平,励磁电源, 特斯拉计)软质玻璃样品管 产口式剂新 英尔氏盐NH,hs0 +FeSO6H,0 (分析纯)FeS07H,0(分析纯) 电流调节校正 宰 K,Fe(CN63HzO(分析纯) 电可 小漏斗 四、实验步骤 图2毫特斯拉计面板图 1.记录实验室温度 1.磁极中心磁场强度的测定 (1)将霍尔变送器探头平面垂直放入磁极中心处,通电源,预热5分钟以后,调节“电流 调节”、“调零”电位器使“A”和“T”表显示为零。调节电流电位器使A表显示为10.00 观察mT表的值应在850士50,有误差可再检查探头间距或方向:如果误差较大,则用螺丝 刀转动校正电位器使数值达到要求 (2)用莫尔氏盐标定①取一干洁的空样品管悬挂在磁天平左臂挂钩上,样品管应与磁极中 心线平齐,注意样品管不要与磁极相触。准确称取空管的质量W空(H0),接通励磁电源调 节电流,使H=150mT(1mT=10G),称取空管的质量W空(H=150mT)。将隧场提高300mT后
K0值很小)。 如果 K0可以忽略,且 H0=0 时,整个样品受到的力为 (12) 在非均匀磁场中,顺磁性物质受力向下所以增重;而反磁性物质 受力向上所以减重。测定时在天平右臂加减砝码使之平衡。设Δ W 为施加磁场前后的称量 差,则 (13) 由于 代入上式得 (14) 式中,Δ W 空管+样品为样品管加样品后在施加磁场前后的称量差(g);ΔW 空管为空样品管在施加磁 场前后的称量差(g); g 为重力加速度(980cm·s -2 ); h 为样品高度(cm); M 为样品的摩尔质量 (g·mol-1 ); W 为样品的质量(g); H 为磁极中心磁场强度(G)。 在精确的测量中,通常用莫尔氏盐来标定磁场强度,它的单位质量磁化率与热力学温度 (T)的关系为 T=273+t (15) 三、仪器药品 古埃磁天平(包括电磁铁, 电光天平,励磁电源, 特斯拉计) 软质玻璃样品管 广口试剂瓶 莫尔氏盐(NH4)2SO4·FeSO4·6H2O (分析纯) FeSO4·7H2O(分析纯) K4Fe(CN)6·3H2O(分析纯) 小漏斗 四、实验步骤 1.记录实验室温度; 1.磁极中心磁场强度的测定 (1)将霍尔变送器探头平面垂直放入磁极中心处,通电源,预热 5 分钟以后,调节“电流 调节”、“调零”电位器使“A”和“mT”表显示为零。调节电流电位器使 A 表显示为 10.00。 观察 mT 表的值应在 850±50,有误差可再检查探头间距或方向;如果误差较大,则用螺丝 刀转动校正电位器使数值达到要求。 (2)用莫尔氏盐标定 ①取一干洁的空样品管悬挂在磁天平左臂挂钩上,样品管应与磁极中 心线平齐,注意样品管不要与磁极相触。准确称取空管的质量 W 空管(H=0),接通励磁电源调 节电流,使 H=150mT(1mT =10 G),称取空管的质量 W 空管(H=150mT)。将磁场提高 300mT 后 图 2 毫特斯拉计面板图
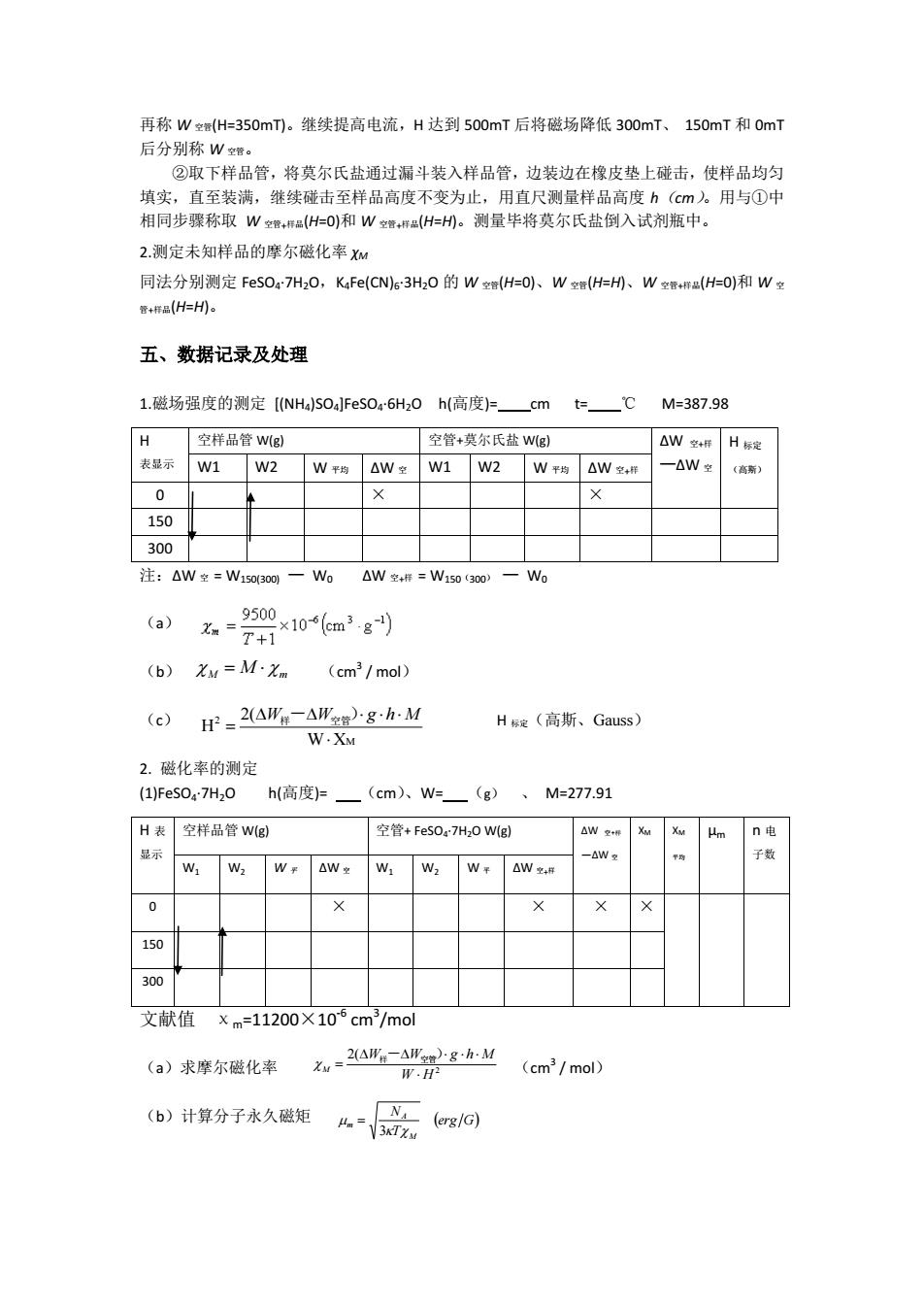
再称W空H=350mT)。继续提高电流,H达到500mT后将磁场降低300mT、150mT和0mT 后分别称W和管 ②取下样品管,将莫尔氏盐通过漏斗装入样品管,边装边在橡皮垫上碰击,使样品均匀 填实,直至装满,继续碰击至样品高度不变为止,用直尺测量样品高度h(cm人用与中 相同步骤称取W普,H=0)和W:(H=州。测量毕将莫尔氏盐倒入试剂瓶中。 2.测定未知样品的摩尔磁化率x 同法分别测定FeSO4-7H2O,KFe(CNs3HO的W室H=O、W室(H=M、W(H=O)和W 五、数据记录及处理 1.磁场强度的测定【NHS0]FeS0a·6H0h(高度)=—cmt=一CM-387.98 H 空样品管Wg) 空管+莫尔氏盐Wg) △W释H标 表显示W1W2W均△W室W1W2W均△Wg# 一△W空 0 150 300 注:△W空=W1so30一W0△W室#=W1s030o Wa (a) 7×106m3g 9500 (b)Xw=M·n (cm3 mol) (c)H2(AWAWsghM H标R(高斯、Gauss) 2.磁化率的测定 (1)FeSO.7H2O h(高度) (cm)、w=(g) 、M=277.91 H表 空样品管w@ 空管+Fes0r7Hz0wgl △W+Xu Xw Hm n电 显示 子数 W:Wa ww2w△w X + 300 文献值 Xm=11200×10cm/mol (a)求摩尔磁化率 Zw2aw-8:4(em2/mod b)》计算分子永久矩么泛o
再称 W 空管(H=350mT)。继续提高电流,H 达到 500mT 后将磁场降低 300mT、 150mT 和 0mT 后分别称 W 空管。 ②取下样品管,将莫尔氏盐通过漏斗装入样品管,边装边在橡皮垫上碰击,使样品均匀 填实,直至装满,继续碰击至样品高度不变为止,用直尺测量样品高度 h(cm)。用与①中 相同步骤称取 W 空管+样品(H=0)和 W 空管+样品(H=H)。测量毕将莫尔氏盐倒入试剂瓶中。 2.测定未知样品的摩尔磁化率 χM 同法分别测定 FeSO4·7H2O,K4Fe(CN)6·3H2O 的 W 空管(H=0)、W 空管(H=H)、W 空管+样品(H=0)和 W 空 管+样品(H=H)。 五、数据记录及处理 1.磁场强度的测定 [(NH4)SO4]FeSO4·6H2O h(高度)= cm t= ℃ M=387.98 注:∆W 空 = W150(300) — W0 ∆W 空+样 = W150(300) — W0 (a) (b) (cm 3 / mol) (c) H 标定(高斯、Gauss) 2. 磁化率的测定 (1)FeSO4·7H2O h(高度)= (cm)、W= (g) 、 M=277.91 文献值 χm=11200×10-6 cm3 /mol (a)求摩尔磁化率 (cm 3 / mol) (b)计算分子永久磁矩 H 表显示 空样品管 W(g) 空管+莫尔氏盐 W(g) ∆W 空+样 —∆W 空 H 标定 W1 W2 W 平均 ∆W 空 W1 W2 W 平均 ∆W 空+样 (高斯) 0 × × 150 300 H 表 显示 空样品管 W(g) 空管+ FeSO4·7H2O W(g) ∆W 空+样 —∆W 空 XM XM 平均 μm n 电 子数 W1 W2 W 平 ∆W 空 W1 W2 W 平 ∆W 空+样 0 × × × × 150 300 M 2 W X 2( H W样- W空管)g h M M M m 2 2( W H W W g h M M 样- 空管) erg G T N M A m 3
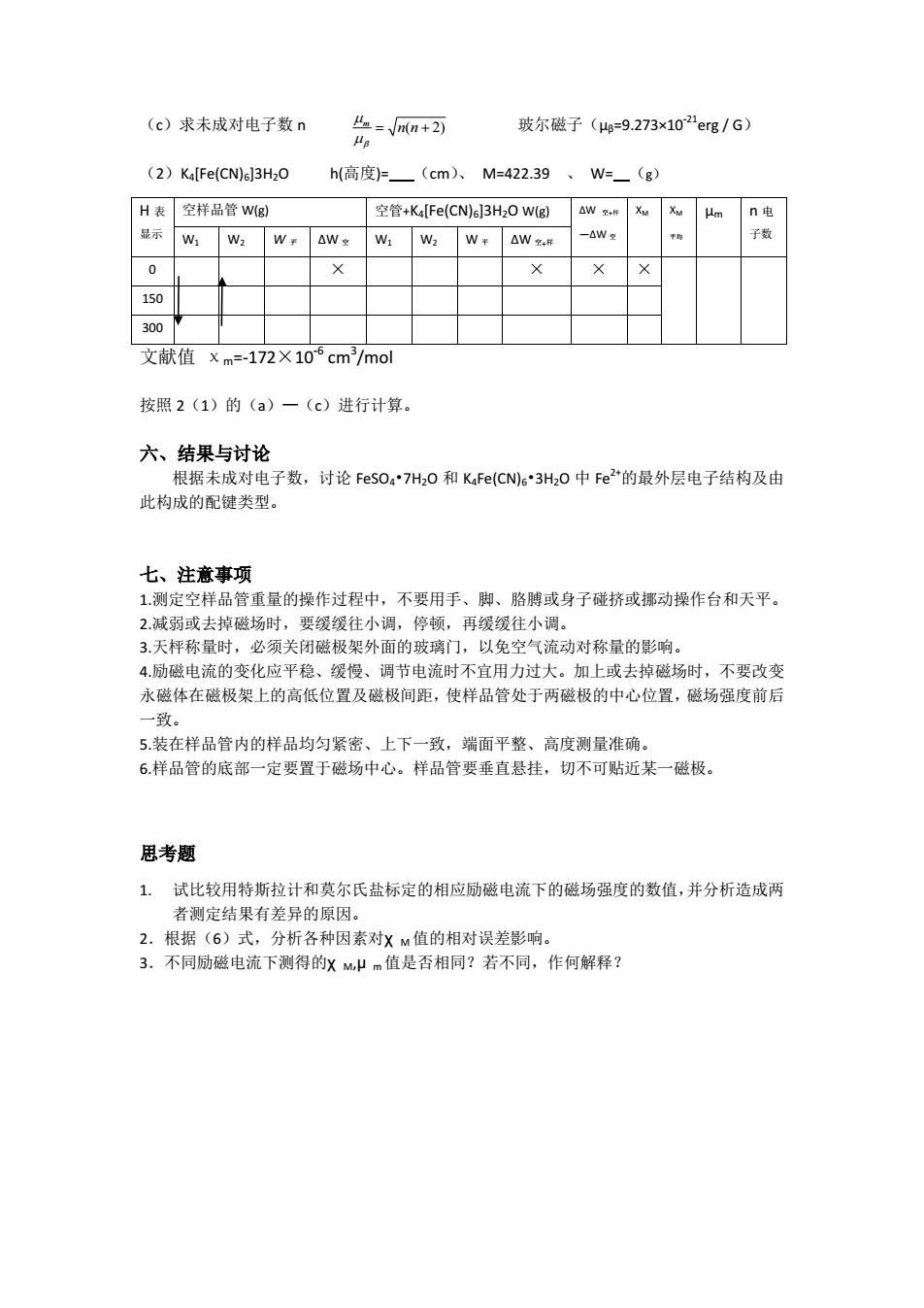
(c)求未成对电子数n 4=mn+2习 玻尔磁子(=9.273x102erg/G) (2)Ka[Fe(CN)e]3H2O h(高度F(cm、M-42239、W=(g) H表 空样品管wgl 空管+K4Fe(CN)63 H2O W(g)AW 2.m Xw X Lm n电 显示 150 300 文献值xm=-172X105cm/mol 按照2(1)的(a)一(c)进行计算。 六、结果与讨论 根据未成对电子数,讨论FeSO47H,0和KFe(CN)63H,0中Fe2“的最外层电子结构及由 此构成的配键类型。 七、注意事项 1测定空样品管重量的操作过程中,不要用手、脚、骼膊或身子碰挤或挪动操作台和天平。 2减弱或去掉磁场时,要缓缓往小调,停顷,再缓缓往小调。 3.天枰称量时,必须关闭磁极架外面的玻璃门,以免空气流动对称量的影响。 4.励磁电流的变化应平稳、 、调节电流时不宜用力过大。加上或去掉磁场时,不要改变 水磁体在磁极架上的高低位置及磁极间距,使样品管处于两磁极的中心位置,磁场强度前后 “致。 5装在样品管内的样品均匀紧密、上下一致,端面平整、高度测量准确。 6样品管的底部一定要置于磁场中心。样品管要垂直悬挂,切不可贴近某一磁极。 思考题 1.试比较用特斯拉计和莫尔氏盐标定的相应励磁电流下的磁场强度的数值,并分析造成两 者则定结果右差异的原因 2.根据(6)式,分析各种因素对XM值的相对误差影响 3.不同励磁电流下测得的xm值是否相同?若不同,作何解释
(c)求未成对电子数 n 玻尔磁子(μβ=9.273×10-21erg / G) (2)K4[Fe(CN)6]3H2O h(高度)= (cm)、 M=422.39 、 W= (g) 文献值 χm=-172×10-6 cm3 /mol 按照 2(1)的(a)—(c)进行计算。 六、结果与讨论 根据未成对电子数,讨论 FeSO4•7H2O 和 K4Fe(CN)6•3H2O 中 Fe2+的最外层电子结构及由 此构成的配键类型。 七、注意事项 1.测定空样品管重量的操作过程中,不要用手、脚、胳膊或身子碰挤或挪动操作台和天平。 2.减弱或去掉磁场时,要缓缓往小调,停顿,再缓缓往小调。 3.天枰称量时,必须关闭磁极架外面的玻璃门,以免空气流动对称量的影响。 4.励磁电流的变化应平稳、缓慢、调节电流时不宜用力过大。加上或去掉磁场时,不要改变 永磁体在磁极架上的高低位置及磁极间距,使样品管处于两磁极的中心位置,磁场强度前后 一致。 5.装在样品管内的样品均匀紧密、上下一致,端面平整、高度测量准确。 6.样品管的底部一定要置于磁场中心。样品管要垂直悬挂,切不可贴近某一磁极。 思考题 1. 试比较用特斯拉计和莫尔氏盐标定的相应励磁电流下的磁场强度的数值,并分析造成两 者测定结果有差异的原因。 2.根据(6)式,分析各种因素对χ M值的相对误差影响。 3.不同励磁电流下测得的χ M,μ m值是否相同?若不同,作何解释? H 表 显示 空样品管 W(g) 空管+K4[Fe(CN)6]3H2O W(g) ∆W 空+样 —∆W 空 XM XM 平均 μm n 电 W 子数 1 W2 W 平 ∆W 空 W1 W2 W 平 ∆W 空+样 0 × × × × 150 300 n(n 2) m