
第三章刚体的转动 出发点:牛顿质点运动定律 刚体的运动分为:平动,定轴转动,定点转动,平面平行运动,一般运 动。 §3-1刚体的平动,转动和定轴转动 一刚体的定义:在无论多大力作用下物体形状和大小均保持不变。(理想模 型) 二平动:在运动过程中,若刚体上任意一条直线在各个时刻的位置始终彼此 平行,则这种运动叫做平动。 特征:1平动时刚体中各质点的位移,速度,加速度相等。 2动力学特征:将刚体看成是一个各质点间距离保持不变的质点组。 受力:内力方和外力下 对每一个质元:满足牛顿运动定律F+方=Mia】 对刚体而言:∑(F+方上∑Miai →∑f+∑fi=∑Miai 显然∑i=0→∑F万=∑Mia=a∑M 故:∑F=Ma 即:刚体做平动时,其运动规律和一质点相当,该质点的质量与刚体的质量 相等,所受的力等于刚体所受外力的矢量和。 三转动和定轴转动 定轴转动的运动学特征:用角位移、角速度、角加速度加以描述,且刚体中 各质点的角位移、角速度、角加速度相等
第三章 刚体的转动 出发点:牛顿质点运动定律 刚体的运动分为:平动,定轴转动,定点转动,平面平行运动,一般运 动。 §3-1 刚体的平动,转动和定轴转动 一 刚体的定义:在无论多大力作用下物体形状和大小均保持不变。(理想模 型) 二 平动:在运动过程中,若刚体上任意一条直线在各个时刻的位置始终彼此 平行,则这种运动叫做平动。 特征:1 平动时刚体中各质点的位移,速度,加速度相等。 2 动力学特征:将刚体看成是一个各质点间距离保持不变的质点组。 受力:内力 fi 和外力 Fi 对每一个质元:满足牛顿运动定律 Fi + fi =Mi a i 对刚体而言: ( Fi + fi )= Mi a i Fi + fi = Mi a i 显然 fi =0 Fi = Mi a I=a Mi 故: F ==M a 即:刚体做平动时,其运动规律和一质点相当,该质点的质量与刚体的质量 相等,所受的力等于刚体所受外力的矢量和。 三 转动和定轴转动 定轴转动的运动学特征:用角位移、角速度、角加速度加以描述,且刚体中 各质点的角位移 、角速度、角加速度相等。 = dt d , = dt d

对匀速、匀变速转动可参阅P210表4-2 角量与线量的关系: V=Ro at=Ra an=0R 转轴 转动平面 参考方向一 更一般的形式:角速度矢量的定义: i-ax7,a-da 显然,定轴转动的运动学问题与质点的圆周运动相同。 例:一飞轮在时间t内转过角度0=al+bf-cf,式中abc都是常量。求它的角加 速度。 解:飞轮上某点的角位置可用0表示为0=at+b1ct,将此式对t求导数, 即得飞轮角速度的表达式为 o=a+bie=动f1 角加速度是角速度对t导数,因此得 a会ed 由此可见,飞轮作的是变加速转动 §3-2力距刚体定轴转动定律 一力矩:设F在转动平面内
对匀速、匀变速转动可参阅 P210 表 4-2 角量与线量的关系: v=R at=R an= 2 R 转轴 转动平面 o 参考方向 更一般的形式:角速度矢量的定义: = , = dt d 显然,定轴转动的运动学问题与质点的圆周运动相同。 例:一飞轮在时间 t 内转过角度 = t at b 3 + -c t 4 ,式中 abc 都是常量。求它的角加 速度。 解: 飞轮上某点的角位置可用 表示为 = t at b 3 + -c t 4 ,将此式对 t 求导数, 即得飞轮角速度的表达式为 = ( dt d t at b 3 + -c t 4 )=a+3b t 2 -4c t 3 角加速度是角速度对 t 导数,因此得 = dt d = dt d ( a+3b t 2 -4c t 3 )=6bt-12c t 2 由此可见,飞轮作的是变加速转动。 §3-2 力距 刚体定轴转动定律 一 力矩:设 F 在转动平面内
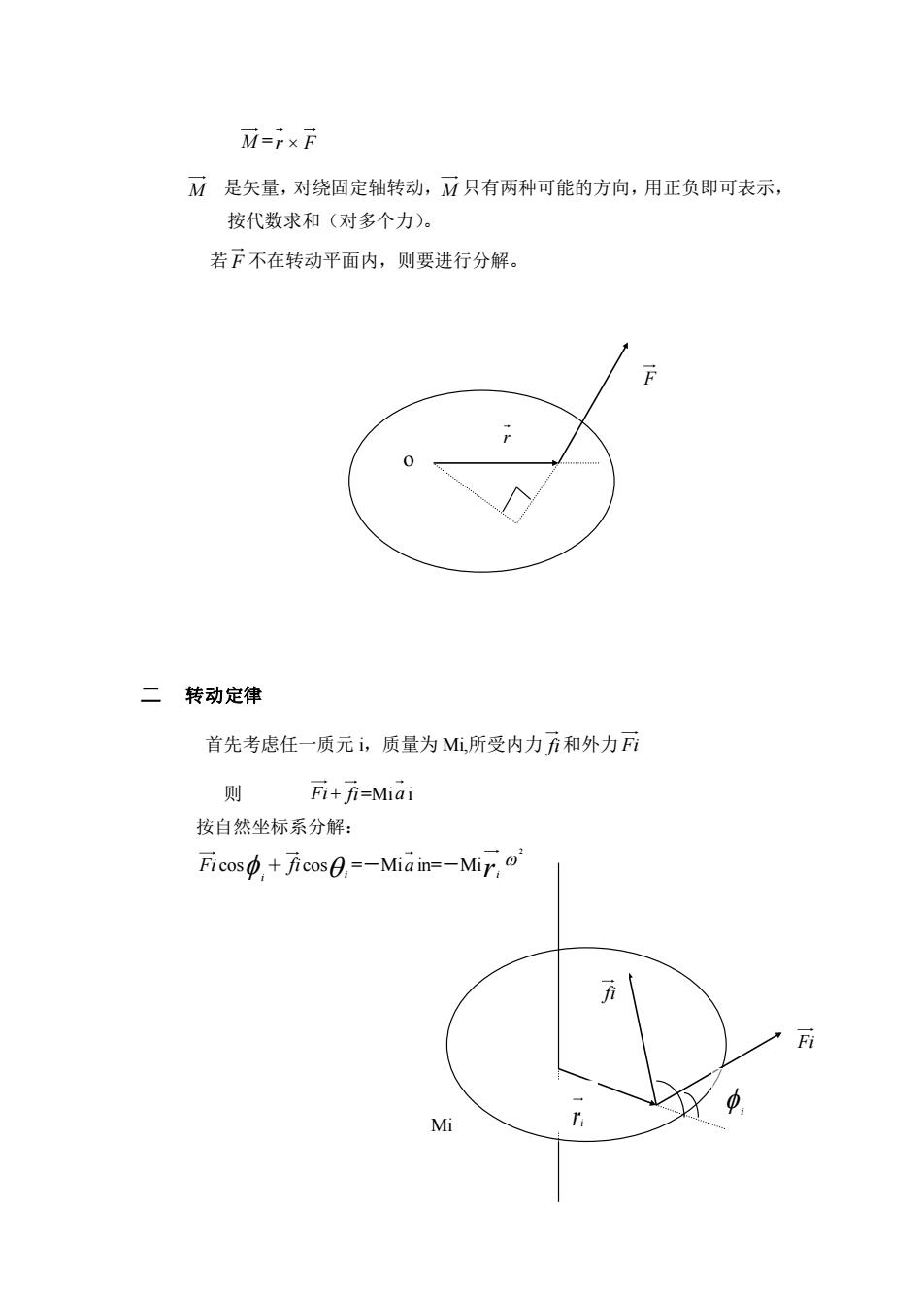
M=×F 应是矢量,对绕固定轴转动,M只有两种可能的方向,用正负即可表示, 按代数求和(对多个力)。 若F不在转动平面内,则要进行分解 二转动定律 首先考虑任一质元i,质量为M,所受内力方和外力 则 Fi+fi=Mia 按自然坐标系分解: Ficos+ficos,=-Miain-Mir, M
M = r F M 是矢量,对绕固定轴转动, M 只有两种可能的方向,用正负即可表示, 按代数求和(对多个力)。 若 F 不在转动平面内,则要进行分解。 二 转动定律 首先考虑任一质元 i,质量为 Mi,所受内力 fi 和外力 Fi 则 Fi + fi =Mi a i 按自然坐标系分解: Fi cos i + fi cos i =-Mi a in=-Mi ri 2 i r F o Fi Mi ri fi i

Fisin+fisin=Miait=Mir,a 第二式×r,得 F元snp,+元元,sm日=Mr,'a 对整个刚体 ∑Fir,simp,+∑ir,sim8,=∑(Mir)a :∑方r,sm0,=0. .内力距相互抵消 →∑ir,sm中-∑(Miri)a 令小∑(M,).称为刚体的转动惯量 而M.=∑ir,s血中 .总(合)外力距 M=a-9 故 .刚体的转动定律 (与牛顿第二定律比较) 三转动惯量的计算 1质点组 J∑(Mr) 川rpdv体令市 川r面令市 2质量连续分布 ∫rdmn= rl线分有 J是物体在转动中惯性大小的量度,决定于刚体各部分质量对给定转轴 的分布情况。 例:求质量为m长1的均匀细棒对下面三种转轴的转动惯量: (1)转轴通过棒的中心并和棒垂直: (2)转轴通过棒的一端并和棒垂直: (3)转轴通过棒上距中心为h的一点并和棒垂直
Fi sin i + fi sin i =Mi a it=Mi ri 第二式× ri 得 Fi ri sin i + fi ri sin i =Mi ri 2 对整个刚体 Fi ri sin i + fi ri sin i = ( Mi ri 2 ) fi ri sin i =0.内力距相互抵消 Fi ri sin i = ( Mi ri 2 ) 令 J= ( Mi ri 2 ).称为刚体的转动惯量 而 M z = Fi ri sin i .总(合)外力距 故 M z =J = J dt d . 刚体的转动定律 (与牛顿第二定律比较) 三 转动惯量的计算 1 质点组 J= ( Mi ri 2 ) 2 质量连续分布 J= r dm2 ={ 线 分 布 面 分 布 体 分 布 dl ds d r r r 2 2 2 J 是物体在转动中惯性大小的量度,决定于刚体各部分质量对给定转轴 的分布情况。 例:求质量为 m 长 l 的均匀细棒对下面三种转轴的转动惯量: (1) 转轴通过棒的中心并和棒垂直; (2) 转轴通过棒的一端并和棒垂直; (3) 转轴通过棒上距中心为 h 的一点并和棒垂直
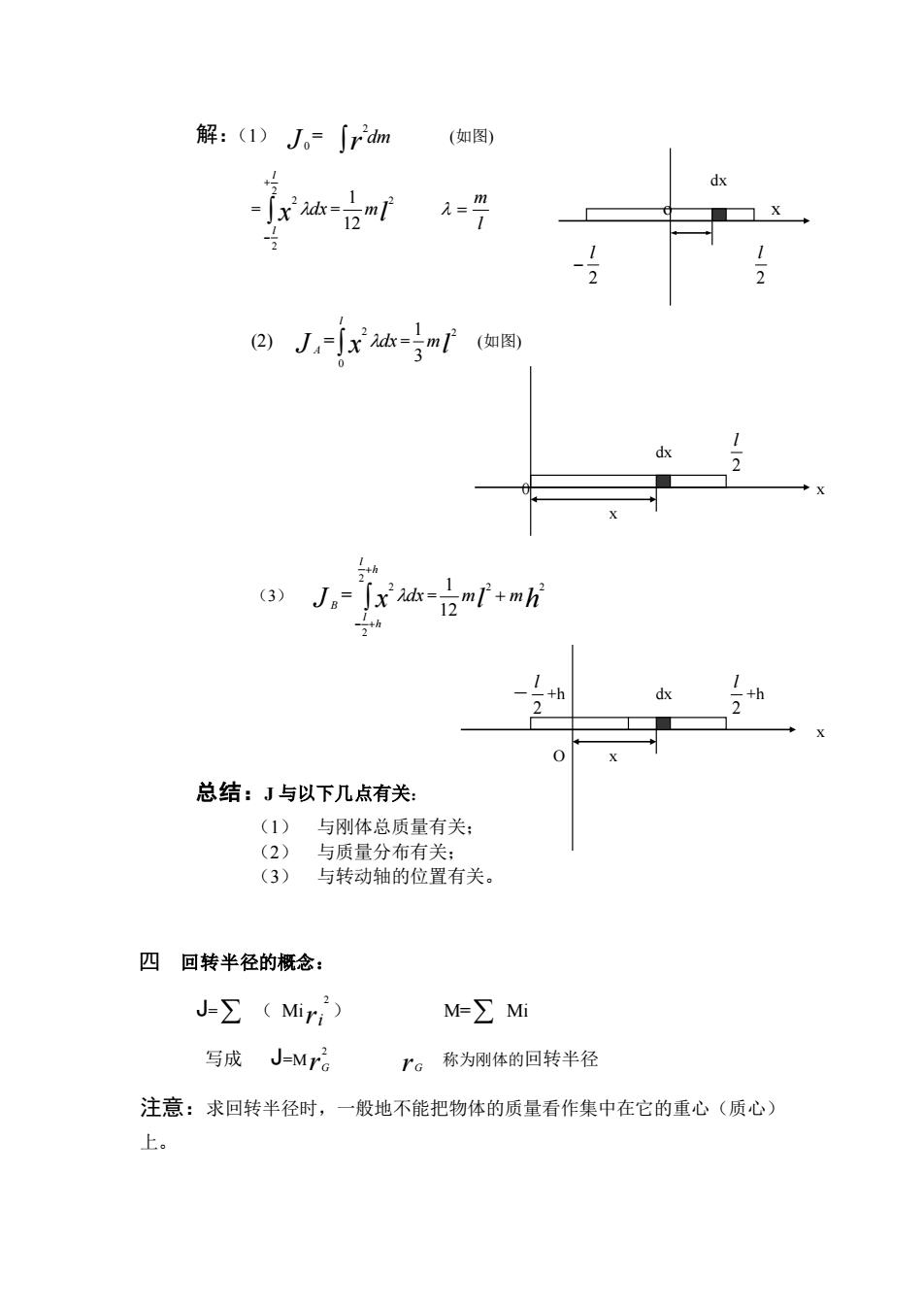
解:(1)J。=∫rm (如图) -了x迹=m=四 2)Jjx迹=m如图 (3)J。=∫x mf+m 总结:J与以下几点有关: (1)与刚体总质量有关: (2)与质量分布有关: (3)与转动轴的位置有关。 四回转半径的概念: J-∑(Mir;) M=∑Mi 写成J-Mra r。称为刚体的回转半径 注意:求回转半径时,一般地不能把物体的质量看作集中在它的重心(质心) 上
解:(1) J 0 = r dm2 (如图) = + − 2 2 2 l l x dx = ml 2 12 1 l m = o x (2) J A = l x dx 0 2 = ml 2 3 1 (如图) dx 2 l 0 x x (3) J B = + − + h l h l x dx 2 2 2 = ml mh 2 2 12 1 + - 2 l +h dx 2 l +h x O x 总结:J 与以下几点有关: (1) 与刚体总质量有关; (2) 与质量分布有关; (3) 与转动轴的位置有关。 四 回转半径的概念: J= ( Mi ri 2 ) M= Mi 写成 J=M r G 2 r G 称为刚体的回转半径 注意:求回转半径时,一般地不能把物体的质量看作集中在它的重心(质心) 上。 dx 2 l − 2 l