
2.2参数Bo、B的估计 一、普通最小二乘估计 (Ordinary Least Square Estimation,简记为OLSE) 最小二乘法就是寻找参数B。、B,的估计值使离差平方和达极小 Q(B。,月)=之(y-B。-Bx)尸 =min2oy-B。-Bx,)2 B,B )=B。+户,x,称为y的回归拟合值,简称回归值或拟合值 e,=y-少 称为y的残差
2 .2 参数β0、β1的估计 一、普通最小二乘估计 (Ordinary Least Square Estimation,简记为OLSE) n i i i n i i i y x Q y x 1 2 0 1 , 1 2 0 1 0 1 min ( ) ) ˆ ˆ ) ( ˆ , ˆ ( 0 1 最小二乘法就是寻找参数β0、β1的估计值使离差平方和达极小 i i y x 0 1 ˆ ˆ ˆ i i i e y y ˆ 称为yi的回归拟合值,简称回归值或拟合值 称为yi的残差
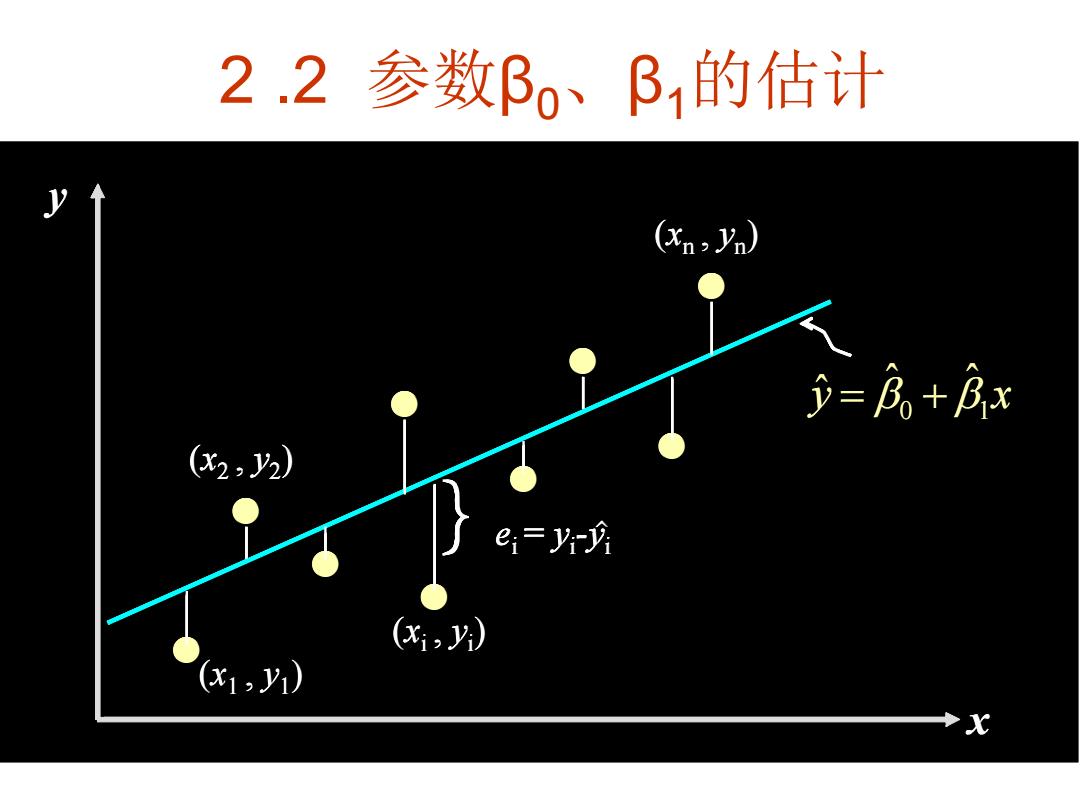
2.2参数B、B的估计 y (n>yn) ● =Bo+Bx (x2,2) ei=yi-y (x,y) (x1,y1)
2 .2 参数β0、β1的估计 x y (xn , yn ) (x1 , y1 ) (x 2 , y2 ) (xi , yi ) }ei = yi -y^i y x 0 1 ˆ ˆ yˆ x 0 1 ˆ ˆ ˆ x y (xn , yn ) (x1 , y1 ) (x 2 , y2 ) (xi , yi ) }ei = yi -y^i y x 0 1 ˆ ˆ yˆ x 0 1 ˆ ˆ ˆ x y (xn , yn ) (x1 , y1 ) (x 2 , y2 ) (xi , yi ) }ei = yi -y^i x y (xn , yn ) (x1 , y1 ) (x 2 , y2 ) (xi , yi ) }ei = yi -y^i (x 2 , y2 ) (xi , yi ) }ei = yi -y^i ei = yi -y^i y x 0 1 ˆ ˆ yˆ x 0 1 ˆ ˆ ˆ

2.2参数Bo、B1的估计 服R=A=-20-A-x)=0 8 含=0 A=A-22y-月-月x=0 80 经整理后,得正规方程组 哦+(区月=立y ②成+2a-2
2 .2 参数β0、β1的估计 ) 0 ˆ ˆ 2 ( ˆ ) 0 ˆ ˆ 2 ( ˆ 1 0 1 1 1 1 1 0 1 0 0 0 n i i i i n i i i y x x Q y x Q 经整理后,得正规方程组 n i n i n i i i i i n i i n i i x x x y n x y 1 1 1 1 2 0 1 1 1 0 ˆ ( ) ˆ ( ) ˆ ( ) ˆ 0 0 1 1 n i i i n i i x e e

2.2参数Bo、B1的估计 B。=少-月x 得OLSE为 2a-w西 26-列 人-立-2-m时 记 ,2-Wg-n-交-n时 B。=-Bx B.=Lg/La
2 .2 参数β0、β1的估计 2 1 1 1 0 1 ( ) ( )( ) ˆ ˆ ˆ n i i i n i i x x x x y y y x 得OLSE 为 n i n i xx i i L x x x n x 1 1 2 2 2 ( ) ( ) n i i i n i xy i i L x x y y x y nx y 1 1 ( )( ) Lxy Lxx y x / ˆ ˆ ˆ 1 0 1 记

2.2参数Bo、B的估计 续例2.1 x=492-328,D=3962=26415 15 15 Lo=x-) =196.16-15(3.28)2=34.784 L=∑y-nx万 =1470.65-1299.536=171.114 [B,=-Bx=26.413-4.919×3.28=10.279 B=L,/L=171.114/34.784=4.919 )=10.279+4.919x 回归方程
2 .2 参数β0、β1的估计 26.413 15 396.2 3.28 , 15 49.2 x y 196.16 15(3.28) 34.784 ( ) 2 1 2 2 n i xx i L x n x 1470.65 1299.536 171.114 1 n i xy i i L x y n x y / 171.114/ 34.784 4.919 ˆ 26.413 4.919 3.28 10.279 ˆ ˆ 1 0 1 Lxy Lxx y x y ˆ 10.279 4.919x 续例2.1 回归方程