
实验曲线 Mo(T)/W·cm2·um) 1700K 1500K 1300K 100 2 aum 3 5 绝对黑体的辐出度按波长分布曲线 6
6 1700K 1500K 1300K 1100K ( )/( ) 2 1 0 M T W cm m 0 1 2 3 4 5 / m 绝对黑体的辐出度按波长分布曲线 实验曲线

3.普朗克量子假设 问题:如何从理论上找到符合实验曲线的函数式 Mo(T)=f(九,T) 维恩经验公式 _C2 Mio(T)=C A-5e zi 这个公式与实验曲线波长短处符合得很好,但在波长 很长处与实验曲线相差较大。 7
7 问题:如何从理论上找到符合实验曲线的函数式 3. 普朗克量子假设 ( ) ( , ) M 0 T f T T C M T C e 2 5 0 1 ( ) 这个公式与实验曲线波长短处符合得很好,但在波长 很长处与实验曲线相差较大

瑞利-金斯经验公式 M0(T)=C324T 这个公式在波长很长处与实验曲线比较相近, 但在短波区,按此公式,M,。将随波长趋向于零而 趋向无穷大的荒谬结果,即“紫外灾难”。 维恩公式和瑞利金斯公式都是用经典物理学的 方法来研究热辐射所得的结果,都与实验结果不符, 明显地暴露了经典物理学的缺陷。黑体辐射实验是 物理学晴朗天空中一朵令人不安的乌云
8 M T C T 4 0 3 ( ) 这个公式在波长很长处与实验曲线比较相近, 但在短波区,按此公式, 将随波长趋向于零而 趋向无穷大的荒谬结果,即“紫外灾难” 。 M 0 维恩公式和瑞利-金斯公式都是用经典物理学的 方法来研究热辐射所得的结果,都与实验结果不符, 明显地暴露了经典物理学的缺陷。黑体辐射实验是 物理学晴朗天空中一朵令人不安的乌云

为了解决上述困难,普朗克利用内插法将适 用于短波的维恩公式和适用于长波的瑞利-金斯公 式衔接起来,提出了一个新的公式: M0=2πhc22 hc eikt -1 h=6.6260755×10-34J.s 普朗克常数 这一公式称为普朗克公式。它与实验结果符 合得很好
9 为了解决上述困难,普朗克利用内插法将适 用于短波的维恩公式和适用于长波的瑞利-金斯公 式衔接 起来,提出了一个新的公式: 1 1 2 2 5 0 kT hc e M hc h J s 34 6.6260755 10 普朗克常数 这一公式称为普朗克公式。它与实验结果符 合得很好
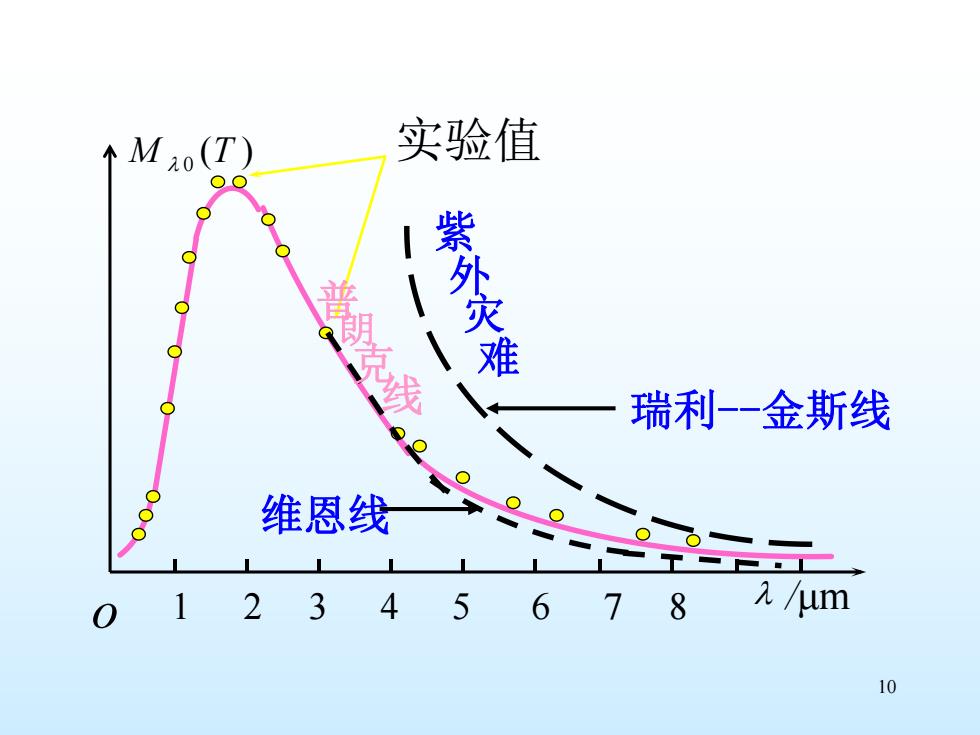
M2o(T) 实验值 配 游子举 瑞利-金斯线 维恩线 2345678 元/um 10
10 o 实验值 /μm ( ) M 0 T 维恩线 瑞利-金斯线 紫 外 灾 难 普朗克线 1 2 3 4 5 6 7 8