
优化一微积分方法 为了优化,首先要将目标函数进行表达,目标函数应表示成 独立变量的函数。 如果目标函数(如成本)能表示成: F=F(x1,X2,) 则最优解可通过对F进行微分,然后让导数为零得到。 f F =…=0 1 原则上,还须求出二阶导数以确定是否为最大或最小解。 6
6 为了优化,首先要将目标函数进行表达,目标函数应表示成 独立变量的函数。 如果目标函数(如成本)能表示成: 则最优解可通过对F进行微分,然后让导数为零得到。 原则上,还须求出二阶导数以确定是否为最大或最小解。 优化—微积分方法 F F x1 , x2 , F x1 F x2 0

优化 通常,目标函数会有一个或多个约束。 G(x2,)≤01=1,2.… H(1,x2,)=0i=1,2… 7
7 优化 通常,目标函数会有一个或多个约束。 Gi x1 , x2 , 0;i 1,2 Hi x1 , x2 , 0;i 1,2
例1一容器的设计 假设你要做一个封闭的罐子或者圆柱形容器,能够装载的容积 为V。容器的壁厚给定。 需要确定容器高度(h)和半径)的关系,使得制作该容器所使用 的材料最少。 8
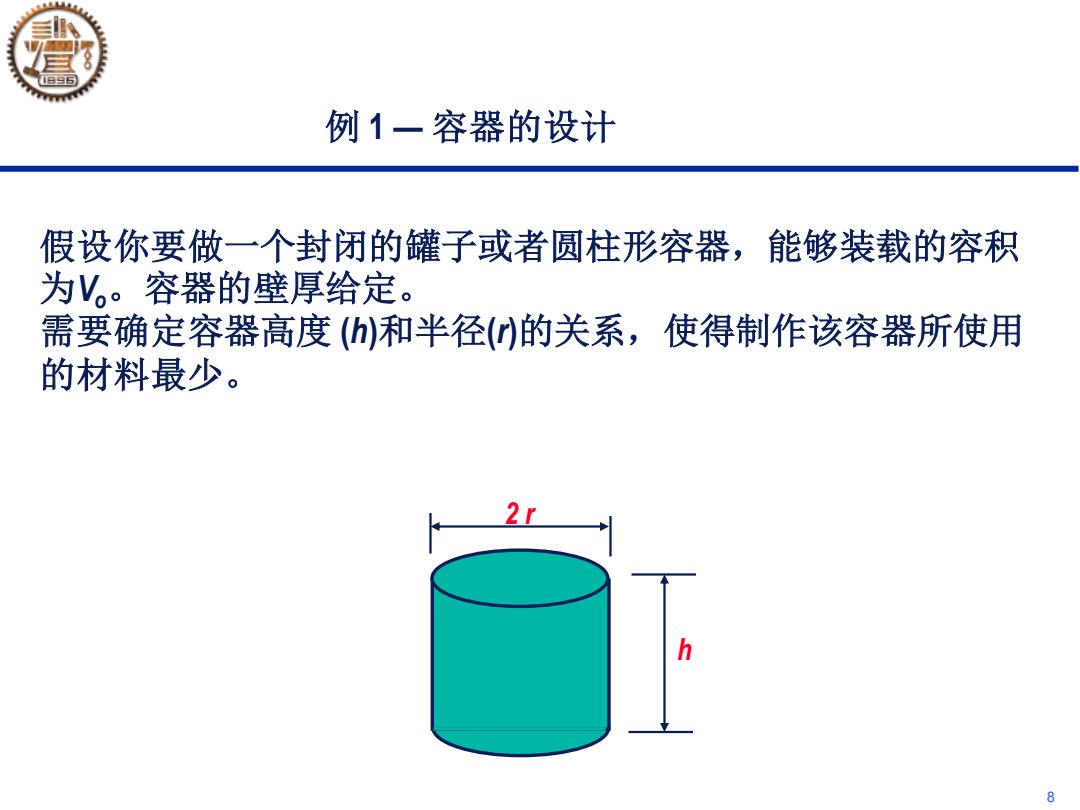
8 例 1 — 容器的设计 假设你要做一个封闭的罐子或者圆柱形容器,能够装载的容积 为Vo。容器的壁厚给定。 需要确定容器高度 (h)和半径(r)的关系,使得制作该容器所使用 的材料最少。 h 2 r

例1一容器的设计 假定该容器壁厚很小,相对于高度或半径可以忽略不计。 容器的容积为: %=π2h 表面积为: S=2πrh+2z2 消去高度参数,有: S=2亚+2m2 9
9 Vo r 2 h S 2 rh 2 r 2 假定该容器壁厚很小,相对于高度或半径可以忽略不计。 容器的容积为: 表面积为: 消去高度参数,有: S 2Vo r 2r 2 例 1 — 容器的设计

例1一容器的设计 对半径求导,并令其为零,有: ds dr 2y+4πr=0 or 2=3 4π 将容积公式带入,得: h=2r 或者说:直径与高度相等。 10
10 dS dr 2Vo r 2 4 r 0 2Vo 4 r 3 h 2r 对半径求导,并令其为零,有: or 将容积公式带入,得: 或者说:直径与高度相等。 例 1 — 容器的设计