
1、楔形薄膜的等厚条纹 分析 2入 3元/2 入 △x= 2/2 2sina 2a 2△x 正入射条件下 x相当于通过小的倾角α对进行了 干涉图样是平行于 放大,因此可以用于各种精密测量 交棱的直线
1、楔形薄膜的等厚条纹 分析 正入射条件下 2sin 2 x = 2 x Δx 相当于通过小的倾角 α 对 λ进行了 干涉图样是平行于 放大,因此可以用于各种精密测量 交棱的直线 x 2

应用测量:细丝、滚珠直径、表面光洁度、热涨系数 细丝 表面光洁度 滚珠 标准块规 标准石英环 待测工件 标准石英 热涨系数
应用 测量:细丝、滚珠直径、表面光洁度、热涨系数
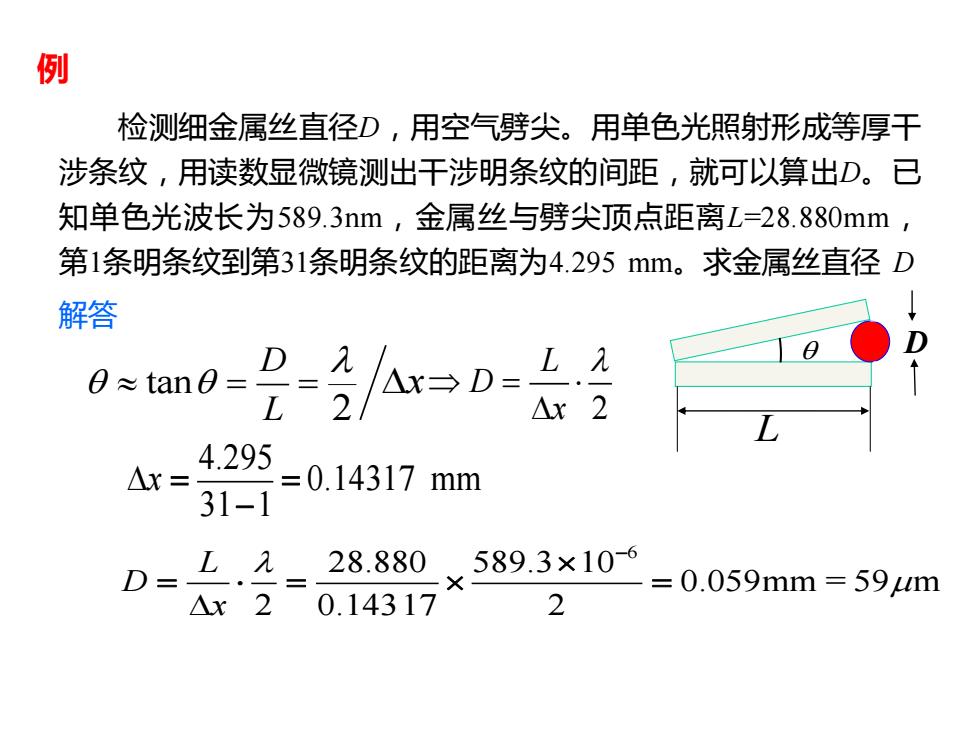
例 检测细金属丝直径D,用空气劈尖。用单色光照射形成等厚干 涉条纹,用读数显微镜测出干涉明条纹的间距,就可以算出D。已 知单色光波长为589.3nm,金属丝与劈尖顶点距离L=28.880mm, 第1条明条纹到第31条明条纹的距离为4.295mm。求金属丝直径D 解答 0≈tan0= D九 4.295 △x= =0.14317mm 31-1 D- L._28.880 △x20.14317 589.3×10=0.059mm=59m 2
例 检测细金属丝直径D,用空气劈尖。用单色光照射形成等厚干 涉条纹,用读数显微镜测出干涉明条纹的间距,就可以算出D。已 知单色光波长为589.3nm,金属丝与劈尖顶点距离L=28.880mm, 第1条明条纹到第31条明条纹的距离为4.295 mm。求金属丝直径 D D L tan 2 D L x = = 2 L D x = 4.295 0.14317 mm 31 1 x = = − 6 28.880 589.3 10 0.059mm = 59 m 2 0.14317 2 L D x − = = = 解答
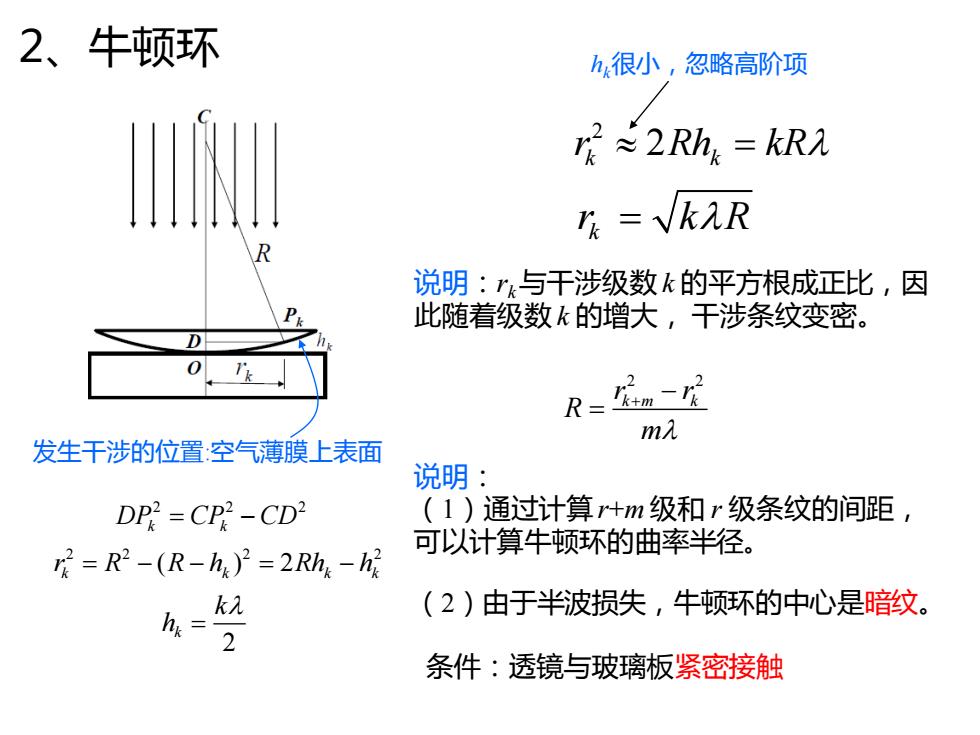
2、牛顿环 h很小,忽略高阶项 ≈2Rh=kR R=VkλR 说明:”与干涉级数k的平方根成正比,因 此随着级数k的增大,干涉条纹变密。 0 R= m入 发生干涉的位置空气薄膜上表面 说明: DP2=CP2-CD2 (1)通过计算+m级和r级条纹的间距, 可以计算牛顿环的曲率半径。 r=R2-(R-h)2=2Rhg-h2 k元 (2)由于半波损失,牛顿环的中心是暗纹。 hk= 2 条件:透镜与玻璃板紧密接触
2、牛顿环 2 2 2 DP CP CD k k = − 2 2 2 2 ( ) 2 k k k k r R R h Rh h = − − = − 2 k k h = 2 2 k k r Rh kR = kr k R = 说明:rk与干涉级数 k 的平方根成正比,因 此随着级数 k 的增大, 干涉条纹变密。 2 2 k m k r r R m + − = 说明: (1)通过计算r+m 级和 r 级条纹的间距, 可以计算牛顿环的曲率半径。 (2)由于半波损失,牛顿环的中心是暗纹。 条件:透镜与玻璃板紧密接触 hk很小,忽略高阶项 发生干涉的位置:空气薄膜上表面
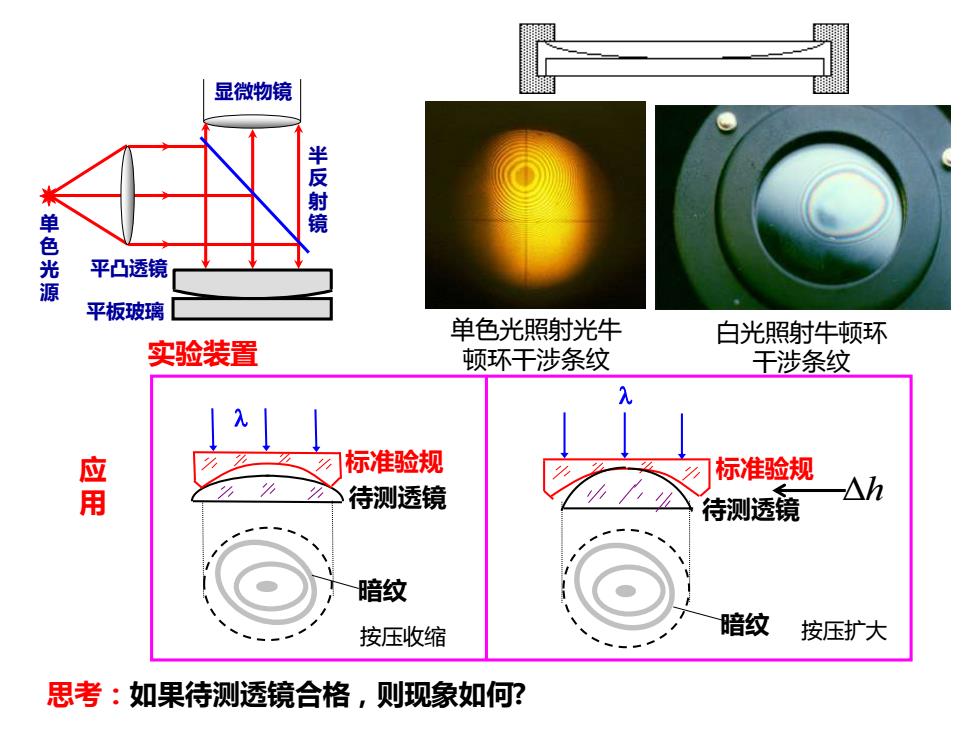
显微物镜 半反射镜 单 平凸透镜 源 平板玻璃 单色光照射光牛 白光照射牛顿环 实验装置 顿环干涉条纹 干涉条纹 应用 标准验规 标准验规 待测透镜 待测透镜 h 暗纹 按压收缩 暗纹 按压扩大 思考:如果待测透镜合格,则现象如何?
实验装置 单 色 光 源 显微物镜 平板玻璃 半 反 射 镜 平凸透镜 单色光照射光牛 顿环干涉条纹 白光照射牛顿环 干涉条纹 标准验规 待测透镜 暗纹 待测透镜 暗纹 标准验规 Δh 应 用 思考:如果待测透镜合格,则现象如何? 按压收缩 按压扩大