
电力线路的电压降落 2、i为流过复阻抗的电流,以相量U为参考轴, 如果i和cosp己知,可作出相量图如图3-2(b )所示。 02=01-(R+jX)i=U1-△U1+jU1 U=U2+(R+jx)I 立,AU1=RIcoso,+XIsing U RIsing +XIcoso U △U和U,分别称为电压 电压降落 降落的纵分量和横分量。 (b)
和 分别称为电压 降落的纵分量和横分量。 电力线路的电压降落 2、 为流过复阻抗的电流,以相量 为参考轴, 如果 和 已知,可作出相量图如图3-2(b )所示。 1 1 1 1 1 1 U RIsin XIcos U RIcos XIsin U U R jX)I 1 2 ( I I U1 I 1 cos 电压降落 U1 U1 2 1 1 1 U1 U U - R jX)I U -U j (
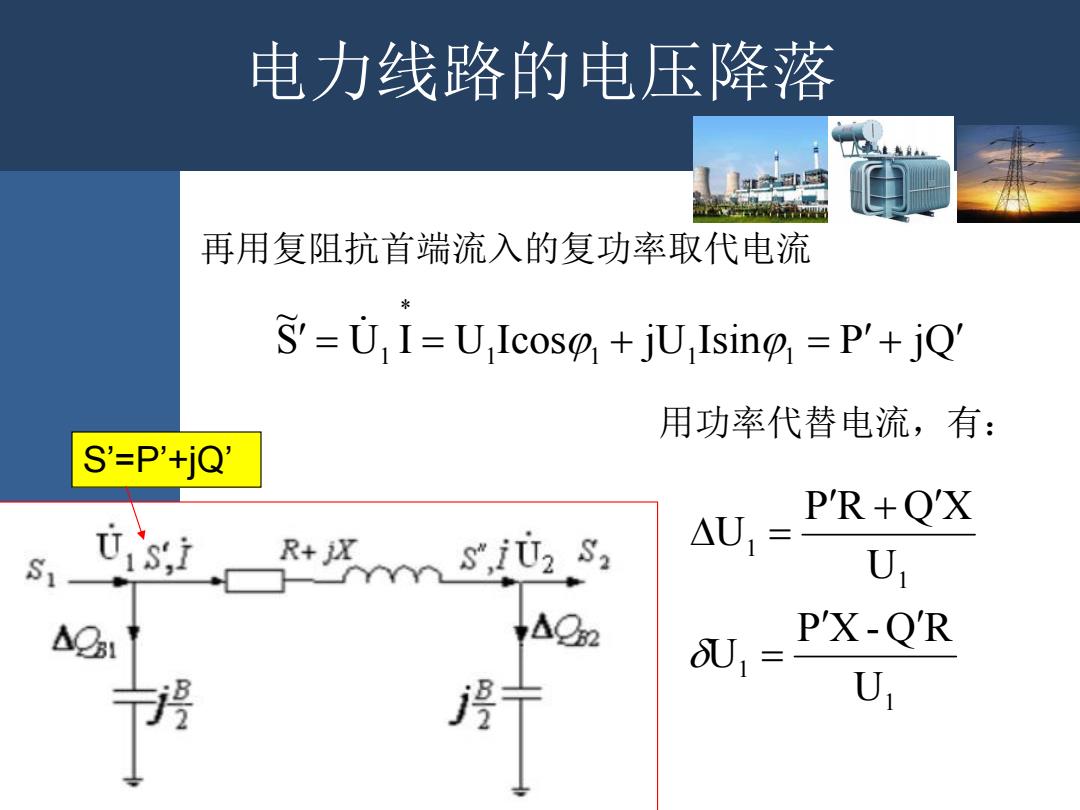
电力线路的电压降落 再用复阻抗首端流入的复功率取代电流 S=U I=U Icosp jU Ising =P'+jQ 用功率代替电流,有: S'=P'+jQ' AU PR+QX S U oUs X-QR U
电力线路的电压降落 再用复阻抗首端流入的复功率取代电流 用功率代替电流,有: 1 1 1 1 U P X -Q R U U P R Q X U S’=P’+jQ’ S U I U Icos jU Isin P jQ ~ 1 1 1 1 * 1

电力线路的电压降落 元件末端的相电压为 u=nX98U4-0 U U, U2=V(U,-AU2+(U,月 模 首末端的相位差
电力线路的电压降落 • 元件末端的相电压为 模 首末端的相位差 U - U P X - Q R - j U P R Q X U U - 2 1 1 2 1 1 1 1 2 1 2 2 1 1 U - U U arctan U U - U U

两种方法的比较 图3-3示出电压降落相量的两种不同的分 解。 计算电压降落的纵、横分量时,必须使 用同一点的功率和电压。 6i2 0 2 △U2
两种方法的比较 • 图3-3示出电压降落相量的两种不同的分 解。 • 计算电压降落的纵、横分量时,必须使 用同一点的功率和电压

讨论 在三相对称的电力系统中,若取R+X 仍为每相的复阻抗,S用三相功率 U、为线电压和线电流,则上述讨论 的得到的公式和结论也同样适用。 在本书的所有公式中,代表感性负荷 的无功功率时,其数值为正;代表容 性负荷的无功功率时,其数值为负
讨论 • 在三相对称的电力系统中,若取R+jX 仍为每相的复阻抗,S用三相功率, U、I为线电压和线电流,则上述讨论 的得到的公式和结论也同样适用。 • 在本书的所有公式中,代表感性负荷 的无功功率时,其数值为正;代表容 性负荷的无功功率时,其数值为负