
6.4在恒定磁场中电子的运动: 一.恒定磁场中的准经典运动 二.自由电子的量子理论 三. 晶体中电子的有效质量近似 四.回旋共振 五.霍尔效应 六.De Haas一Van Alphen效应 见黄昆书5.4;5.5;5.6节 讨论晶体电子在恒定磁场中的运动,是分析晶体许多重 要物理效应的理论基础,有两种方法:准经典近似和求解含 磁场的Schrδdinger方程,前一方法所得结果物理图像清晰, 但有一定的局限性。正确地解释这些现象是能带论的成功之 作,反之这些现象也成为能带论最有力的实验证据
6.4 在恒定磁场中电子的运动: 见黄昆书 5.4;5.5;5.6节 一. 恒定磁场中的准经典运动 二. 自由电子的量子理论 三. 晶体中电子的有效质量近似 四. 回旋共振 五. 霍尔效应 六. De Haas-Van Alphen效应 讨论晶体电子在恒定磁场中的运动,是分析晶体许多重 要物理效应的理论基础,有两种方法:准经典近似和求解含 磁场的Schrödinger方程,前一方法所得结果物理图像清晰, 但有一定的局限性。正确地解释这些现象是能带论的成功之 作,反之这些现象也成为能带论最有力的实验证据

一.恒定磁场中的准经典运动 依然沿用准经典运动的两个基本方程: 肉,E(侧 i jk -e vx Vy F=-ev(k)xB=方 B B B dt 只考虑磁场中的行为,公式中没有电场力,只有 Lorent忆力,磁场对电子的作用和电场不同,它不作功 不改变电子的能量。该公式表明,在只涉及外力时, 晶体动量起着普通动量的作用,我们假定只在z方向有 磁场,先在波矢空间下讨论B引och电子的行为
一. 恒定磁场中的准经典运动 依然沿用准经典运动的两个基本方程: ( ) ( ) = ( ) E e t = Ñ - ´ h h 1 d d k v k k k F v k B = { 只考虑磁场中的行为,公式中没有电场力,只有 Lorentz 力,磁场对电子的作用和电场不同,它不作功 不改变电子的能量。该公式表明,在只涉及外力时, 晶体动量起着普通动量的作用,我们假定只在z方向有 磁场,先在波矢空间下讨论Bloch电子的行为。 x y z x y z i j k e v v v B B B -
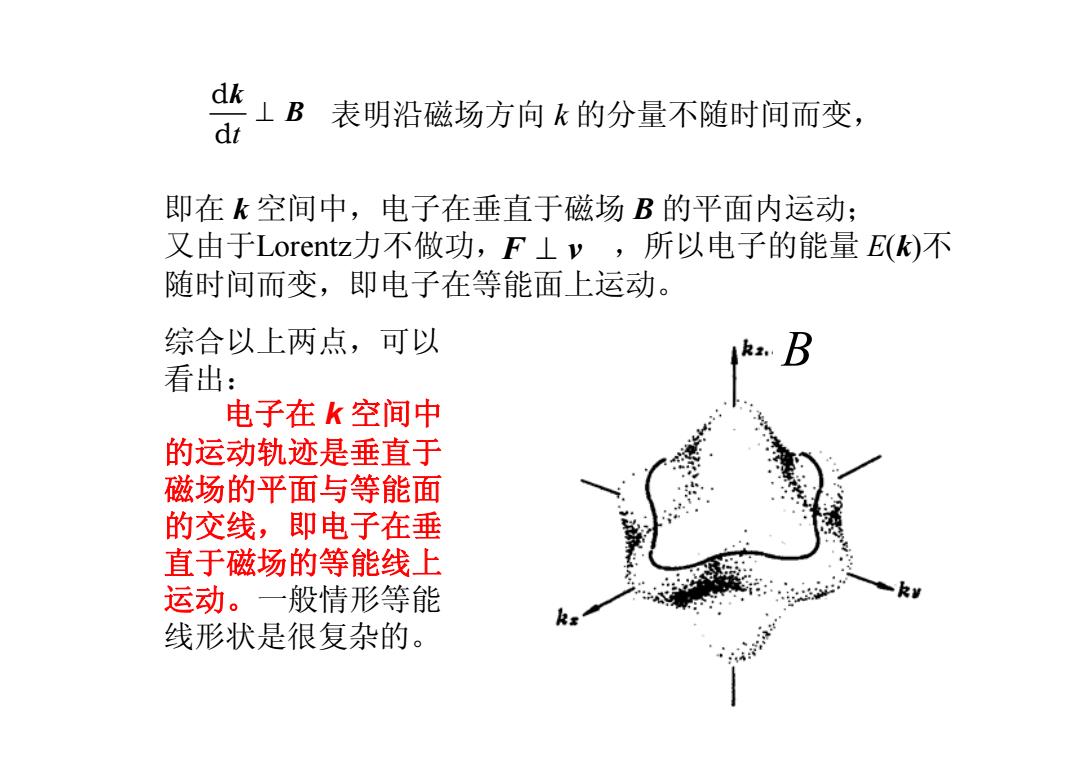
dk ⊥B 表明沿磁场方向k的分量不随时间而变, dt 即在k空间中,电子在垂直于磁场B的平面内运动; 又由于Lorentz力不做功,F⊥y,所以电子的能量E(k)不 随时间而变,即电子在等能面上运动。 综合以上两点,可以 看出: 电子在k空间中 的运动轨迹是垂直于 磁场的平面与等能面 的交线,即电子在垂 直于磁场的等能线上 运动。一般情形等能 线形状是很复杂的
t ^ d d k B 表明沿磁场方向 k 的分量不随时间而变, 即在 k 空间中,电子在垂直于磁场 B 的平面内运动; 又由于Lorentz力不做功, ,所以电子的能量 E(k)不 随时间而变,即电子在等能面上运动。 F v ^ 综合以上两点,可以 看出: 电子在 k 空间中 的运动轨迹是垂直于 磁场的平面与等能面 的交线,即电子在垂 直于磁场的等能线上 运动。一般情形等能 线形状是很复杂的。 B
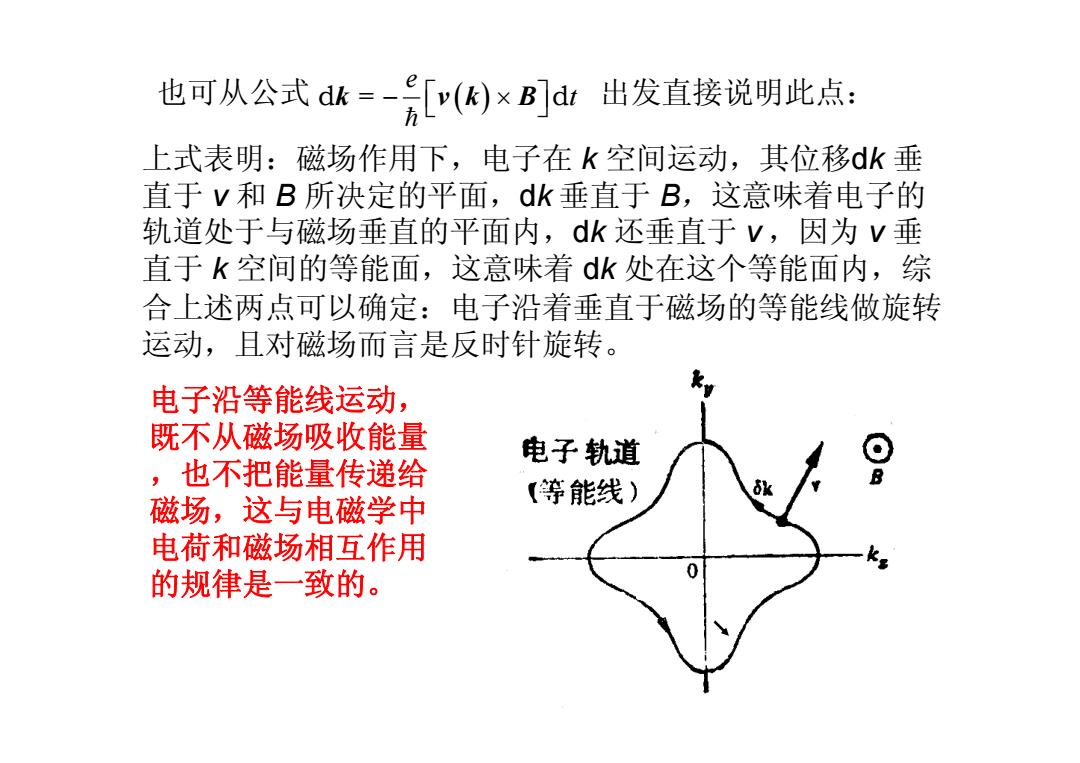
也可从公式dk=[()×B]d出发直接说明此点: 上式表明:磁场作用下,电子在k空间运动,其位移dk垂 直于V和B所决定的平面,dk垂直于B,这意味着电子的 轨道处于与磁场垂直的平面内,dk还垂直于V,因为v垂 直于k空间的等能面,这意味着dk处在这个等能面内,综 合上述两点可以确定:电子沿着垂直于磁场的等能线做旋转 运动,且对磁场而言是反时针旋转。 电子沿等能线运动, 既不从磁场吸收能量 电子轨道 ,也不把能量传递给 磁场,这与电磁学中 等能线) 电荷和磁场相互作用 的规律是一致的
( ) e = t - é ´ ù ë û h 也可从公式 d d k v k B 出发直接说明此点: 上式表明:磁场作用下,电子在 k 空间运动,其位移dk 垂 直于 v 和 B 所决定的平面,dk 垂直于 B,这意味着电子的 轨道处于与磁场垂直的平面内,dk 还垂直于 v ,因为 v 垂 直于 k 空间的等能面,这意味着 dk 处在这个等能面内,综 合上述两点可以确定:电子沿着垂直于磁场的等能线做旋转 运动,且对磁场而言是反时针旋转。 电子沿等能线运动, 既不从磁场吸收能量 ,也不把能量传递给 磁场,这与电磁学中 电荷和磁场相互作用 的规律是一致的

如图所示电子在k空间中的运动是循环的,经过一段时间 后又回到出发的那一点。按照上式: 电子回旋运动周期: dk dk E=const v取垂直于磁场的分量。 回旋运动圆频率(Cyclotron frequency): 2元 0。= =2πeB T dk E=const 这里,微分dk是沿回路周边取的,一般情况形状复杂
电子回旋运动周期: 回旋运动圆频率(Cyclotron frequency): const const const d d d E E E k k T t eB v = = = k ^ = = = ò ò ò v v h w Ñ Ñ Ñ & v 取垂直于磁场的分量。 const 2 2 d c E eB T k v p w p = ^ = = ò v h Ñ 如图所示电子在 k 空间中的运动是循环的,经过一段时间 后又回到出发的那一点。按照上式: 这里,微分dk 是沿回路周边取的,一般情况形状复杂