《信息论与编码》课程教学资源（作业习题）第三章 信道与信道容量（含解答）

X1「x X2 3-1设有一离散无记忆信源，其概率空间为 信源发出符号通过 P(x) 0.60.4 1) 一干扰信道，接收符号为Y={以，y2}，信道传递矩阵为P= 6 6 求： 3 4) (1)信源X中事件x和x,分别含有的自信息量： (2)收到消息y,(=1,2)后，获得的关于x(i=1,2)的信息量： (3)信源X和信宿Y的信息熵： (4)信道疑义度H(X/Y)和噪声熵H(Y/X): (5)接收到消息Y后获得的平均互信息量I(X;Y)。 解：(1)I(x)=0.737bit,1(x2)=1.322bit (2）I(xy)=0.474bit,I(x2)=-1.263bit,I(x2;y)=-1.263bit, I(x2;2)=0.907bit (3)H(X)=H(0.6,0.4)=0.971bit1 symbol HY)=H(0.6,0.4)=0.971bit/symbol (4)H(XY)=H(0.5,0.1,0.1,0.3)=1.685bit/symbol H(X/Y)=1.685-0.971=0.714bit/symbol H(Y/X)=0.714 bit symbol (5)I(X;Y)=0.971-0.714=0.257bit/symbol 3-2设有扰离散信道的输入端是以等概率出现的A、B、C、D四个字母。该信道的正 确传输概率为0.5，错误传输概率平均分布在其他三个字母上。验证在该信道上每个字母传 输的平均信息量为0.21比特。 证明：信道传输矩阵为：

3-1 设有一离散无记忆信源，其概率空间为 1 2 ( ) 0.6 0.4 X x x P x              ，信源发出符号通过 一干扰信道，接收符号为 1 2 Y y y  { , } ，信道传递矩阵为 5 1 6 6 1 3 4 4 P        ，求： （1） 信源 X 中事件 1 x 和 2 x 分别含有的自信息量； （2） 收到消息 j y （j＝1，2）后，获得的关于 i x （i＝1，2）的信息量； （3） 信源 X 和信宿Y 的信息熵； （4） 信道疑义度 H X Y ( / ) 和噪声熵 H Y X ( / ) ； （5） 接收到消息Y 后获得的平均互信息量 I X Y ( ; ) 。 解：（1） 1 2 I x bit I x bit ( ) 0.737 , ( ) 1.322   （ 2 ） 1 1 I x y bit ( ; ) 0.474  ， 1 2 I x y bit ( ; ) 1.263   ， 2 1 I x y bit ( ; ) 1.263   ， 2 2 I x y bit ( ; ) 0.907  （3） H X H bit symbol ( ) (0.6,0.4) 0.971 /   H Y H bit symbol ( ) (0.6,0.4) 0.971 /   （4） H XY H bit symbol ( ) (0.5,0.1,0.1,0.3) 1.685 /   H X Y bit symbol ( / ) 1.685 0.971 0.714 /    H Y X bit symbol ( / ) 0.714 /  （5） I X Y bit symbol ( ; ) 0.971 0.714 0.257 /    3-2 设有扰离散信道的输入端是以等概率出现的 A、B、C、D 四个字母。该信道的正 确传输概率为 0.5，错误传输概率平均分布在其他三个字母上。验证在该信道上每个字母传 输的平均信息量为 0.21 比特。 证明：信道传输矩阵为：

1 11 2 6 6 1-6 6 1-6 P= 6 1 信源信宿概率分布为：P(X)=P(Y)={ 1111 1 1 4444 6 6 2 6 1 6 6 6 2 H(YX)=1.79(bit/符号)，IX,Y)=H(Y)-H(Y/X)=2-1.79=0.21(bit/符号) 3-3己知信源X包含两种消息：X1,x2,且P(x)=P(x2)=1/2,信道是有扰的，信 0.980.02 宿收到的消息集合Y包含1,2。给定信道矩阵为：P= 求平均互信息 0.20.8 I(X;Y)。 解：I(XY)=H(X)+H(Y)-H(XY) H(X)=1bit/符号，H(Y)=0.93bit/符号，H(XY)=1.34bit/符号，I(X;Y)=0.59bit/符号。 2 1 3-4设二元对称信道的传递矩阵为： 3 (1)若PO-3,PI=,求HX,HK1Y,H1X)和1X, 4 4 (2)求该信道的信道容量及其达到信道容量时的输入概率分布。 解：(1)HX)=0.811(bit/符号)，HXY)=1.73(bit/符号)，H(Y)=0.98(bit/符号)， H(XN)=0.75(bit/符号)，H(Y/X)=0.92(bit/符号)，I(X:Y)=0.06(bit/符号)； (2)C=002(bm符号)，最佳输入分布为：R=兮 3-5求下列两个信道的信道容量，并加以比较： p-Ep-628 p-8 0 (1) (2) p-62 p-8 p-628 D-8 p-802 其中p+p=1。 解：(1) C,=log2-H(p-6,p-6,28)-(1-28)log1-2)-2slog48 =1+(p-)log(p-e)+(p-6)log(p-)+2clog26-(1-26)log(1-26)-2εlog48 =1-2e+(p-)log(p-8)+(p-)log(p-)-(1-2e)1log(1-2e) (2)

1 1 1 1 2 6 6 6 1 1 1 1 6 2 6 6 1 1 1 1 6 6 2 6 1 1 1 1 6 6 6 2 P        ，信源信宿概率分布为： 1 1 1 1 ( ) ( ) { , , , } 4 4 4 4 P X P Y   ， H(Y/X)=1.79（bit/符号），I(X;Y)=H(Y)- H(Y/X)=2-1.79=0.21（bit/符号） 3-3 已知信源 X 包含两种消息： 1 2 x x, ，且 1 2 P x P x ( ) ( ) 1/ 2   ，信道是有扰的，信 宿收到的消息集合Y 包含 1 2 y y, 。给定信道矩阵为： 0.98 0.02 0.2 0.8 P        ，求平均互信息 I X Y ( ; ) 。 解：I(X;Y)=H(X)+H(Y)-H(XY) H(X)=1 bit/符号,H(Y)=0.93 bit/符号,H(XY)=1.34 bit/符号, I(X;Y)=0.59 bit/符号。 3-4 设二元对称信道的传递矩阵为： 2 1 3 3 1 2 3 3       ， （1） 若P(0)= 3 4 ，P(1)= 1 4 ，求 H X( ) ， H X Y ( / ) ， H Y X ( / ) 和 I X Y ( ; ) ； （2） 求该信道的信道容量及其达到信道容量时的输入概率分布。 解：（1）H(X)=0.811（bit/符号），H(XY)=1.73（bit/符号），H(Y)=0.98（bit/符号）， H(X/Y)=0.75（bit/符号），H(Y/X)=0.92（bit/符号），I(X；Y)=0.06（bit/符号）； （2）C＝0.082（bit/符号），最佳输入分布为： 1 1 { } 2 2 PX  3-5 求下列两个信道的信道容量，并加以比较： （1） 2 2 p p p p                 （2） 2 0 0 2 p p p p                 其中 p p  1。 解：（1） 1 log 2 ( , ,2 ) (1 2 )log(1 2 ) 2 log 4 1 ( )log( ) ( )log( ) 2 log 2 (1 2 )log(1 2 ) 2 log 4 1 2 ( )log( ) ( )log( ) (1 2 )log(1 2 ) C H p p p p p p p p p p                                                        （2）

C2=log2-H(p-6,p-6,2e)-(1-2e)log1-28)-2elog28 =1+(p-s)log(p-s)+(p-s)log(p-s)+2slog26-(1-25)log(1-2s)-2slog2s =1+(p-)log(p-e)+(p-6)log(p-)-(1-2ε)log1-28) 两者的信道容量比较：C,=C+28 3-6求题图3-6中信道的信道容量及最佳的输入概率分布。并求当ε=0和二时的信道容 量C。 0 0 1-8 2 1-6 题图3-6 解：由图知信道转移矩阵为： [10 0 P=01-88 此信道非对称信道，也非准对称信道，不能利用其公式计算。 10 1-6 此信道也不能采用先假设一种输入分布，利用信道容量解的充要性来计算。但此信道矩阵是 非奇异矩阵，又x=S,则可利用方程组求解： ,a)pa)lo P)12. B=0 (1-6)p2+e3=(1-e)log1-8)+slog6 p2+(1-)B3=(1-)log1-)+elog8 解得：阝=0，B2=阝3=(1-)1og(1-)+log6,所以 C=log >2=log[1+2-M(], p(6)=2A-c=2-,pb,)=2-c=2-Hec,p(b)=2%-c=2eC, 根据P(b,)=∑P(a,)P(b,1a),j=1,2,3,得最佳输入分布为： p(a)-=p6)=2c,p(a)=p(a)=p(b,)=p()-2s-c, 当6=0时，此信道为一一对应信道

2 log 2 ( , ,2 ) (1 2 )log(1 2 ) 2 log 2 1 ( )log( ) ( )log( ) 2 log 2 (1 2 )log(1 2 ) 2 log 2 1 ( )log( ) ( )log( ) (1 2 )log(1 2 ) C H p p p p p p p p p p                                                      两者的信道容量比较： 2 1 C C  2 3-6 求题图3-6中信道的信道容量及最佳的输入概率分布。并求当  0 和 1 2 时的信道容 量C。 题图 3-6 解：由图知信道转移矩阵为： 1 0 0 0 1 0 1 P              ，此信道非对称信道，也非准对称信道，不能利用其公式计算。 此信道也不能采用先假设一种输入分布，利用信道容量解的充要性来计算。但此信道矩阵是 非奇异矩阵，又r＝s，则可利用方程组求解： 3 3 1 1 ( / ) ( / )log ( / ), 1,2,3 j i j j i j i j j P b a P b a P b a i       ，所以 1 2 3 2 3 0 (1 ) (1 )log(1 ) log (1 ) (1 )log(1 ) log                                  解得： 1   0 ， 2 3            (1 )log(1 ) log ，所以 1 ( ) log 2 log[1 2 ] j H j C        ， 1 1 ( ) 2 2 C C p b      ， 2 ( ) 2 ( ) 2 2 C H C p b        ， 3 ( ) 3 ( ) 2 2 C H C p b        ， 根据 3 1 ( ) ( ) ( / ), 1, 2,3 j i j i i P b P a P b a j     ，得最佳输入分布为： 1 1 ( ) ( ) 2 C p a p b    ， ( ) 2 3 2 3 ( ) ( ) ( ) ( ) 2 H C p a p a p b p b        ， 当 ＝0时，此信道为一一对应信道

C=log3.p(a)=p(az)=P(a;)=3 当E=0.5时，C=log2,pa)=2pa)=pa)=4 0.980.02 3-7有一个二元对称信道，其信道矩阵为 。 设该信道以1500个二元符号 0.020.98 每秒的速率传输输入符号。现有一消息序列共有14000个二元符号，并设在这个消息中， P(0)=P(①)=1/2。问从信息传输的角度来考虑，10秒内能否将这消息序列无失真地传送 完？ 解：信道容量：C=0.859(bit/符号)，C,=1500×0.859=1288(bit/s),10秒内最大 信息传输能力=12880bits,消息序列含有信息量=14000bits, 12880<14000,所以10秒内不能将这消息序列无失真地传送完。 3-8有一离散信道，其信道转移概率如题图3-8所示，试求： (1)信道容量C: (2)若62=0，求信道容量。 1-61-E2 0 0 1-61-62 题图3-8 解：1C=-0-6l0g'2+6lg+0-台-)ogl-6-6) (2)若62=0，则C=1-6 3-9设离散信道矩阵为： 11 1 3 P= 3 6 1 1 6 6 3 求信道容量C。 解：C=0.041(bit/符号)。 3-10若有一离散非对称信道，其信道转移概率如题图3-10所示。试求：

1 2 3 1 log 3, ( ) ( ) ( ) 3 C p a p a p a     ； 当 ＝0.5时， 1 2 3 1 1 log 2, ( ) , ( ) ( ) 2 4 C p a p a p a     。 3-7 有一个二元对称信道，其信道矩阵为 0.98 0.02 0.02 0.98       。设该信道以 1500 个二元符号 每秒的速率传输输入符号。现有一消息序列共有 14000 个二元符号，并设在这个消息中， P P (0) (1) 1/ 2   。问从信息传输的角度来考虑，10 秒内能否将这消息序列无失真地传送 完？ 解：信道容量：C＝0.859（bit/符号）， 1500 0.859 1288( / ) C bit s t    ，10秒内最大 信息传输能力＝12880 bits，消息序列含有信息量＝14000 bits， 12880<14000，所以10秒内不能将这消息序列无失真地传送完。 3-8 有一离散信道，其信道转移概率如题图3-8所示，试求： （1） 信道容量C； （2） 若 2  ＝0，求信道容量。 题图 3-8 解：（1） 1 1 2 2 1 2 1 2 1 (1 )log log (1 )log(1 ) 2 C                   （2）若 2   0 ，则 1 C  1  3-9 设离散信道矩阵为： 1 1 1 1 3 3 6 6 1 1 1 1 6 3 6 3 P        ， 求信道容量C。 解：C＝0.041（bit/符号）。 3-10 若有一离散非对称信道，其信道转移概率如题图3-10所示。试求：

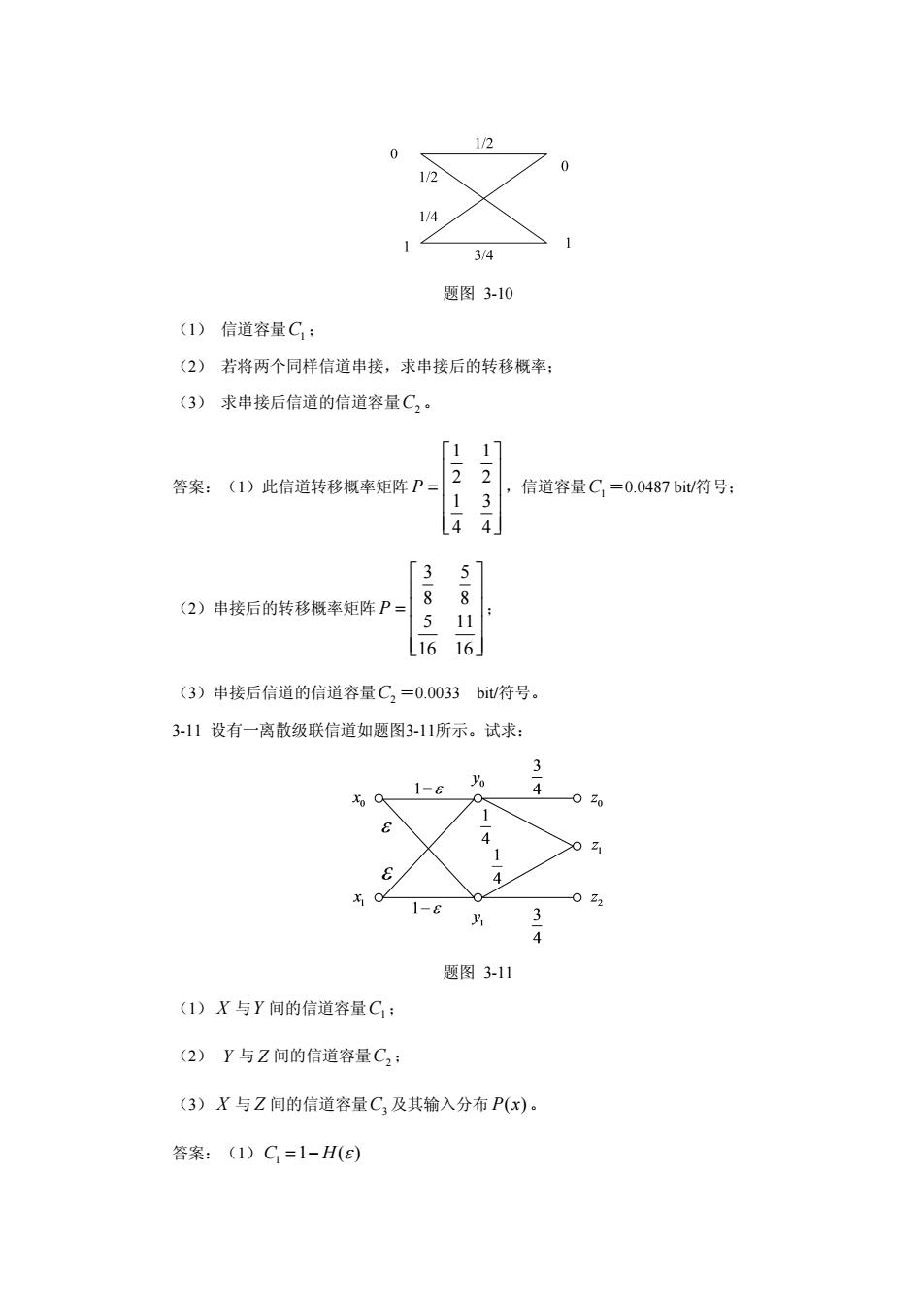
0 1/2 0 1/2 1/4 3/4 题图3-10 (1) 信道容量C: (2)若将两个同样信道串接，求串接后的转移概率： (3)求串接后信道的信道容量C2。 「1 17 答案：(1)此信道转移概率矩阵P= 2 2 信道容量C,=0.0487bit/符号： 3 5 (2)串接后的转移概率矩阵P= 8 8 11 16 16 (3)串接后信道的信道容量C,=0.0033bit/符号。 3-11设有一离散级联信道如题图3-11所示。试求： 3 1-e 4 020 1 4 1 0Z1 & x 1-6 0z2 y 3 题图3-11 (1)X与Y间的信道容量C: (2)Y与Z间的信道容量C2: (3)X与Z间的信道容量C3及其输入分布P(x)。 答案：(1)C=1-H(s)

题图 3-10 （1） 信道容量C1 ； （2） 若将两个同样信道串接，求串接后的转移概率； （3） 求串接后信道的信道容量C2 。 答案：（1）此信道转移概率矩阵 1 1 2 2 1 3 4 4 P        ，信道容量C1 ＝0.0487 bit/符号； （2）串接后的转移概率矩阵 3 5 8 8 5 11 16 16 P        ； （3）串接后信道的信道容量C2 ＝0.0033 bit/符号。 3-11 设有一离散级联信道如题图3-11所示。试求： 题图 3-11 （1） X 与Y 间的信道容量C1 ； （2） Y 与 Z 间的信道容量C2 ； （3） X 与 Z 间的信道容量C3 及其输入分布 P x( ) 。 答案：（1） 1 C H  1 ( ) 