
实验一绘制二进熵函数曲线 一、实验目的: 1.掌握Matlab绘图函数 2.掌握、理解熵函数表达式及其性质 二、实验要求: 1.提前预习实验,认真阅读实验原理以及相应的参考书。 2.在实验报告中给出二进制熵函数曲线图 三、实验原理: 1.信源熵的概念及性质 「x1_x=032= PX)p ,0≤p≤1 1-p H(X)=-∑p(x)Iogp(x) =-[plogp+(1-p)log(1-p) =H(p) a.H(X)≤logn b.H[P+1-)g]≥H(P)+(1-)H(g) 四、实验内容: 用Matlab软件制作二进熵函数曲线
实验一 绘制二进熵函数曲线 一、实验目的: 1. 掌握 Matlab 绘图函数 2. 掌握、理解熵函数表达式及其性质 二、实验要求: 1. 提前预习实验,认真阅读实验原理以及相应的参考书。 2. 在实验报告中给出二进制熵函数曲线图 三、实验原理: 1. 信源熵的概念及性质 . 1 ( ) 1 ( ) . ( ) log ( ) log 1 log 1 ( ) ( )log ( ) , 0 1 1 0 1 ( ) 1 2 b H P Q H P H Q a H X n H p p p p p H X p x p x p p p x x P X X i i i 四、实验内容: 用 Matlab 软件制作二进熵函数曲线

实验二:luffman编码软件实现 1、实验目的 (1)进一步熟悉Huffman编码过程: (2)掌握C语言递归程序的设计和调试技术(或者使用Matlab)。 2、实验要求 (1)输入:信源符号个数r、信源的概率分布P: (2)输出:每个信源符号对应的Huffman编码的码字。 3、实验内容 (1)算法 1、从键盘输入组成信源C的字符个数N: 2、从键盘输入信源C和组成信源的字符所对应的概率数组P: 3、用Huffman函数来对信源进行二进制编码;先对P按从大到小进行排序, 与此同时要把C中相应的字符的位置做相应的调换;用comt数组来记录编码: 在进行记录编码时是从数组cot的最后一个开始存储的,而且,每进行一次编 码所记录下来的两个编码0,1'是按从数组的最后一个元素开始服从 count[m-k-j]、count[m-k-j-l],其中k表示编码所进行的次数,j表示每次编码都 只有'0,T";最后用函数print(0来输出编码。 (2)部分伪代码: (一)节点信息结构体 struct HuffNode int weight;:/∥信源符号的概率 int parent; int lchild; int rchild: }; (二)算法 void Huffman(int weight[],int n,HuffNode hn[],HuffCode hc[]) { for(i=0;i!=2*n-1;++i)//create Huffman Node,step 1 {0} for(i=0;i !=n-1;++i)//create Huffman Node,step 2
实验二:Huffman 编码软件实现 1、实验目的 (1)进一步熟悉 Huffman 编码过程; (2)掌握 C 语言递归程序的设计和调试技术(或者使用 Matlab)。 2、实验要求 (1)输入:信源符号个数 r、信源的概率分布 P; (2)输出:每个信源符号对应的 Huffman 编码的码字。 3、实验内容 (1)算法 1、从键盘输入组成信源 C 的字符个数 N; 2、从键盘输入信源 C 和组成信源的字符所对应的概率数组 P; 3、用 Huffman函数来对信源进行二进制编码;先对 P 按从大到小进行排序, 与此同时要把 C 中相应的字符的位置做相应的调换;用count 数组来记录编码: 在进行记录编码时是从数组count 的最后一个开始存储的,而且,每进行一次编 码 所 记 录 下 来 的 两 个 编 码 '0','1' 是 按 从 数 组 的 最 后 一 个 元 素 开 始 服 从 count[m-k-j]、count[m-k-j-1],其中 k 表示编码所进行的次数,j 表示每次编码都 只有'0','1';最后用函数 print() 来输出编码。 (2)部分伪代码: (一)节点信息结构体 struct HuffNode { int weight;//信源符号的概率 int parent; int lchild; int rchild; }; (二)算法 void Huffman(int weight[], int n, HuffNode hn[], HuffCode hc[]) { for(i = 0; i != 2*n - 1; ++i) //create Huffman Node,step 1 {} for(i = 0; i != n-1; ++i) //create Huffman Node, step 2 {

for(j=0;j!=n+i;j++) if(hn[j].weight minl &hn[j].parent =0) {} else if(hn[j].weight min2 &hn[j].parent =0) else; } 在此逆序存储luffman编码 int temp[maxlen]; for(i=0;i!=n;++i) { int parent hn[i].parent; while(hn[child].parent !=0) 公 4、实验报告 (1)简要总结Huffman编码的原理与特点 (2)写出Huffman编码的基本步骤,画出实现Huffman编码的程序流程图 (3)给出Huffman编码的源程序,并给出实验过程中的测试结果 (4)总结实验过程遇到的问题及解决方法
for(j = 0; j != n+i; j++) { if(hn[j].weight < min1 && hn[j].parent == 0) {} else if(hn[j].weight < min2 && hn[j].parent == 0) {}else ; }} 在此逆序存储 Huffman 编码 int temp[maxlen]; for(i = 0; i != n; ++i) { int parent = hn[i].parent; while(hn[child].parent != 0) {} 4、实验报告 (1)简要总结 Huffman 编码的原理与特点 (2)写出 Huffman 编码的基本步骤,画出实现 Huffman 编码的程序流程图 (3)给出 Huffman 编码的源程序,并给出实验过程中的测试结果 (4)总结实验过程遇到的问题及解决方法

实验三循环码的编码和译码程序设计 一、实验目的: 1.通过实验了解循环码的工作原理。 2.了解生成多项式(x)与编码、译码的关系。 3.了解码距d与纠、检错能力之间的关系。 4.分析(7.3)循环码的纠错能力。 二、实验要求: 1、编、译码用上述的计算法程序框图编写。 2、计算出所有的码字集合,可纠错误图样E(x)表和对应的错误伴随式表。 3、考查和分析该码检、纠一、二位错误的能力情况。 4、整理好所有的程序清单,变量名尽量用程序框图所给名称,并作注释。 5、出示软件报告 三、实验设计原理 1、循环码编码原理 设有一(n,k)循环码,码字C=[Cn-1.CrCr-1.C0],其中=n-k。码 字多项式为: C(x)=Cn-1xn-1+Cn-2xn-2+.C1x+C0。 码字的生成多项式为:g(x)=gr-1xr-lgr-2xr-2++g1lx+g0 待编码的信息多项式为:m(x)=mK-1xK-1++m0 xn-k.m (x)=Cn-1xn-1+.+Cn-Kxn-K 对于系统码有: Cn-1=mK-1,Cn-2=mK-2,.Cn-K=Cr=m0 设监督多项式为: r (x)=Cr-1Xr-1+.+C1x+C0 根据循环码的定义,则有: C (x)=xn-Km (x)+r (x)=q (x).g(x) Xn-Km(x)=q(x).g(x)+r(x) r(x)=Rg(x)[xn-Km(x)] 即监督多项式是将多项式xn-Km(x)除以g(x)所得的余式。 编码过程就是如何根据生成多项式完成除法运算求取监督多项式的过程。 设循环码(7.3)码的字多项式为: C(x)-C6x6+C5x5+C4x4+C3x3+C2x2C1x+C0 (n=7) 生成多项式为: g(x)=x4+x2+x+1 信息多项式为: m(x)=m2x2+mlx+m0 (k=3), 设 m(x)=x2+x 监督多项式为: r(x)=Cr-1Xr-1+.+C1x+CO 根据循环码的定义:生成多项式的倍式均是码字,编码实际上是做xn-km(x) 除以g(x)的 运算求得(x)。 编码程序框图见图4.1(a)左,二进制多项式除法示意图见图4.1(b)。 2、译码原理
实验三 循环码的编码和译码程序设计 一、实验目的: 1.通过实验了解循环码的工作原理。 2.了解生成多项式 g(x)与编码、译码的关系。 3.了解码距 d 与纠、检错能力之间的关系。 4.分析(7.3)循环码的纠错能力。 二、实验要求: 1、编、译码用上述的计算法程序框图编写。 2、计算出所有的码字集合,可纠错误图样 E(x)表和对应的错误伴随式表。 3、考查和分析该码检、纠一、二位错误的能力情况。 4、整理好所有的程序清单,变量名尽量用程序框图所给名称,并作注释。 5、出示软件报告. 三、实验设计原理 1、循环码编码原理 设有一(n,k)循环码,码字C=[Cn-1.CrCr-1.C0],其中 r=n-k。码 字多项式为: C(x)= Cn-1xn-1+Cn-2xn-2+.C1x+C0。 码字的生成多项式为: g(x)=gr-1xr-1gr-2xr-2+.+g1x+g0 待编码的信息多项式为: m(x)=mK-1xK-1+.+m0 xn-k.m(x)=Cn-1xn-1+.+Cn-Kxn-K 对于系统码有: Cn-1=mK-1,Cn-2=mK-2,.Cn-K=Cr=m0 设监督多项式为: r(x)=Cr-1Xr-1+.+C1x+C0 根据循环码的定义,则有: C(x)=xn-Km(x)+r(x)=q(x).g(x) Xn-Km(x)=q(x).g(x)+r(x) r(x)=Rg(x)[xn-Km(x)] 即监督多项式是将多项式 xn-Km(x)除以 g(x)所得的余式。 编码过程就是如何根据生成多项式完成除法运算求取监督多项式的过程。 设循环码(7.3)码的字多项式为: C(x)=C6x6+C5x5+C4x4+C3x3+C2x2C1x+C0 (n=7) 生成多项式为: g(x)=x4+x2+x+1 信息多项式为: m(x)=m2x2+m1x+m0 (k=3), 设 m(x)=x2+x 监督多项式为: r(x)= Cr-1Xr-1+.+C1x+C0 根据循环码的定义:生成多项式的倍式均是码字,编码实际上是做 xn- km(x) 除以 g(x)的 运算求得 r(x)。 编码程序框图见图 4.1(a)左,二进制多项式除法示意图见图 4.1(b)。 2、译码原理
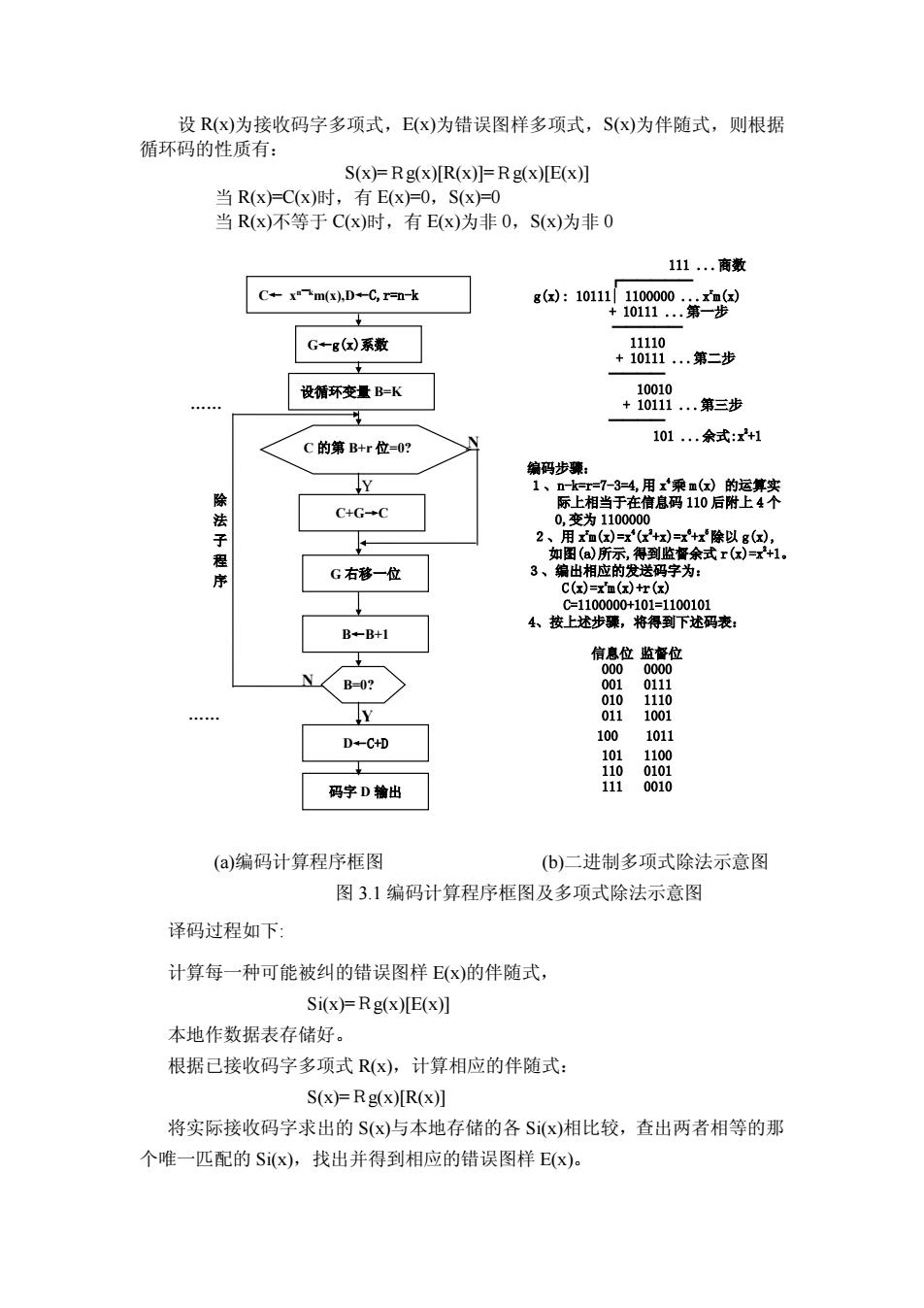
设R(x)为接收码字多项式,E(x)为错误图样多项式,S(x)为伴随式,则根据 循环码的性质有: S(x)=Rg(x)[R(x)]=Rg(x)[E(x)] 当R(x)=C(x)时,有E(x)=0,S(x)=0 当R(x)不等于C(x)时,有E(x)为非0,S(x)为非0 111.商数 C+xm(x).D+C,r=n-k g(x):101111100000:.xm(x) +10111.第一步 G-g(x)系数 11110 +10111 .第二步 设循环变量B=K 10010 +10111.第三步 101.余式:x+1 C的第B+r位=0? 编码步骤: Y 1、n-k-r=7-3=4,用x乘m(x)的运算实 除 际上相当于在信息码110后附上4个 C+G→C 0,变为1100000 2、用x血(x)=x(x+x=x+x除以gx, 程 如图(a)所示,得到监督余式r(x)=x+1。 序 G右移一位 3、编出相应的发送码字为: C(x)=x'm(x)+r(x) C1100000+101=1100101 4、按上述步躁,将得到下述码表: B+B+1 信息位监督位 000 0000 001 0111 010 1110 011 1001 D+C+D 100 1011 101 1100 110 0101 码字D输出 111 0010 (a)编码计算程序框图 (b)二进制多项式除法示意图 图3.1编码计算程序框图及多项式除法示意图 译码过程如下: 计算每一种可能被纠的错误图样Ex)的伴随式, Si(x)=Rg(x)[E(x)] 本地作数据表存储好。 根据已接收码字多项式R(x),计算相应的伴随式: S(x)=Rg(x)[R(x)] 将实际接收码字求出的S(x)与本地存储的各Si(x)相比较,查出两者相等的那 个唯一匹配的S(x),找出并得到相应的错误图样E(x)
设 R(x)为接收码字多项式,E(x)为错误图样多项式,S(x)为伴随式,则根据 循环码的性质有: S(x)=Rg(x)[R(x)]=Rg(x)[E(x)] 当 R(x)=C(x)时,有 E(x)=0,S(x)=0 当 R(x)不等于 C(x)时,有 E(x)为非 0,S(x)为非 0 (a)编码计算程序框图 (b)二进制多项式除法示意图 图 3.1 编码计算程序框图及多项式除法示意图 译码过程如下: 计算每一种可能被纠的错误图样 E(x)的伴随式, Si(x)=Rg(x)[E(x)] 本地作数据表存储好。 根据已接收码字多项式 R(x),计算相应的伴随式: S(x)=Rg(x)[R(x)] 将实际接收码字求出的 S(x)与本地存储的各 Si(x)相比较,查出两者相等的那 个唯一匹配的 Si(x),找出并得到相应的错误图样 E(x)。 111 .商数 ┌───── g(x): 10111| 1100000 .x rm(x) + 10111 .第一步 ───── 11110 + 10111 .第二步 ──── 10010 + 10111 .第三步 ──── 101 .余式:x 2+1 编码步骤: 1、n-k=r=7-3=4,用 x 4乘 m(x)的运算实 际上相当于在信息码 110 后附上 4 个 0,变为 1100000 2、用 x rm(x)=x4(x2+x)=x6+x5除以 g(x), 如图(a)所示,得到监督余式 r(x)=x2+1。 3、编出相应的发送码字为: C(x)=xrm(x)+r(x) C=1100000+101=1100101 4、按上述步骤,将得到下述码表: 信息位 监督位 000 0000 001 0111 010 1110 011 1001 100 1011 101 1100 110 0101 111 0010 . . 除 法 子 程 序 N N Y Y C← x n—km(x),D←C,r=n-k G←g(x)系数 设循环变量 B=K C 的第 B+r 位=0? C+G→C G 右移一位 B←B+1 B=0? D←C+D 码字 D 输出