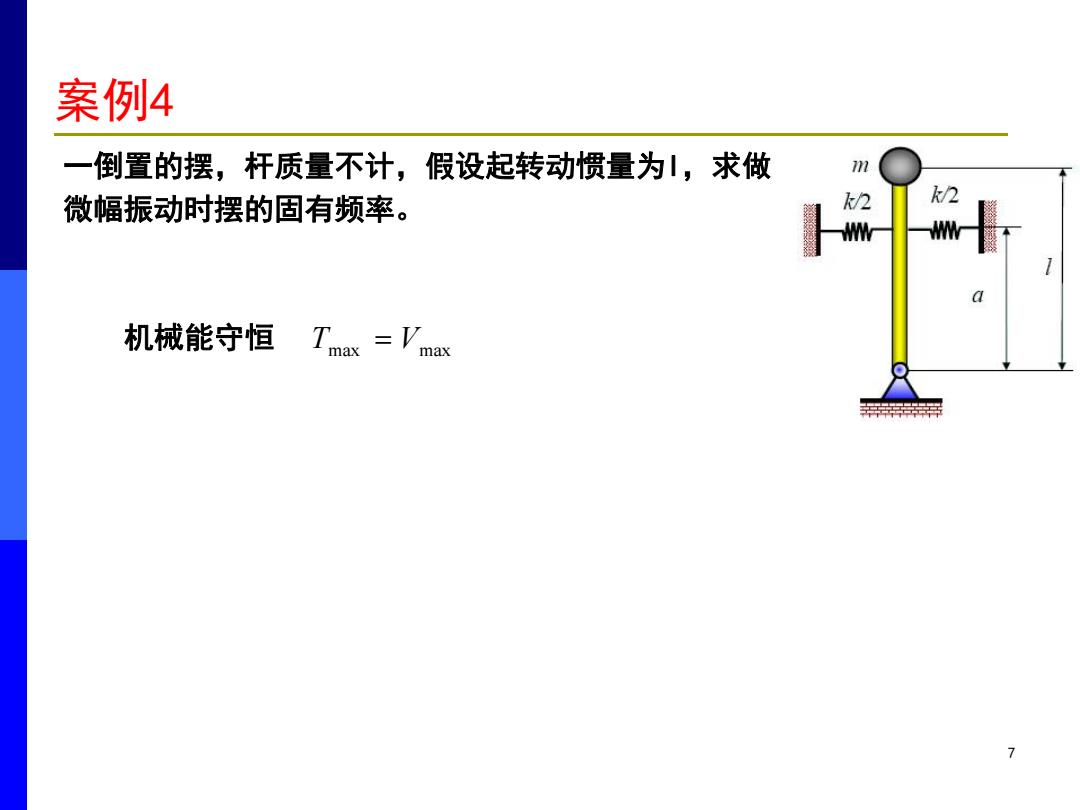
案例4 一倒置的摆,杆质量不计,假设起转动惯量为,求做 m 微幅振动时摆的固有频率。 2 k/2 机械能守恒 T'max =V max 7
7 一倒置的摆,杆质量不计,假设起转动惯量为I,求做 微幅振动时摆的固有频率。 机械能守恒 Tmax Vmax 案例4
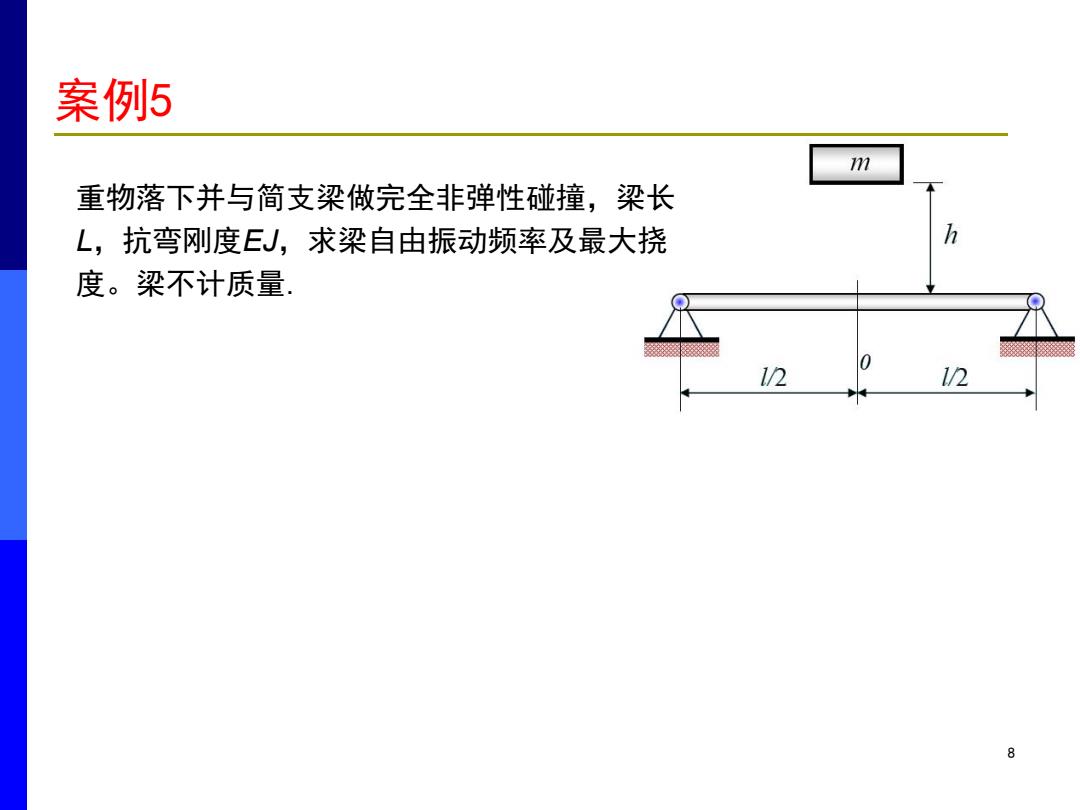
案例5 m 重物落下并与简支梁做完全非弹性碰撞,梁长 L,抗弯刚度EJ,求梁自由振动频率及最大挠 度。梁不计质量 12 12 8
8 重物落下并与简支梁做完全非弹性碰撞,梁长 L,抗弯刚度EJ,求梁自由振动频率及最大挠 度。梁不计质量. 案例5
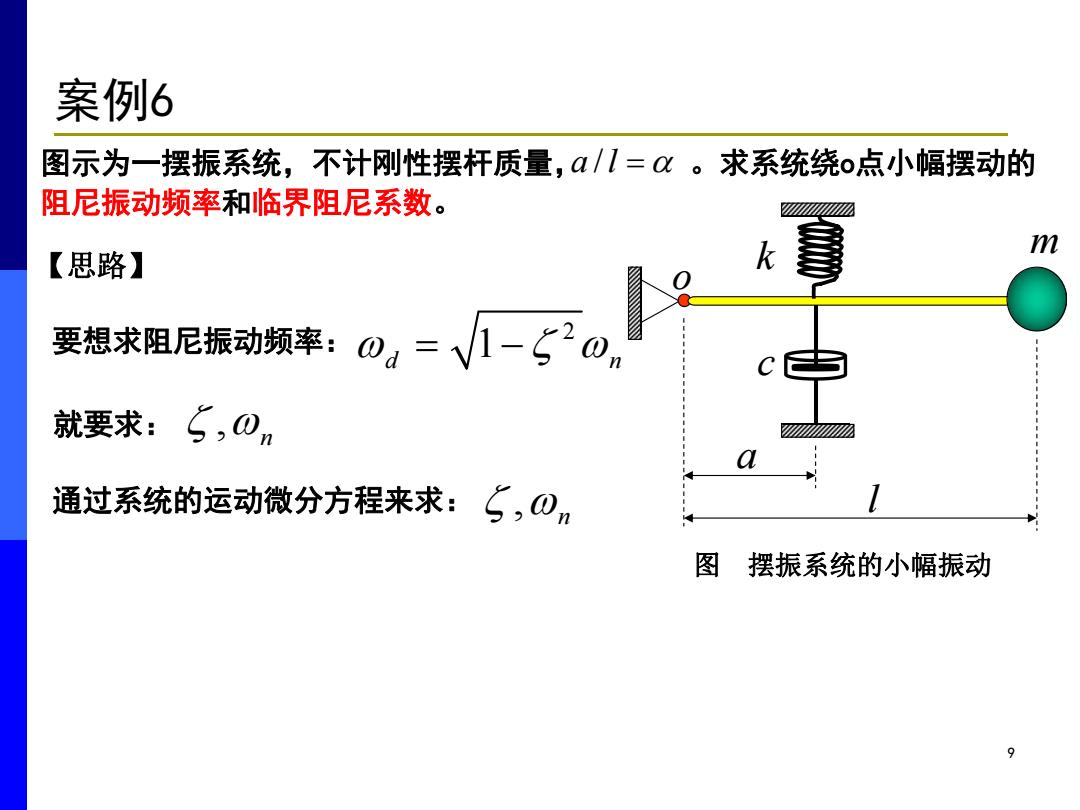
案例6 图示为一摆振系统,不计刚性摆杆质量,α/1=。求系统绕o点小幅摆动的 阻尼振动频率和临界阻尼系数。 【思路】 要想求阻尼振动频率:0,=√-专 就要求:5,0n 通过系统的运动微分方程来求:5,0m 图 摆振系统的小幅振动 9
9 图示为一摆振系统,不计刚性摆杆质量, 。求系统绕o点小幅摆动的 阻尼振动频率和临界阻尼系数。 c k m o a l a / l 图 摆振系统的小幅振动 【思路】 要想求阻尼振动频率: 2 1 d n 就要求: , n 通过系统的运动微分方程来求: , n 案例6

案例7 小球质量,刚杆质量不计,小球重量不计。写出(1)系统运动微分方程 ;(2)临界阻尼系数和有阻尼固有频率。 动力矩平衡建立系统运动微分方程 无阻尼固有频率: k m 阻尼比 5= 2.m.0m 有阻尼固有频率 04=0nV1-52 10
10 小球质量m,刚杆质量不计,小球重量不计。写出(1)系统运动微分方程 ;(2)临界阻尼系数和有阻尼固有频率。 θ 无阻尼固有频率: n k m 阻尼比 2. . n c m 2 1 d n 有阻尼固有频率 动力矩平衡建立系统运动微分方程 案例7
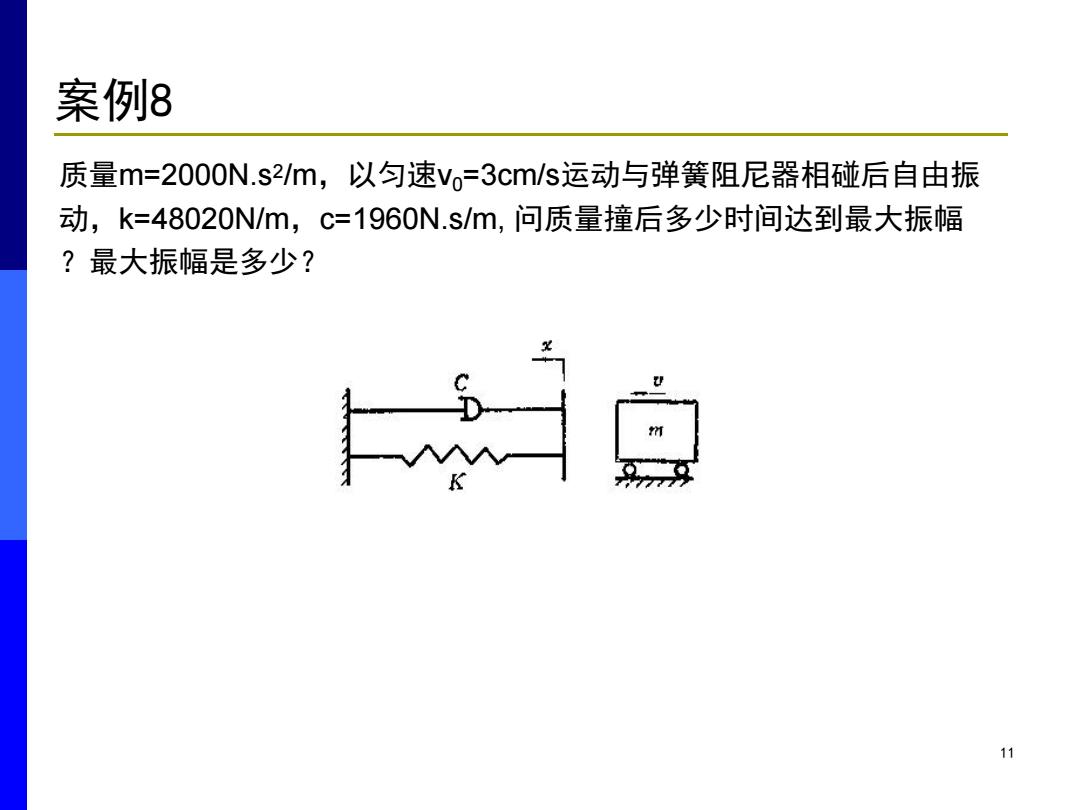
案例8 质量m=2000N.s2m,以匀速vo=3cm/s运动与弹簧阻尼器相碰后自由振 动,k=48020N/m,c=1960N.s/m,问质量撞后多少时间达到最大振幅 ?最大振幅是多少? 11
11 质量m=2000N.s2/m,以匀速v0=3cm/s运动与弹簧阻尼器相碰后自由振 动,k=48020N/m,c=1960N.s/m, 问质量撞后多少时间达到最大振幅 ?最大振幅是多少? 案例8