电子科技大学：《振动理论与声学原理 Vibration and Acoustics》课程教学资源（课件讲稿）第三章 单自由度系统受迫振动

3.1简谐力激励的强迫振动 m成+cx+x=Feo x= Bei(-)=Aei(o-0) k A= Fo 25s kV(1-s2)2+(25s)2 0(s)=arct B(S)= V1-s2)2+(25s)月 结论： (1) 线性系统对简谐激励的稳态响应是频率等同于激振频率， 而相位滞后激振力的简谐振动 (2)稳态响应的振幅及相位只取决于系统本身的物理性质 (m,k,c)和激振力的频率及幅值，而与系统进入运动的 方式（即初始条件）无关

11 i t mx cx kx F e     0   2 2 2 1 ( ) (1 ) (2 )      s s s 0 (  ) (  )      i t i t e Ae k F x 2 2 ( ) 1     s s arctg s 0 2 2 2 1 (1 ) (2 )    F A k s s 结论： 3.1简谐力激励的强迫振动

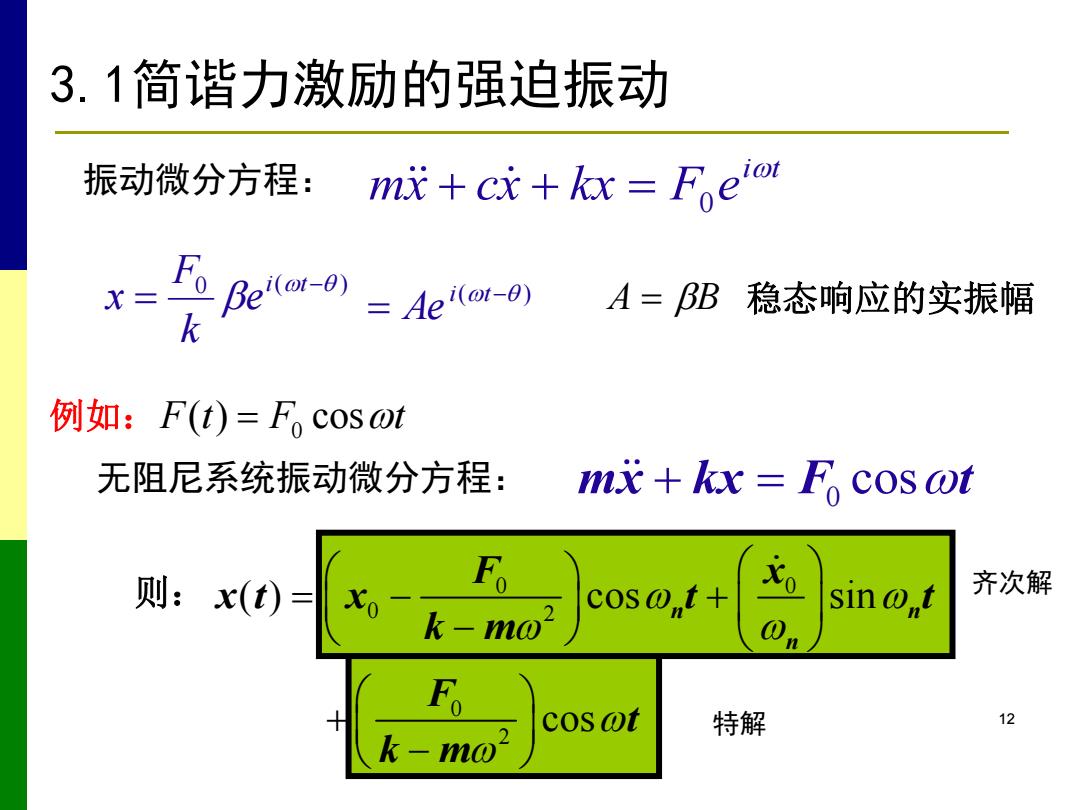
3.1简谐力激励的强迫振动 振动微分方程： n成+c+kx=F。eom X= Beia-0)=Ae-) A=BB稳态响应的实振幅 例如：F(t)=F,c0sot 无阻尼系统振动微分方程： m+kx=Fo cos @t 则：x(t) = Fo Xo cos@,t+ sin@,t 齐次解 k-mo F cos wt 特解 12 k-mo

特解 12 齐次解 i t mx cx kx F e     0   0 (  )    i t e k F x A  B 稳态响应的实振幅 F(t) F cost 例如：  0 0 0 0 2 0 2 ( ) cos sin cos n n n F x x t x t t k m F t k m                                则： (  )  i t Ae 3.1简谐力激励的强迫振动 振动微分方程： 0 无阻尼系统振动微分方程： mx  kx  F cost

则： x(= F cos@,t+ 氏 k-mo? sin@,t 齐次解 0 1 F cos wt 特解 13 k-mo 1.5 0.5 0 -0 -1.5 13 10 20 30 4050 60 70

13 特解 13 0 0 齐次解 0 2 0 2 ( ) cos sin cos n n n F x x t x t t k m F t k m                                则：

3.1简谐力激励的强迫振动 讨论：受简谐力作用的无阻尼系统 X=- Aei(or-0) 无阻尼情况（？=0)： 1 1 B(S)= V1-s2)2+(25s)2 1- 125s 0(s)=g =0 1-52 振幅 B iot x(t)= 1-s 14

14 i t e s B x t  2 1 ( )   i t e k s F  2 0 1 1  0 (  )    i t e k F x (  )  i t Ae 振幅 3.1简谐力激励的强迫振动 2 2 2 2 1 1 ( ) (1 ) (2 ) 1        s s s s 1 2 2 ( ) 0 1       s s tg s 讨论:受简谐力作用的无阻尼系统

3.1简谐力激励的强迫振动 振幅 无阻尼情况(G=0)：x()= B e 1-s2 0< 响应与外力方向 相同，幅值不同 Fo 1 1 B k1-s2 > 反相 n 共振 n 15

15 i t e s B x t  2 1 ( )  无阻尼情况（ζ＝0）：  i t e k s F  2 0 1 1  振幅 0 2 2 1 1 1 1 n F B k s            0 1 1 1 n n n           响应与外力方向 相同，幅值不同 反相 共振 3.1简谐力激励的强迫振动