
第八章白晶体结构的几何理论在第一章中我们已经介绍,晶体是具有格子构造的固体,其内部质点在三维空间都是呈周期性重复的规则排列的。每种晶体都有一定形式的内部结构。晶体结构及其化学组成,是决定晶体一切性质和现象的根本因素。与晶体外形上的晶面、晶棱之间一样,晶体结构内部的质点,相互间也都有一定的几何关系。不过,晶体结构是一种微观的无限图形,而晶体的几何外形则是属于宏观范畴的有限图形,两者之间存在着一个根本的差异,这就是:在晶体结构中必定有平移出现。实际上,晶体结构中质点的周期性重复排列,就是平移的一种表现:而空间格子的型式则体现了平移的组合关系。在本章中,我们首先将讨论如何来确定空间格子的型式,即空间格子的划分问题。不过,空间格子讨论的对象,只是纯粹几何意义上的一系列等同点,而在具体的晶体结构中,都是实在的质点。由此,相应地我们将引出晶胞的概念。至于质点间排列的对称关系,由于平移的出现,将导致产生新的对称要素,它们的组合构成了空间群。由空间群中的对称要素联系起来的一组相等的质点,则组成了等效点系。一个具体的晶体结构,即其中质点的具体排列形式,就可以由以上诸方面的几何特征来予以表征。晶体结构的具体形式,通常是在对晶体外部性质研究的基础上,根据晶体对X射线的衍射效应来测定的。其基本原理是,当X射线通过晶体时,由于结构中质点排列的方式和间距不同,产生的衍射线的方向就不同,质点的种类不同,所产生的衍射线的强度也不同。据此就有可能测定各个原子或离子的位置,从而也就确定了晶体的具体结构。但这一工作的过程,一般是较为繁复的,它属于X射线晶体学的范畴。从1929年使X射线通过晶体产生衍射效应的实验第一次获得成功以来,所有已知晶体结构的测定,基本上都是应用上述方法做出的。不过,由于近代科学技术的发展,现在已有可能利用高分辨率透射电子显微镜,来直接观察晶体的内部结构了。第一节十四种空间格子一、单位平行六面体的选择从第一章中我们已经知道,对应于每一个晶体结构,都可以抽象出一个相应的空间点阵,点阵中各个结点在空间分布的重复规律,便体现了具体晶体结构中质点105
105 第八章 晶体结构的几何理论 在第一章中我们已经介绍,晶体是具有格子构造的固体,其内部质点在三维空 间都是呈周期性重复的规则排列的。每种晶体都有一定形式的内部结构。晶体结构 及其化学组成,是决定晶体一切性质和现象的根本因素。 与晶体外形上的晶面、晶棱之间一样,晶体结构内部的质点,相互间也都有一 定的几何关系。不过,晶体结构是一种微观的无限图形,而晶体的几何外形则是属 于宏观范畴的有限图形,两者之间存在着一个根本的差异,这就是:在晶体结构中 必定有平移出现。实际上,晶体结构中质点的周期性重复排列,就是平移的一种表 现;而空间格子的型式则体现了平移的组合关系。在本章中,我们首先将讨论如何 来确定空间格子的型式,即空间格子的划分问题。不过,空间格子讨论的对象,只 是纯粹几何意义上的一系列等同点,而在具体的晶体结构中,都是实在的质点。由 此,相应地我们将引出晶胞的概念。至于质点间排列的对称关系,由于平移的出 现,将导致产生新的对称要素,它们的组合构成了空间群。由空间群中的对称要素 联系起来的一组相等的质点,则组成了等效点系。一个具体的晶体结构,即其中质 点的具体排列形式,就可以由以上诸方面的几何特征来予以表征。 晶体结构的具体形式,通常是在对晶体外部性质研究的基础上,根据晶体对 X 射线的衍射效应来测定的。其基本原理是,当 X 射线通过晶体时,由于结构中质点 排列的方式和间距不同,产生的衍射线的方向就不同,质点的种类不同,所产生的 衍射线的强度也不同。据此就有可能测定各个原子或离子的位置,从而也就确定了 晶体的具体结构。但这一工作的过程,一般是较为繁复的,它属于 X 射线晶体学的 范畴。从 1929 年使 X 射线通过晶体产生衍射效应的实验第一次获得成功以来,所 有已知晶体结构的测定,基本上都是应用上述方法做出的。不过,由于近代科学技 术的发展,现在已有可能利用高分辨率透射电子显微镜,来直接观察晶体的内部结 构了。 第一节 十四种空间格子 一、单位平行六面体的选择 从第一章中我们已经知道,对应于每一个晶体结构,都可以抽象出一个相应的 空间点阵,点阵中各个结点在空间分布的重复规律,便体现了具体晶体结构中质点

排列的重复规律。这种重复规律,可以由一系列不同方向的行列和面网来予以表征,并从而把整个空间点阵连接成格子状,构成空间格子。根据空间格子规律已知,由三组不共面的行列就可以决定一个空间格子。此时,整个空间格子将被划分成无数相互平行叠置的平行六面体。而上述三组相交行列便是这些平行六面体的棱。空间格子的组成要素包括:结点、行列、面网和单位平行六面体。单位平行六面体是空间格子的最小重复单位,整个晶体结构可以看成是单位平行六面体的堆砌。不难想象,对于同一个空间点阵,划分平行六面体的具体方式可以是各种各样的。就像一个平面点阵可以有无限多划分平行四边形的不同方式一样。在任何一种格子构造中,均可划分出无数不同形状和大小的平行六面体,从中选出一种能反映格子构造基本特征的作为代表,这就是单位平行六面体。选择单位平行六面体的原则(1)所选取的单位平行六面体应能反映格子构造中结点分布的固有对称性。(2)在满足(1)的前提下,棱与棱之间的直角最多。(3)在满足(1)、(2)的前提下,体积最小。图8-1(a)所示为一垂直于L4的面网上单位平行六面体一个面的选取。图中示出单位格子的六种不同选法。4、5、6三种选法中,在图形上没有L4,违反第一条原则:1、2、3三种选法中均有L4而且各棱相互垂直,符合(1)、(2)两条原则,但以1的体积最小,符合单位平行六面体选取的所有三条原则,可选作为单位平行六面体的一个面。图8-1(b)所示为一垂直L的面网上单位平行六面体一个面的选取,图中示出的7种选法也只有1所选取的图形才全部满足三个选取原则。2、5、6、7选取的图形虽然体积更小,但违反第二条选取原则,即棱与棱之间不垂直:4所选取的图形虽然满足(1)、(2)两条原则,但体积不是最小的,都不能作为单位平行六面体的一个面。对a和b另外两个面的选取亦做类似处理,即可得到其空间格子的单位平行六面体。婴ab图8-1在垂直于L4(a)和L(b)面网上单位平行六面体一个面的选取在空间格子中,按选择原则选择出来的平行六面体,即为单位平行六面体。它106
106 排列的重复规律。这种重复规律,可以由一系列不同方向的行列和面网来予以表 征,并从而把整个空间点阵连接成格子状,构成空间格子。根据空间格子规律已 知,由三组不共面的行列就可以决定一个空间格子。此时,整个空间格子将被划分 成无数相互平行叠置的平行六面体。而上述三组相交行列便是这些平行六面体的 棱。空间格子的组成要素包括:结点、行列、面网和单位平行六面体。单位平行六 面体是空间格子的最小重复单位,整个晶体结构可以看成是单位平行六面体的堆 砌。 不难想象,对于同一个空间点阵,划分平行六面体的具体方式可以是各种各样 的。就像一个平面点阵可以有无限多划分平行四边形的不同方式一样。在任何一种 格子构造中,均可划分出无数不同形状和大小的平行六面体,从中选出一种能反映 格子构造基本特征的作为代表,这就是单位平行六面体。 选择单位平行六面体的原则: ⑴ 所选取的单位平行六面体应能反映格子构造中结点分布的固有对称性。 ⑵ 在满足⑴的前提下,棱与棱之间的直角最多。 ⑶ 在满足⑴、⑵的前提下,体积最小。 图 8-1(a)所示为一垂直于 L 4 的面网上单位平行六面体一个面的选取。图中 示出单位格子的六种不同选法。4、5、6 三种选法中,在图形上没有 L 4,违反第一 条原则;1、2、3 三种选法中均有 L 4 而且各棱相互垂直,符合⑴、⑵两条原则,但 以 1 的体积最小,符合单位平行六面体选取的所有三条原则,可选作为单位平行六 面体的一个面。图 8-1(b)所示为一垂直 L 2 的面网上单位平行六面体一个面的选取, 图中示出的 7 种选法也只有 1 所选取的图形才全部满足三个选取原则。2、5、6、7 选取的图形虽然体积更小,但违反第二条选取原则,即棱与棱之间不垂直;4 所选 取的图形虽然满足⑴、⑵两条原则,但体积不是最小的,都不能作为单位平行六面 体的一个面。对 a 和 b 另外两个面的选取亦做类似处理,即可得到其空间格子的单 位平行六面体。 a b 图 8-1 在垂直于 L 4(a)和 L 2(b)面网上单位平行六面体一个面的选取 在空间格子中,按选择原则选择出来的平行六面体,即为单位平行六面体。它
的三条棱的长度以及棱之间的交角,是表征它本身形状、大小的一组参数,称为单位平行六面体参数。不同晶系的对称特点不同,单位平行六面体的形状也不同。对单位平行六面体的描述包括其形状、大小和结点的分布情况。选定了单位平行六面体,实际上也就选定了空间格子的坐标系。单位平行六面体的三根交棱便是三个坐标轴的方向。棱的交角α、β、也就是坐标轴之间的交角,棱长a、b、c是坐标系的轴单位。所以单位平行六面体参数也是表征空间格子中坐标系之性质的一组参数。实际上,从晶体外形上正确做出的晶体定向,应与晶体结构中的单位平行六面体对应一致。亦即三个结晶轴的方向应当就是单位平行六面体的三组棱的方向,晶体几何常数则应与单位平行六面体参数一致。其中轴角显然应当就是α、β、。轴率应当等于三根棱长之比,所不同的仅仅在于,单位平行六面体的三根棱长a、b、c是绝对长度,而轴率a:b:c只是相对的比值。二、各晶系单位平行六面体的形状和大小单位平行六面体的形状和大小,取决于三条棱的长度a、b、.c和棱之间的夹角α、β、,如图8-2所示。由于单位平行六面体的对称性必须符合整个空间格子的对称性,因此它必然与相应晶体图8-2单位平行六面体参数的图解结构及外形上的对称性相一致。对应于七个晶系,单位平行六面体的形状也有七种不同类型(图8-3):DGEF图8-3单位平行六面体的七种类型:A一立方格子:B一四方格子:C一正交格子:D一单斜格子:E一三斜格子:F一六方和三方格子:G一菱面体格子107
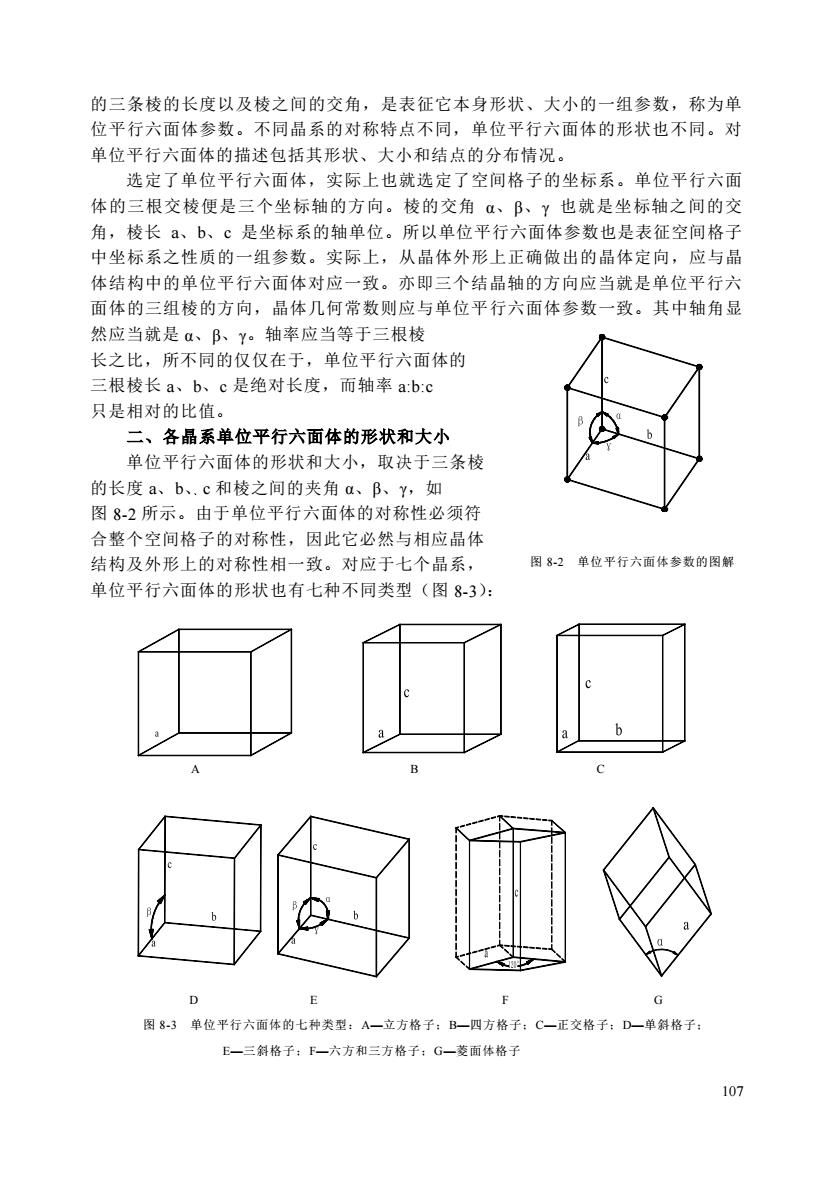
107 的三条棱的长度以及棱之间的交角,是表征它本身形状、大小的一组参数,称为单 位平行六面体参数。不同晶系的对称特点不同,单位平行六面体的形状也不同。对 单位平行六面体的描述包括其形状、大小和结点的分布情况。 选定了单位平行六面体,实际上也就选定了空间格子的坐标系。单位平行六面 体的三根交棱便是三个坐标轴的方向。棱的交角 α、β、γ 也就是坐标轴之间的交 角,棱长 a、b、c 是坐标系的轴单位。所以单位平行六面体参数也是表征空间格子 中坐标系之性质的一组参数。实际上,从晶体外形上正确做出的晶体定向,应与晶 体结构中的单位平行六面体对应一致。亦即三个结晶轴的方向应当就是单位平行六 面体的三组棱的方向,晶体几何常数则应与单位平行六面体参数一致。其中轴角显 然应当就是 α、β、γ。轴率应当等于三根棱 长之比,所不同的仅仅在于,单位平行六面体的 三根棱长 a、b、c 是绝对长度,而轴率 a:b:c 只是相对的比值。 二、各晶系单位平行六面体的形状和大小 单位平行六面体的形状和大小,取决于三条棱 的长度 a、b、c 和棱之间的夹角 α、β、γ,如 图 8-2 所示。由于单位平行六面体的对称性必须符 合整个空间格子的对称性,因此它必然与相应晶体 结构及外形上的对称性相一致。对应于七个晶系, 图 8-2 单位平行六面体参数的图解 单位平行六面体的形状也有七种不同类型(图 8-3): A B C D E F G 图 8-3 单位平行六面体的七种类型:A—立方格子;B—四方格子;C—正交格子;D—单斜格子; E—三斜格子;F—六方和三方格子;G—菱面体格子

1.等轴晶系,与之相对应的是立方格子,其单位平行六面体为立方体(图8-3A)。它的四条体对角线方向,就是等轴晶系所固有的4个L3的方向,立方体的三条交棱可以通过L3的作用相互重合。所以立方格子的单位平行六面体参数为a=b=c;α=β==90°2.四方晶系,与之相对应的是四方格子,单位平行六面体是一个横切面为正方形的四方柱体(图8-3B),柱面的交棱为c,它是四方晶系唯一的四次轴所在的方向,通过此四次轴的作用,必使a、b相互对称重复,但它们与c之间则无对称联系,所以其单位平行六面体参数为a=b+c;α==y=903.斜方晶系,与之相对应的为斜方格子,其单位平行六面体的形状如同一个火柴盒,三根互相垂直的交棱均不等长(图8-3C),单位平行六面体参数为ab±c:α===90°4.单斜晶系,与之相对应的是单斜格子,在单位平行六面体的三对面中,两对矩形平面之间成β角相交,且都垂直于另一对非矩形的面(图8-3D)。两对矩形平面的交棱规定为b,是单斜晶系唯一的二次轴方向,于是有a#b+c;α==90°,β>90°。5.三斜晶系,与之相对应的是三斜格子,其单位平行六面体是由三对不等边四边形构成的斜平行六面体(8-3E),因此有abc;α邦+90%6.六方晶系,对应的是六方格子。其单位平行六面体是一个底面呈菱形的柱体,底面上交棱间的夹角为60°和120°(图8-3F)。显然,在一个这样的平行六面体中不可能有六次轴存在,但是,如果把三个这样的平行六面体拼在一起,其底面便合成一个正六边形,就符合六方晶系的对称特点了。然而,这样拼成的六方柱体不再是平行六面体。作为单位平行六面体,仍是上述底面呈菱形的柱体,其柱面的交棱规定为C,它是六方晶系中唯一的六次轴方向。其单位平行六面体参数为a=b+c,α=β=90°,=120°7.三方晶系,对应于三方晶系的格子有两种,一种是三方格子,但形式上与上述六方格子完全相同,其单位平行六面体参数特征也与六方格子完全相同。三方晶系中的另外一种格子是菱面体格子,单位平行六面体相当于立方体沿L压扁或拉长所得,每一个面都呈菱形(图8-3G)此时L3只剩一个,与三方晶系的对称特点一致。三根交棱围绕L3成对称分布,因此有a=b=c;α=β=≠90°、60°、109°28'16"。在此,若α=β==90°、60°、109°28'16",则菱面体格子实际的对称性就要高于三方晶系,是属于立方格子的对称。此时根据单位平行六面体的选择原则,它们应当分别被改化为立方原始格子、立方面心格子和立方体心格子(图8-4)。三、单位平行六面体中的结点分布单位平行六面体中结点分布有四种情况,相对应有四种格子类型(图8-5)。1.原始格子(P):结点分布在平行六面体的八个角项。2.底心格子:结点分布在平行六面体的八个角项和一对平面的中心,又可细分为:108
108 ⒈ 等轴晶系,与之相对应的是立方格子 ,其单位平行六面体为立方体(图 8- 3A)。它的四条体对角线方向,就是等轴晶系所固有的 4 个 L 3 的方向,立方体的三 条交棱可以通过 L 3 的作用相互重合。所以立方格子的单位平行六面体参数为 a=b=c;α=β=γ=90°。 ⒉ 四方晶系,与之相对应的是四方格子,单位平行六面体是一个横切面为正 方形的四方柱体(图 8-3B),柱面的交棱为 c,它是四方晶系唯一的四次轴所在的 方向,通过此四次轴的作用,必使 a、b 相互对称重复,但它们与 c 之间则无对称 联系,所以其单位平行六面体参数为 a=b≠c;α=β=γ=90°。 ⒊ 斜方晶系,与之相对应的为斜方格子,其单位平行六面体的形状如同一个 火 柴 盒 , 三 根 互 相 垂 直 的 交 棱 均 不 等 长 ( 图 8-3C), 单 位 平 行 六 面 体 参 数 为 a≠b≠c;α=β=γ=90°。 ⒋ 单斜晶系,与之相对应的是单斜格子,在单位平行六面体的三对面中,两 对矩形平面之间成 β 角相交,且都垂直于另一对非矩形的面(图 8-3D)。两对矩形 平面的交棱规定为 b,是单斜晶系唯一的二次轴方向,于是有 a≠b≠c;α=γ=90°,β >90°。 ⒌ 三斜晶系,与之相对应的是三斜格子,其单位平行六面体是由三对不等边 四边形构成的斜平行六面体(8-3E),因此有 a≠b≠c;α≠β≠γ≠90°。 ⒍ 六方晶系,对应的是六方格子。其单位平行六面体是一个底面呈菱形的柱 体,底面上交棱间的夹角为 60°和 120°(图 8-3F)。显然,在一个这样的平行六面 体中不可能有六次轴存在,但是,如果把三个这样的平行六面体拼在一起,其底面 便合成一个正六边形,就符合六方晶系的对称特点了。然而,这样拼成的六方柱体 不再是平行六面体。作为单位平行六面体,仍是上述底面呈菱形的柱体,其柱面的 交棱规定为 c,它是六方晶系中唯一的六次轴方向。其单位平行六面体参数为 a=b≠c,α=β=90°,γ=120°。 ⒎ 三方晶系,对应于三方晶系的格子有两种,一种是三方格子,但形式上与 上述六方格子完全相同,其单位平行六面体参数特征也与六方格子完全相同。三方 晶系中的另外一种格子是菱面体格子,单位平行六面体相当于立方体沿 L 3 压扁或拉 长所得,每一个面都呈菱形(图 8-3G)此时 L 3 只剩一个,与三方晶系的对称特点 一 致 。 三 根 交 棱 围 绕 L 3 成 对 称 分 布 , 因 此 有 a=b=c ; α=β=γ≠90°、 60°、 109°28′16″。 在此,若 α=β=γ=90°、60°、109°28′16″,则菱面体格子实际的对称性就要高于 三方晶系,是属于立方格子的对称。此时根据单位平行六面体的选择原则,它们应 当分别被改化为立方原始格子、立方面心格子和立方体心格子(图 8-4)。 三、单位平行六面体中的结点分布 单位平行六面体中结点分布有四种情况,相对应有四种格子类型(图 8-5)。 ⒈原始格子(P):结点分布在平行六面体的八个角顶。 ⒉底心格子:结点分布在平行六面体的八个角顶和一对平面的中心,又可细分 为:

C心格子(C):结点分布在单位平行六面体的八个角项和平行(001)的一对平面的中心。A心格子(A):结点分布在单位平行六面体的八个角顶和平行(100)的一对平面的中心。B心格子(B):结点分布在单位平行六面体的八个角顶和平行(010)的一对面的中心。一般情况下,底心格子即C心格子。对A或B心格子,可以转换为C心格子时,应尽可能予以转换。仅在特殊情况下可直接使用A心或B心格子而无需转换。3.体心格子(I):结点分布在平行六面体的八个角顶和体心。4.面心格子(F):结点分布在单位平行六面体的八个角顶和每一个面的中心。b图8-4菱面体格子中α=90°,60°,109°28'16"时分别划分成a-立方原始格子,b-立方面心格子,c-和立方体心格子T山区区fdaD图8-5四种格子类型a-原始格子:b、c、d.-底心格子(b-C心格子:c-A心格子,d-B心格子):e-体心格子:f-面心格子四、十四种布拉维空间格子综合考虑平行六面体的形状和结点分布,空间格子共有14种。它最初是由布拉维推导出来的,故又称十四种布拉维空间格子(表8-1)。既然平行六面体有七种形状和四种结点分布方式,那么,空间格子为什么不是28种而是14种呢?这是因为某些格子类型是重复的;还有些格子类型与所在晶系的对称不符,因而不能出现在该晶系中。109
109 C 心格子(C):结点分布在单位平行六面体的八个角顶和平行(001)的一对 平面的中心。 A 心格子(A):结点分布在单位平行六面体的八个角顶和平行(100)的一对 平面的中心。 B 心格子(B):结点分布在单位平行六面体的八个角顶和平行(010)的一对 面的中心。 一般情况下,底心格子即 C 心格子。对 A 或 B 心格子,可以转换为 C 心格子 时,应尽可能予以转换。仅在特殊情况下可直接使用 A 心或 B 心格子而无需转换。 ⒊ 体心格子(I):结点分布在平行六面体的八个角顶和体心。 ⒋ 面心格子(F):结点分布在单位平行六面体的八个角顶和每一个面的中 心。 a b c 图 8-4 菱面体格子中 α=90°,60°,109°28′16″时分别划分成 a-立方原始格子, b-立方面心格子, c-和立方体心格子 a b c d e f 图 8-5 四种格子类型 a-原始格子;b、c、d.-底心格子(b-C 心格子;c-A 心格子,d-B 心格子);e-体心格子;f-面心格子 四、十四种布拉维空间格子 综合考虑平行六面体的形状和结点分布,空间格子共有 14 种。它最初是由布 拉维推导出来的,故又称十四种布拉维空间格子(表 8-1)。 既然平行六面体有七种形状和四种结点分布方式,那么,空间格子为什么不是 28 种而是 14 种呢?这是因为某些格子类型是重复的;还有些格子类型与所在晶系 的对称不符,因而不能出现在该晶系中