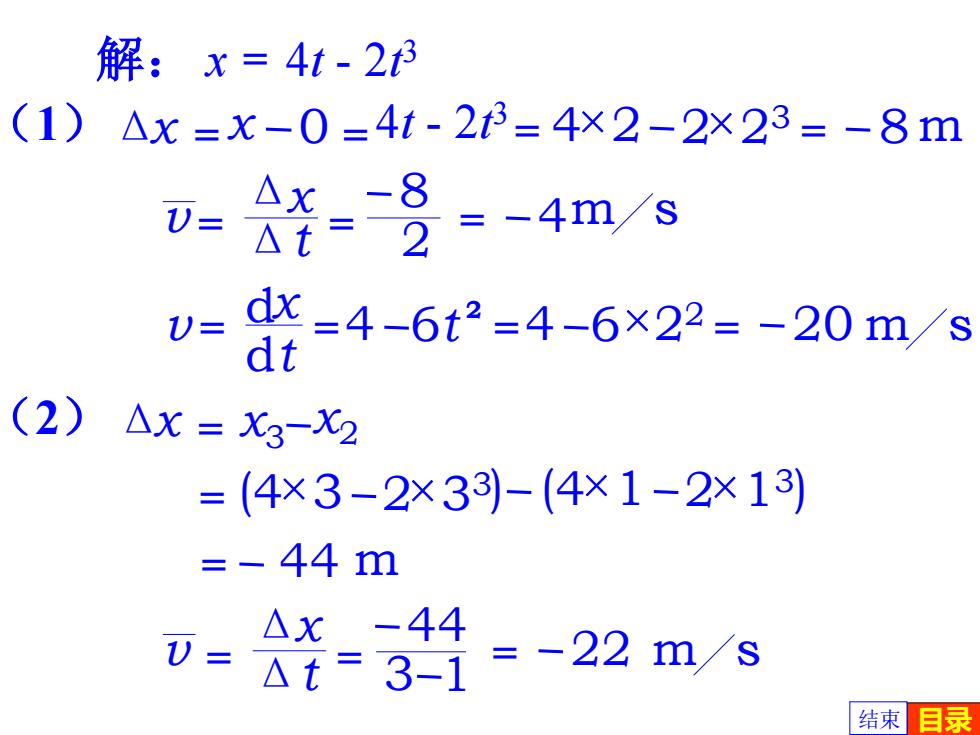
解:x=4t-23 (1)△x=x-0=4t-2t3=4×2-2X23=-8m V= △x_-8 =2 =-4m/s △t U= dx=4-6t2=4-6×22=-20m/S d (2) △X=X3-X2 =(4×3-2x33)-(4×1-2x13) =-44m △x-44 △t=3-1 =-22m/s 结束目录
x 0 解: x = 4t - 2t 3 (1)Δ =x 4t - 2t 3 = = 4×2 2×23 = 8 m t v = Δx Δ s = 8 2 = 4m 6 2 t v = dx = d 4 t 22 =4 6× = 20 m s = 4×3 2×33 4×1 2×13 ( ) ( ) = 44 m Δx = x3 (2) x2 t v = Δx Δ = s 44 3 = 22 m 1 结束 目录
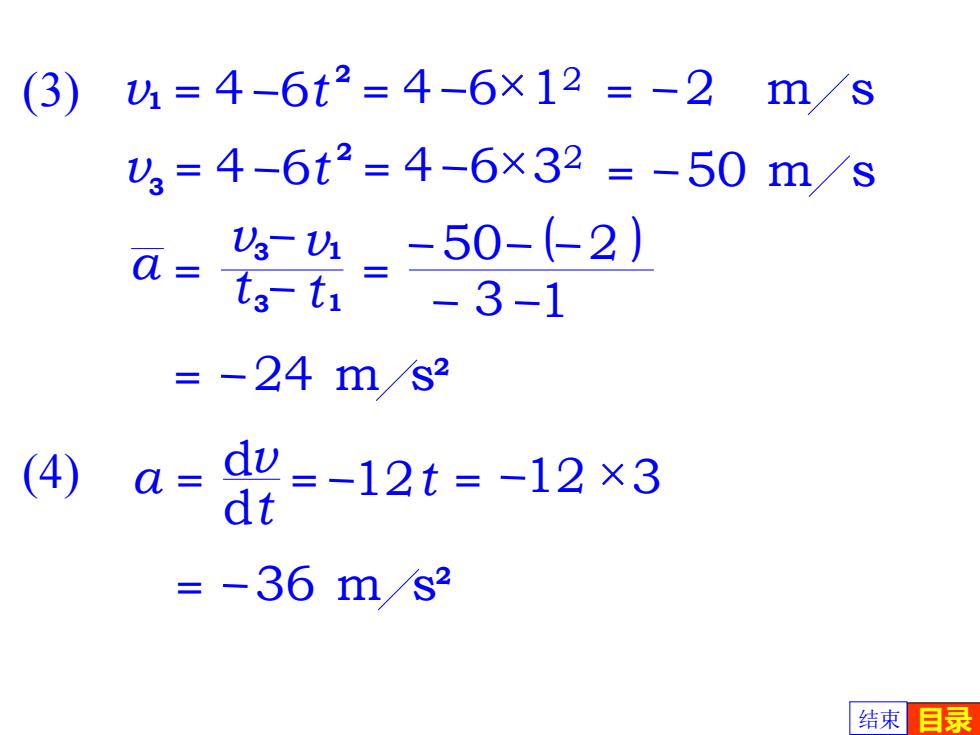
(3)4=4-6t2=4-6×12=-2 ms y3=4-6t2=4-6×32=-50ms %-y-50-(-2) a=ts-ti -3-1 =-24ms2 (4) a dv=-12t=-12×3 d =-36ms2 结束目录
3 6 2 v = 4 t = 4 6×32 = 50 m s 2 = 24 m s = 12 ×3 2 = 36 m s 1 6 2 v = 4 t = 4 6×12 (3) = 2 m s 12 t a = dv = d (4) t v1 ( ) v3 t 3 t 1 a = = 50 2 3 1 结束 目录

1-3一辆汽车沿笔直的公路行驶,速度 和时间的关系如图中折线OABCDEF所示。 (1)试说明图中OA、AB、BC、CD、 DE、EF等线段各表示什么运动? (2)根据图中的曲线与数据,求汽车在整 个行驶过程中所走的路程、位移和平均速度。 v/八m.s 10 10 2( 30 40 60 t/s -10 -10 结束目录
1-3 一辆汽车沿笔直的公路行驶,速度 和时间的关系如图中折线OABCDEF所示。 (1)试说明图中OA、AB、BC、CD、 DE、EF等线段各表示什么运动? (2)根据图中的曲线与数据,求汽车在整 个行驶过程中所走的路程、位移和平均速度。 10 20 30 40 50 60 -10 -10 -10 o t/s v/(m.s-1) 结束 目录

解:由v~t图的总面积可得到路程为: S=230+10x5+220x10 =200m) 总位移为 ax=230+10×5-320x10=0 所以平均速度也为零 结束目录
=200(m) 解:由v~t 图的总面积可得到路程为: 1 2 S = (30+10)×5 + 1 2 (20×10) 总位移为: Δx =0 1 2 = (30+10)×5 1 2 (20×10) 所以平均速度也为零 结束 目录

1-4.直线1与圆弧2分别表示两质点A、B 从同一地点出发,沿同一方向做直线运动的 wt图。己知B的初速o=bm/s,它的速率由 o变为0所化的时间为t1=2bs, (1)试求B在时刻t 的加速度; (2)设在B停止时, A恰好追上B,求A的速 b 度; (3)在什么时候, A、B的速度相同? 2b 结束目录
1-4.直线 1与圆弧 2分别表示两质点A、B 从同一地点出发,沿同一方向做直线运动的 v-t 图。已知B的初速v0 =b m/s,它的速率由 v0变为0所化的时间为t1= 2bs, (1)试求B在时刻 t 的加速度; (2)设在B停止时, A恰好追上B,求A的速 度; (3)在什么时候, A、B的速度相同? t v 2b b o 1 2 结束 目录