§6.1麦克斯韦方程 想象一个电容器与时变电压源相连 ∮,月i-Js=1 S2 矛盾 ∮,Aal=Jas=0 个i 上述矛盾导致麦克斯韦断言, 电容器中必须有电流存在, 由于电流不能由传导产生, 他将它称为位移电流 1认 (Displacement current)
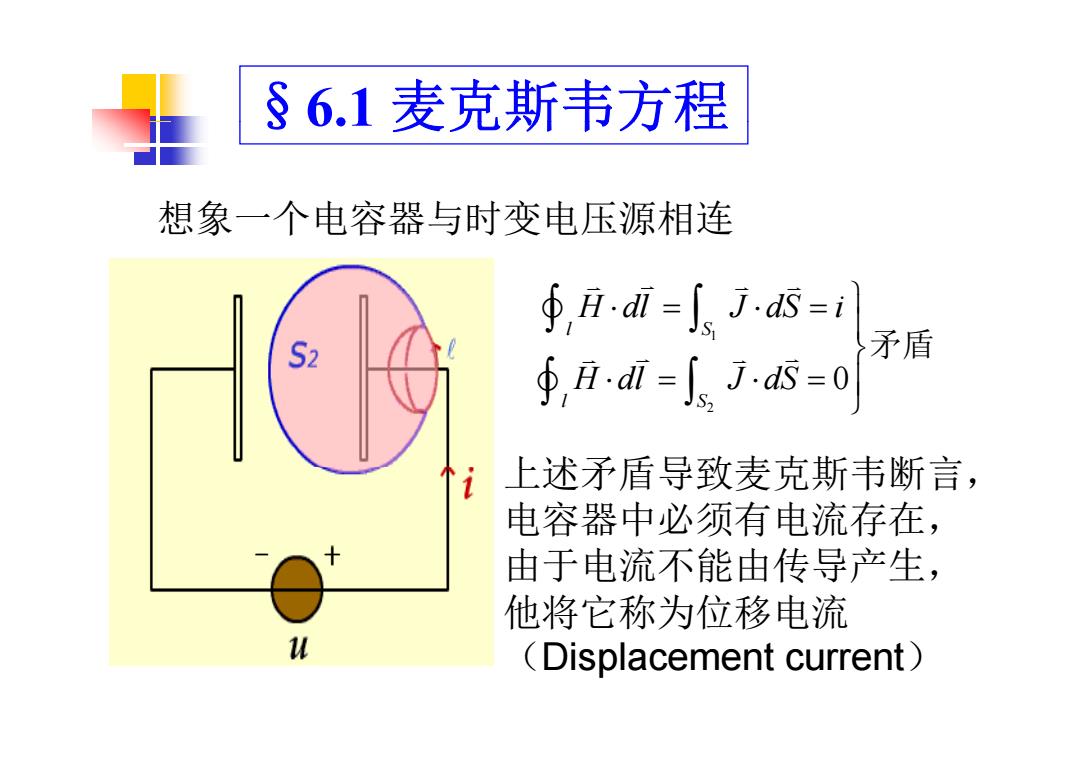
§6.1 麦克斯韦方程 想象 个电容器与时变电压源相连 dl dS 想象一个电容器与时变电压源相连 1 0 l S H dl J dS i H dl J dS 矛盾 2 0 l S H dl J dS 上述矛盾导致麦克斯韦断言, 电容器中必须有电流存在, 由于电流不能由传导产生, 他将它称为位移电流 (Displacement current)

§6.1麦克斯韦方程 高斯定理V·D=Pj 电荷守恒定律VJ= →j,=- →Vxi=j,+ aD D 定义 为位移电流密度(A/m2) 由于位移电流的存在使得不仅变化的磁场产生电场, 变化的电场也可以产生磁场,即随时间变化的电场 和磁场可以作为对方的漩涡源,这样即使在没有电 荷电流的区域,电磁场也可以再产生和传播
§6.1 麦克斯韦方程 D f 高斯定理 f J t 电荷守恒定律 0 f f D D J J t t 2 / f t t D A D H J m f 定义: 为位移电流密度( ) t t 由于位移电流的存在使得不仅变化的磁场产生电场, 变化的电场也可以产生磁场,即随时间变化的电场 和磁场可以作为对方的漩涡源,这样即使在没有电 荷电流的区域,电磁场也可以再产生和传播
§6.1麦克斯韦方程 例已知平板电容器的面积为S,相距为d, 介质的介电常数8,极板间电压为,u(t)。试求 位移电流1o:传导电流1,与0的关系是什么? 解:忽略极板的边缘效应和感应电场 电场 E=1,D=EE= &(t) d d ! 位移电流密度 JD= Ot d 位移电流 1以s- 0=C du 中传导电流 dt →位移电流
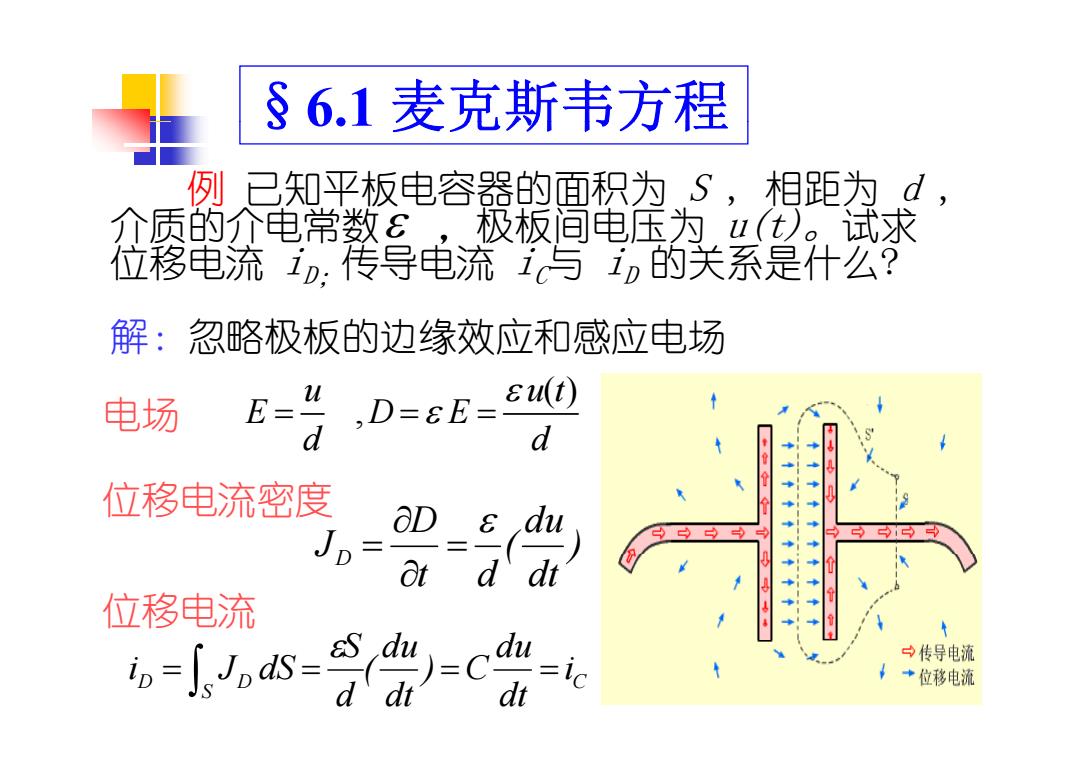
§6.1 麦克斯韦方程 例 已知平板电容器的面积为 S , 相距为 d , 介质的介电常数 ,极板间电 为压 u( )t 。试求 位移电流 iD;传导电流 iC与 iD 的关系是什么? ( )t 解:忽略极板的边缘效应和感应电场 , u u t E DE d d 电场 位移电流密度 ) du ( D JD 位移电流 ) dt ( t d JD S d d C S D D i dt du ) C dt du ( d S i J dS

§6.1麦克斯韦方程 由于磁力线永远是闭合的,所以静磁场的高斯定理 依然成立,只是磁感应强度为时变的而己。 所以可以得到麦克斯韦方程组: 又xi=J,+ aD 全电流定律 7×E= aB 电磁感应定律 8t ☑.B=0 磁通连续性原理 V.D=P 高斯定律
§6.1 麦克斯韦方程 由 于 磁 力 线 永 远 是 闭 合 的 , 所 以 静 磁 场 的 高 斯 定 理 B 由 于 磁 力 线 永 远 是 闭 合 的 所 以 静 磁 场 的 高 斯 定 依然成立,只是磁感应强度 为时变的而已。 所 以 可 以 得 到 麦 克 斯 韦 方 程 组 D H J 全 电 流 定 律 所 以 可 以 得 到 麦 克 斯 韦 方 程 组: H J f t B 全 电 流 定 律 0 B E t B 电磁感应定律 B 0 磁 通 连 续 性 原 理 D 磁 通 连 续 性 原 理 高斯定律

§6.1麦克斯韦方程 (D2-D)=P 边界条件 n×(E2-E,)=0 n(B2-B)=0 n×(i2-H)=J >麦克斯韦第一、二方程是独立方程,后面两个 方程可以从中推得。 >静态场和恒定场是时变场的两种特殊形式
§6.1 麦克斯韦方程 nD D ˆ ( ) 2 1 2 1 ( ) ˆ ( )0 sf nD D nE E 边界条件 2 1 2 1 ( )0 ˆ ( )0 nE E nB B 边界条件 2 1 ˆ ( ) sf nH H J 麦克斯韦第一、二方程是独立方程,后面两个 方程可以从中推得。 静态场和恒定场是时变场的两种特殊形式