
6.2.2无限大容量电源供电的三相短路电流分析 由电路的初始条件来确定 积分常数C,由换路定则知 ,电感中的电流不能突变 即在t0时,有 0)=i0) 短路后a相电流的完整表达式 i=lom sin(ot+a)+[I sin(a-p)-Isin(a-) 式中 U VR2+o'L2 =umf受) VR+R}+w2亿+L2 e=m光设)
6.2.2 无限大容量电源供电的三相短路电流分析 • 由电路的初始条件来确定 积分常数C,由换路定则知 ,电感中的电流不能突变 ,即在t=0时,有 2 1 2 2 2 R1 R2 L L U I m m 0 i(0 ) i t m m m i I t I I e sin sin sin 短路后a相电流的完整表达式 2 1 2 2 R1 L U I m m 1 1 1 tan R L 式中 1 2 1 1 2 tan R R L L
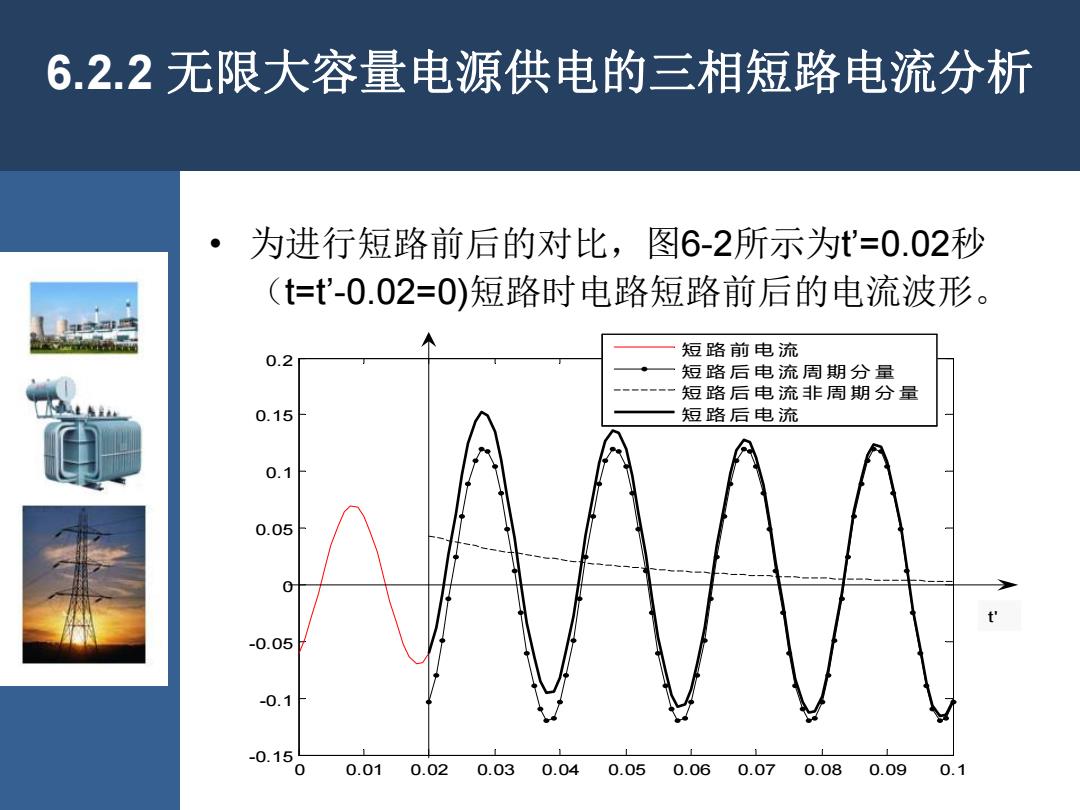
6.2.2无限大容量电源供电的三相短路电流分析 。为进行短路前后的对比,图6-2所示为t'=0.02秒 (t=t'-0.02=0)短路时电路短路前后的电流波形。 短路前电流 0.2 短路后电流周期分量 短路后电流非周期分量 0.15 短路后电流 0.1 0.05 0 -0.05 -0.1 -0.15 0 0.010.020.030.040.050.060.070.080.090.1
• 为进行短路前后的对比,图6-2所示为t’=0.02秒 (t=t’-0.02=0)短路时电路短路前后的电流波形。 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 -0.15 -0.1 -0.05 0 0.05 0.1 0.15 0.2 短 路 前 电 流 短 路 后 电 流 周 期 分 量 短 路 后 电 流 非 周 期 分 量 短 路 后 电 流 t' 6.2.2 无限大容量电源供电的三相短路电流分析

6.2.2无限大容量电源供电的三相短路电流分析 ·短路电流各分量之间的关系可以用相量图来表示。 纵轴 短路电流非周期 分量初值的大小 与短路发生的时 合闸角 刻有关,也就是 横轴 说与合闸角α有 关。 io 1 ①m
• 短路电流各分量之间的关系可以用相量图来表示。 6.2.2 无限大容量电源供电的三相短路电流分析 合闸角 短路电流非周期 分量初值的大小 与短路发生的时 刻有关,也就是 说与合闸角 有 关。

6.2.2无限大容量电源供电的三相短路电流分析 根据三相对称电路的特点,还可以写出短路 后b、c两相电流的表达式 虽然它们的电路参数是相同的,但它们的合 闸角分别为a-120°和4+120°,可见非周期 分量为最大值或零值的情况只可能在一相出 现
• 根据三相对称电路的特点,还可以写出短路 后b、c两相电流的表达式 。 • 虽然它们的电路参数是相同的,但它们的合 闸角分别为 和 ,可见非周期 分量为最大值或零值的情况只可能在一相出 现。 6.2.2 无限大容量电源供电的三相短路电流分析 o 120 o 120

例6-1 已知图6-1所示电路中,已知三相对称电源 的4,=10W2sin2,z50kV,R1=R2=10, L1=L2=10mH,则: 0 1)设t=0时短路(即在a相电压瞬时值为零 时短路) ·2)设t=0.005s时短路, ·3)设t=0.01s时短路, 求各相的合闸相角,短路后电流的周期分 量有效值,各相的非周期分量初值,时间 常数
例6-1 • 已知图6-1所示电路中,已知三相对称电源 的 ,R1=R2=10, L1=L2=10mH,则: • 1)设t=0时短路(即在a相电压瞬时值为零 时短路) • 2)设t=0.005s时短路, • 3)设t=0.01s时短路, • 求各相的合闸相角,短路后电流的周期分 量有效值,各相的非周期分量初值,时间 常数。 ua 10 2 sin2 50tkV