
7 以象标准反应烙那样定义: △Fn=∑M,AfIw-∑MA/ial (1-6) S-P jR 其中4仍:是标准的生成自由能,某些物质的标准生成自由能列于表1~4中,对于任意温度、 任意压力下的自由能可可由下式计算, (1-7) 于是对于任意温度、任意压力下的反应自由能为, FA,EMa, 当△F=0时,便达到化学平衡状态。 表1-4生成的自由能4 气 气者有机化合物 (CH. -12.14 -22.7 -12.72 n-T(C.Hi) -4.30 -68.52 (C: 新良烧(CH) 3.60 18:28 1丁塘(CH 397 m-2-丁烯(CH) 1 及-2-T 15.05 氧甲接(CH:C1) -14.00 气 48.58 甲(CH,OH) -39,78 乙尊(C:H,OHD -41.77 19.0 酸(C:H,O) 98. 苯(C,Hy 31.00 三氧甲规(CH,C1:) -17.10 54.3 因氯化费(CC1,》 -1.40 §1.4质量作用定律及可逆反应的平衡常数 质量作用定律是描写反应速率与反应物质的浓度之间的相互关系。1867年Gm1berg和 Wag心首先给出了这一关系。设化学反应的一般式为加 V:A,+YA+…i+A:+…

8 或 B%i,‘Ev4: (1-8) 其中¥,和称为化学计算系数。则质量作用定律可表示成: w=kCiC…=kC 其中为反应速率常数。 一殷说来,所有的反应都是可逆反应,因此式(1-8》可写成 EvAEvidi 正反应速率为: 知:=kΠc 逆反应速率为: m:='Πc 当达到化学平衡时: kΠc=k'Πci 即 Πc 1-9》 其中点称为平衡常数。最的下标“C”表示它是以浓度定义的平衡常数。 §1.5平衡常数和标准反应自由能的关系 若以下列反应式 aA+BcC+dD 为例,则在标准状态下转变成的生成物,根据式(1-6)其标准反应自由能是, AF:=cAfic+daf)n-adf).-bafh 在任意给定的压力下的反应自由能为: △F:=cfe+dAf,-a△f.-bAf: 这样,由于压力变化引起的反应自由能的变化为: AF9-AF5=c(△/ie-Afi.)+d(a。-ai.)-a(af7-△Ji.) -6(af.-fi) 将方程式(1-7)代入上式得: AF-AF;=RT(c In Pe+dIn Pa-aln P-bln P) -RT lo ip 当平衡时△F:=0,这样得:

9 器)船 (1-10) 令 器 其中k,为平衡常数。k的下标“p”表示按分压定义的平衡常数。将质,代入式(任-10)得, 政 =(g) (1-11) ,式(1-11)建文了平衡常数与标准反应自由能的关系,其中△F是一个常数,因此在给定的 温度下,,是一个常数。表1-5中列出了十七种气相反应的,值。这十七种气相反应的顺 序如下: 1.S02+20,一S0, 10.C01+H,=C0+H,0 2.20+2一N0 11.C0+C=2C0 12.c0,c0+20 4。H,一H 13.2C+H,≠C,H, 5,+=NB 14.H,+C0一CH, 6.2一N 15.C+2H,=CH, 7.N0=aN+0 16.C0+2H=CH,0H 8。,0一4,+20: 17.C0+3H,-CH,+H,0 9.H,0=一H,+0H k。和,的关系如下: c=些 这样 k= (1-12) 其中△M,为反应过程中气体摩尔数的变化量,即: w三0名=0+)-a+) 如果一个反应在反应过程中摩尔数不发生变化,则,二k。如H,+之,一出的反应就 是这种例子
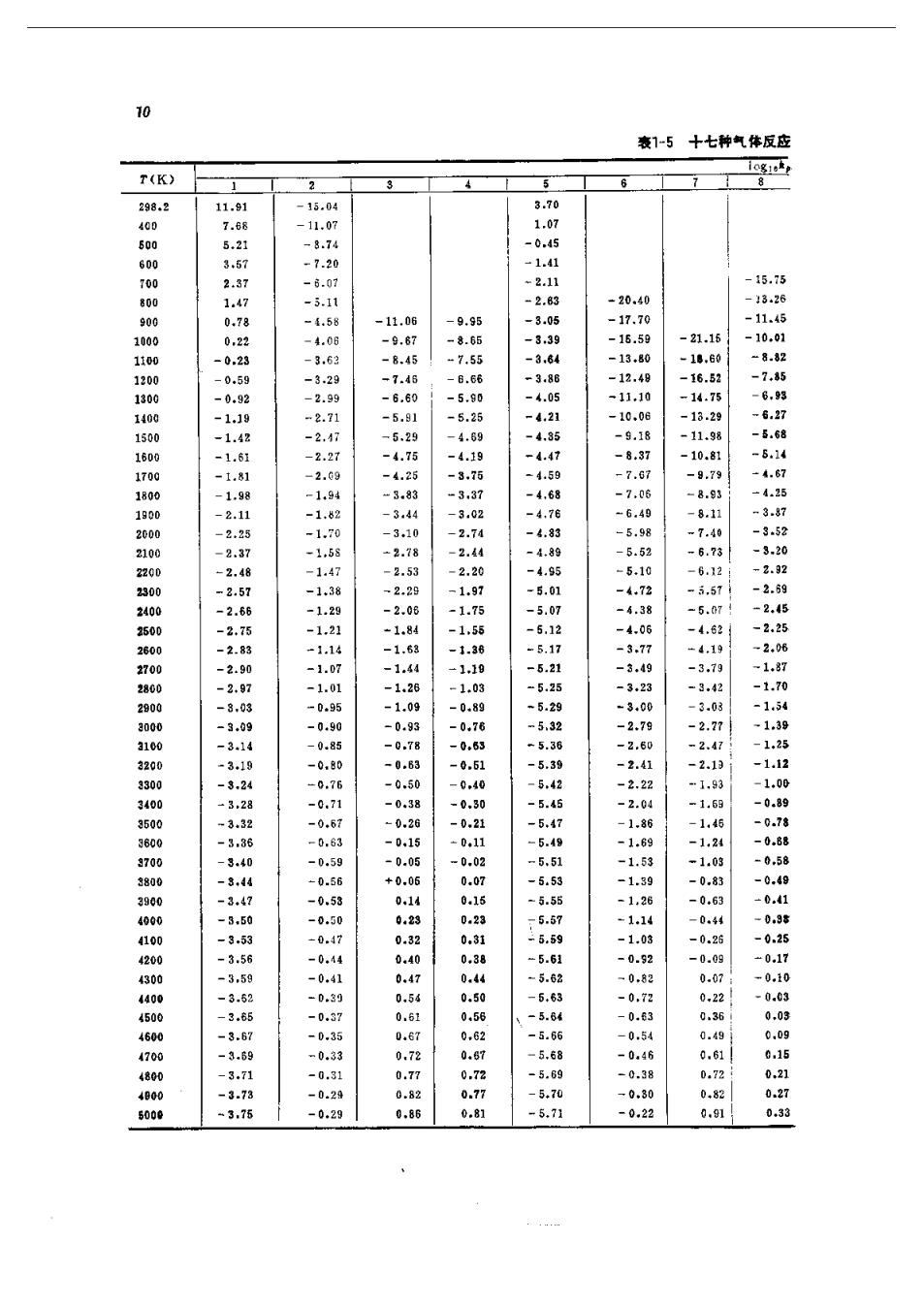
表1-5十七种气体反 T(K) 飞1幼101114中11111111项项1亿011141414441
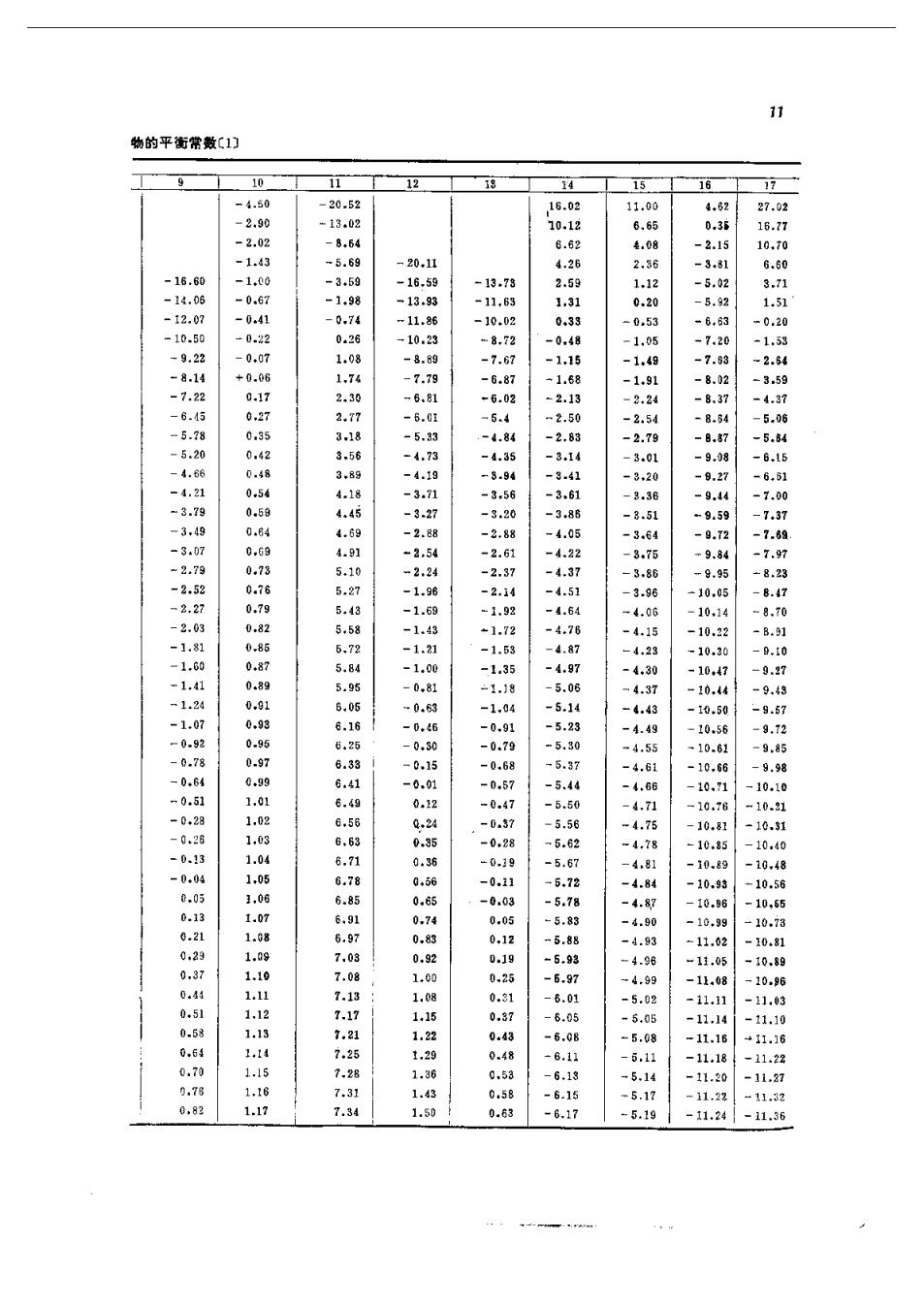
物的平衡常数C1门 16 111体1111110141佛40114中诚41亿441444414111111412