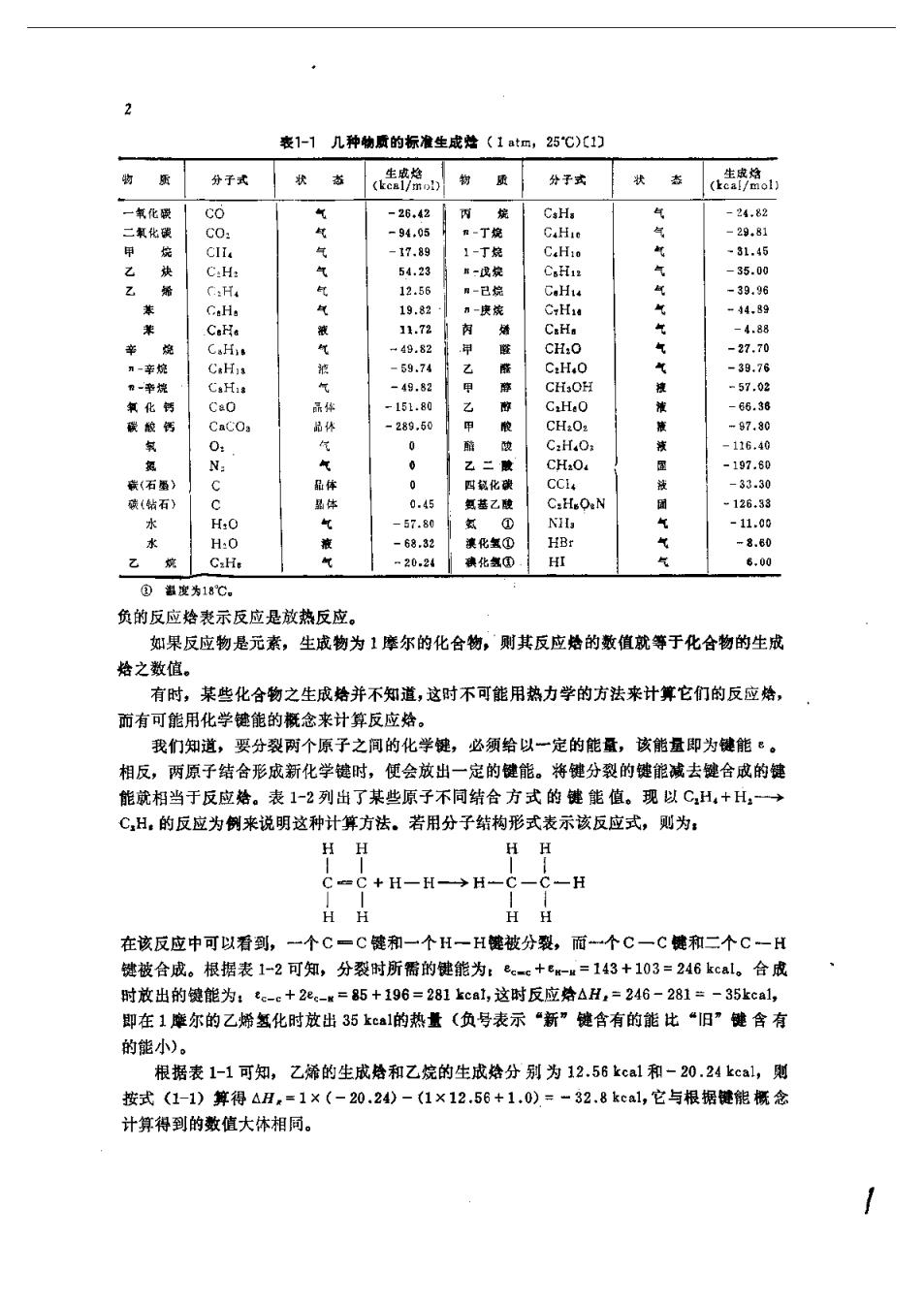
表1-1几种物质的标准生成址〈1at四,25℃)(1) 分于式 状 状志《告格o: 一氧化 CO 26.42 4,8 94.0 C:H 12.5 气气气气气气气淮液液团团气 -39.96 9.8 -27.70 -39.78 9.8 0. C2H.0 16.40 0 CHaO. 197.89 石 C.H.ON 1265 水 H0 5.80 -11.09 H:0 气 -68.32 澳化氢① HB: -8.80 C:H 2024化氢 HI ,00 ⑧温堂为18心 负的反应老示反应是放热反应。 如果反应物是元素,生成物为1座尔的化合物,则其反应处的数值就等于化合物的生成 焙之数值。 有时,某些化合物之生成婚并不知道,这时不可能用热力学的方法来计算它们的反应 而有可能用化学键能的概念来计算反应给。 我们知道,要分裂两个原子之间的化学键,必须给以一定的能量,该能量即为健能·。 相反,两原子结合形成新化学时,便会放出一定的健能。将键分裂的键能减去健合成的 能就相当于反应给。表1-2列出了某些原子不同结合方式的键能值。现以CH,+H,一→ ℃H。的反应为例来说明这种计算方法。若用分子结构形式表示该反应式,则为: H C+H一H→片 一H HH HH 在该反应中可以看到,一个C一C键和一个H一H被分裂,而个C一C能和二个C一H 被合成。根据表1-2可知,分裂时所需的能为: w=143+103=246kcal。合成 时放出的能为:e-e+2-=85+196=281kca1,这时反应给△H,=246-281=- 35kcal, 即在1摩尔的乙婚氢化时放出35ka1的热量(负号表示“新”健含有的能比“旧”健含有 的能小)。 根据表1-1可知,乙烯的生成烙和乙烷的生成给分别为12.56kca1和-20.24kca1,则 按式(1-1)算得△H,=1×(-20.24)-(1×12.56+1.0)=-32.8kca1,它与根据链能概念 计算得到的数值大体相同

委1-2望能(kc1/饿)C1们 量 健 能 量 能 C-B: 6 H一B c- C-N N C--CI 8 H-H 80 再举一例: 甲烷直接氧化生成二氧化碳和水蒸汽的反应烙的计算。其化学结构式为 H H+0-0+00 0-C一0+H -0- -H+H-O一H 由上式可以看出有四个C一H键被分裂;二个C一0健和四个0一H赞被合成。分裂四个 C一H键和二个0-0键所清的能量为:(4×98+2×33)=458kcl。而形成二个C一0能 和四个0一H键释放的能量为:(2×86+4×109)=608kcl,因此△H,=458-608= -150kca,即甲烷的氧化反应其反应烙约为-150kcl, 虽然用健能来计算反应焙是较粗赖的,但在没有化合物的生成给资料的情况下,采用使 能的概念来计算反应络是很有用的。 前而讲的反应给都是指的反应给的标准值,即是在压力为1标准物理大气压,温度为 25℃时确定的。那么对任意给定的压力和温度下的反应结应如何计算呢?我们知道,对于理 想气体来说,热与压力无关,但与温度有关,现以最简单的反应来说明反应处与温度的关 系。设反应物R有:个摩尔,经化学反应后变成P个摩尔的生成物P,即:R→P,反应 给应等于R变到P过程中系统的烙的减少,即,: △H:=△H,-△H.ePah,-rAa. △H:随盗度的变化为: (1-2) 由定压比热的定义得, a-vem (1-3) 这就是说反应给随温度的变化率等于定压下反应物和生成物的比热差,这个关系膏之为蕃尔 荷夫(Kirchof)定律。积分式(1-3)得 △H-pc-rC,)dr+Him 「T (1-4) 其中AHa,可根据生成给算得。C、C:随温度的变化可查有关物性表,这样可由式(1 4)计算任意温度下的反应给

g 若C,和C与温度无关,则: AH=(PC-rC)(T -298)+ (1-5) Kirehoff定律可以进一步推广到反应物和生成物多于一种的反应系统中去,若反应为: A+B+C+M+N+O+… 这时只要将比热取为平均值即可,即: C=xCa+xC+…=∑x,C C=x.Cp+×,C+…=∑xC 其中、x,(S=A、B、C,K=M、N、O…)分别为第S种和K种成分的摩尔相对 浓度。 例:计算水在90℃时的反应。假定初始的混合物是按化学当量混合的。且C=a+ b7,对H来说4=6.94,6=-0.2×10对0,*说a=6.09,6=3.25×10。 解:由表1-1知,在标准情况下水的反应烙为68.32k©al/mol。初始混合物为:H,+ 0,因货:-昌最终混合物为H0,所以1。于是:方员,号 C=号(6.94-0.2×10T)+(6.09+3.25×10-T) =6.G4-0.00024Tcal/(mol.K) C=C18 cal/(mol.K) pC-rC=18-26.64-0.00024T)=8.04+0.00036T 代入式(1-4)得: △H=-67,782kea1 反应给还与其物理状态有关。例如氧与氢反应生成水,生成的水可以是汽态,也可以是 液态,这取决于温度。表1-1列出了液态水和汽态水的生成给值。表1-1中的其他各项也指 出了△,值与产物的状态有关。表1-3表明燃料的燃烧热△h。也和它的状态有关。例如: H2+0,-→H:(液态),△,=-68.31kca1 如果产生的水是蒸汽状态,我们必须将蒸发给加到H,0(液)的生成.上去,即: H,0(液)→H,0(汽),6an=10.52kca1 根据盏斯定律(见下节)有: ,+20,一→H,0(,44,=-57.79kal 11.8烧热(然烧给)
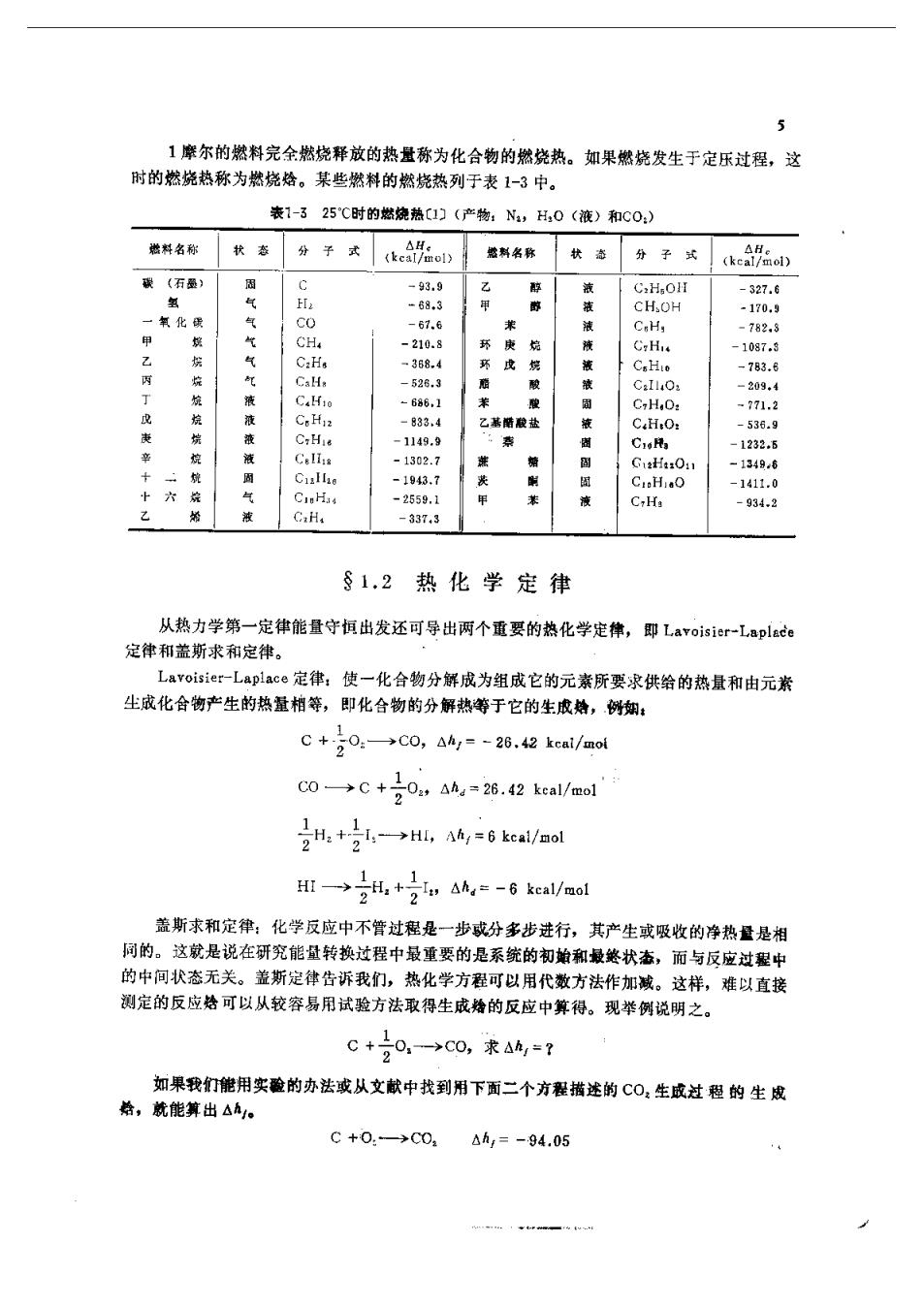
5 1摩尔的燃料完余燃烧释放的热量称为化合物的燃烧热。如果燃烧发生于定乐过程,这 时的燃烧热称为燃烧格。某些燃料的燃烧热列于表1-3中。 表1-325℃时的燃烧热C1)(产物:N,0(液)和C0: 名称秋老分子式合料名路款分子e。 -327.6 氧化安 c -170. 气气 CH =210. C.H. 10 368. CH 783.6 C.H. 209 C.H -833. c,H.0 1149.9 CaRa 1232 10 -2559.1 C.H. C.H -337,3 §1.2热化学定律 从热力学第一定律能量守恒出发还可导出两个重要的热化学定律,即Lavoisier--Laplade 定律和盖斯求和定律。 Laroisier一Laplace定律:使一化合物分解成为组成它的元素所要求供给的热量和由元素 生成化合物产生的热量柏等,即化合物的分解热等于它的生成蜂,例蜘: C+号0:→C0,△4g=-26.42kcai/aol C0→C+号0,Ana=26.42kcal/mol 一→,+2,AA,=-6 keal/mol 盖斯求和定律:化学反应中不管过程是一步成分多步进行,其产生或吸收的净热量是相 同的。这就是说在研究能量转换过程中最重要的是系统的初蜘和最终状杰,而与反应过程中 的中间状态无关。盖斯定律告诉我们,热化学方程可以用代数方法作加减。这样,难以直接 测定的反应烙可以从较容易用试验方法取得生成婚的反应中算得。现举例说明之。 C+20,-→C0,求Ah,=? 如果我们能用实酸的办法或从文献中找到用下面二个方程描述的C0:生成过程的生成 给,就能算出△五。 C+0.-→C0.△h,=-94.05 y-

6 c0+20,一00: △H,=-67,62 两式相碱得, C+0.-c0-20→c0,-C0-94,05+7.62 即 c+20,→c0-26.43 △h1=-26:43 盖斯定律的另一个用处就是根据已知的各反应物和生成物的燃烧给来求出反应络。例 如 C,H+H→C,H,求△H=? 从表1-3中查得乙桶、氢和乙烷的燃烧热在标准温度下分别为-337.3、-68.3和-368.4kcl, 写出下列三个燃烧方 CH,+30,-→2C02+2H,0,k,=-337.3kca .>H,Ah=-68.3 keal CH+20,→2C0+3H,0,A4,=-383.4kca 若用头二个方程的和减去第三个方程,则得: CaH,+H:>CH,=-37.2 keal §1.3热力学平衡与自由能,化学平衡与反应自由能 热力学平衡意味着系统的各参数保持恒定并均匀分布,判别热力学系统是否能达到平衡 状态,可由热力学第二定律米描写。由热力学第一定俸知, dg=de+pdo 对于不可逆过程,则根据热力学第二定律有: s>兽 Tds>de+pdo de +pdo-Tds<0 对于定压、定温过程,上式可改写成: d (e+po-TS)n<0 d(h -TS).< f=A-TS-一吉布斯(Gbbs)自由能 (d<0 因此等温等压过程总是向自由能减小的方向进行。当过程达到平衡状态时,则自由能为最小, 这时(d,=0,因而在等温等压下热力学平衡的条件可以写成(d…=0。这个判捌式 可以推广到化学平衡中去,这时必须定义一个“反应自由能”。对于标准反应自由能的定义可