
第一章气体的PVT关系 §1.1理想气体的状态方程 §1.2理想气体混合物 §1.3气体的液化及临界参数 §1.5对应状态原理及普遍化压缩因子图 4上一内容 下一内容 ◇回主目录 与返回 2024/9/5
上一内容 下一内容 回主目录 返回 2024/9/5 第一章 气体的PVT关系 §1.1 理想气体的状态方程 §1.2 理想气体混合物 §1.3 气体的液化及临界参数 §1.5 对应状态原理及普遍化压缩因子图

§1.1理想气体的状态方程 1.理想气体的状态方程 pV=nRT R=PV nT [R]= Pa:m=Pa.m.mol.K mol.K J.mol-1.K-1 {R}=8.315 上一内容 下一内容 ◇回主目录 与返回 2024/9/5
上一内容 下一内容 回主目录 返回 2024/9/5 §1.1 理想气体的状态方程 pV=nRT {R}= 8.315 1.理想气体的状态方程 nT pV R = 1 1 3 1 1 3 J mol K Pa m mol K mol K Pa m [ ] − − − − = = R =

§1.1理想气体的状态方程 1.理想气体的状态方程 也可以写为pVm=RT 因为Vm=Vn 或 pV=RT M 上一内容 下一内容 ◇回主目录 与返回 2024/9/5
上一内容 下一内容 回主目录 返回 2024/9/5 §1.1 理想气体的状态方程 1.理想气体的状态方程 也可以写为 pVm=RT 因为 Vm=V/n RT M m 或 pV =

§1.1理想气体的状态方程 例:计算25℃,101325Pa时空气的密度。 (空气的分子量为29) 解: 101325 8.315×(273.15+25) mol.m-3 =40.87molm-3 -M-40s7×29ygm3=1.185kg:m3 上一内容 下一内容 ◇回主目录 与返回 2024/9/5
上一内容 下一内容 回主目录 返回 2024/9/5 §1.1 理想气体的状态方程 例:计算25℃,101325Pa时空气的密度。 (空气的分子量为29) 解: ( ) 3 3 4 0.8 7 mol m mol m 8.315 273.1 5 2 5 101325 − − = + = = RT p V n 3 3 4 0.8 7 2 9 g m 1.185 k g m − − M = = V n d 空 气=
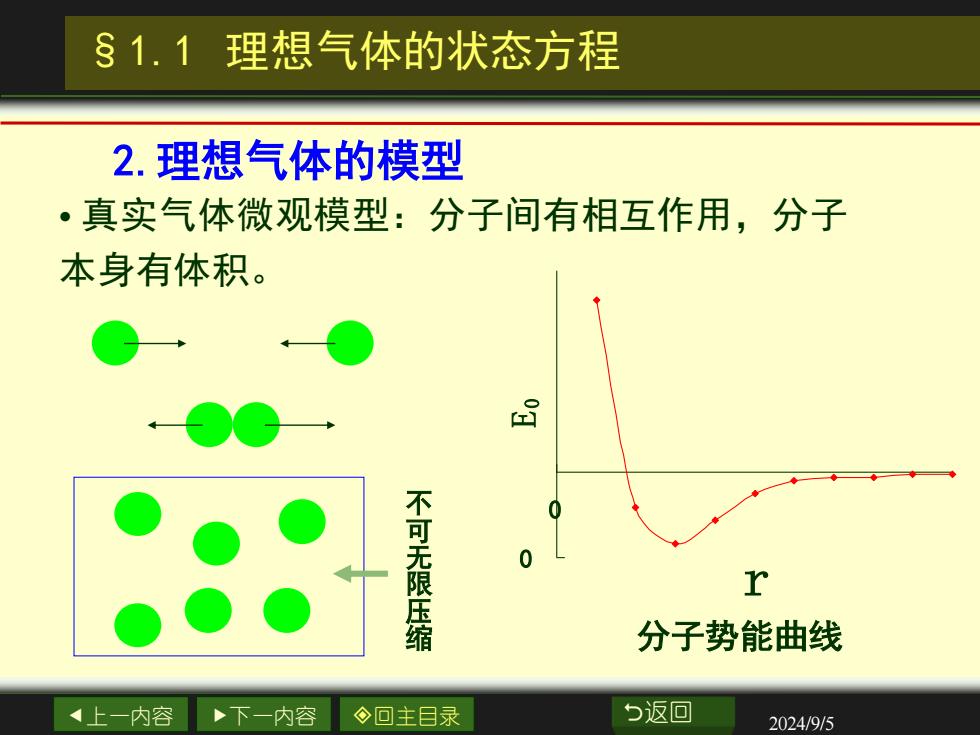
§1.1理想气体的状态方程 2.理想气体的模型 ·真实气体微观模型:分子间有相互作用,分子 本身有体积。 品 0 不可无限压缩 r 分子势能曲线 4上一内容 下一内容 ◇回主目录 与返回 2024/9/5
上一内容 下一内容 回主目录 返回 2024/9/5 • 真实气体微观模型:分子间有相互作用,分子 本身有体积。 §1.1 理想气体的状态方程 2.理想气体的模型 不 可 无 限 压 缩 分子势能曲线 0 0 r E0