《化工热力学》课程教学课件（PPT讲稿）第三章 流体的热力学性质

四大微分方程式是将热一律和热二律与这些性 质的定义式相结合推导出来的。 如（3-1)式： 由热一律知：dU=δQ-δW=δQ-PdV 由热二律知：δQ=TdS 由上述二式推出：dU=TdS-PdV 式(3-2)：由H=U+PV知： dH-dU+d(PV) =dU+VdP+PdV -TdS-PdV+VdP+PdV =TdS+VdP

四大微分方程式是将热一律和热二律与这些性 质的定义式相结合推导出来的。 如（3-1）式： 由热一律知： dU=Q-  W=  Q-PdV 由热二律知：  Q=TdS 由上述二式推出：dU=TdS-PdV 式(3-2) ：由H=U+PV知： dH=dU+d(PV) =dU+VdP+PdV =TdS-PdV+VdP+PdV =TdS+VdP

注意以下几点 四大微分方程的应用： 恒组分，恒质量体系一封闭体系 ●均相体系（单相） ●平衡态间的变化 ●常用于1mol性质

注意以下几点 ▪ 四大微分方程的应用： •恒组分，恒质量体系——封闭体系 •均相体系（单相） •平衡态间的变化 •常用于1mol性质

3.1.2 点函数间的数学关系 ●点函数 点函数就是函数能够通过自变量在图上用点表示出来的函数， Z=f(x,y） 微分得 z),+ dy dz=Mdx+Nd y (3-5) 在x不变时，M对y求偏微分： ) 在y不变时，N对x求偏微分： () 对于连续函数： 02z82 axay oyax →(x) (3-6)

在y不变时，N对x求偏微分： dy y Z dx x Z dZ y x            +        = x x y x z y y M                   =           =    x y z 2 y y x y z x x N                      =        y x z    2 Z=f(x,y) d z = M d x + N d y (3-5) 在x不变时，M对y求偏微分： 对于连续函数： x y x N y M         =           (3-6) 3.1.2 点函数间的数学关系 •点函数 点函数就是函数能够通过自变量在图上用点表示出来的函数. 微分得

(2)变量关系式 通过点函数的隐函数形式推出：p(x,y,z)=0 do dx+ dz 0 若x不变，则dx=0 (dz)=0 00 02 Ox 同理可得： op op ay a

(2)变量关系式 通过点函数的隐函数形式推出：(x,y,z)=0  = 0        +            +        = dz z dy y dx x d     若x不变，则dx=0 ( ) ( ) = 0        +           x x dz z dy y                      = −        y z x   z y 同理可得：                    = −        y x x z y                     = −           x y y x z    = −1                          z x y x z z y y x

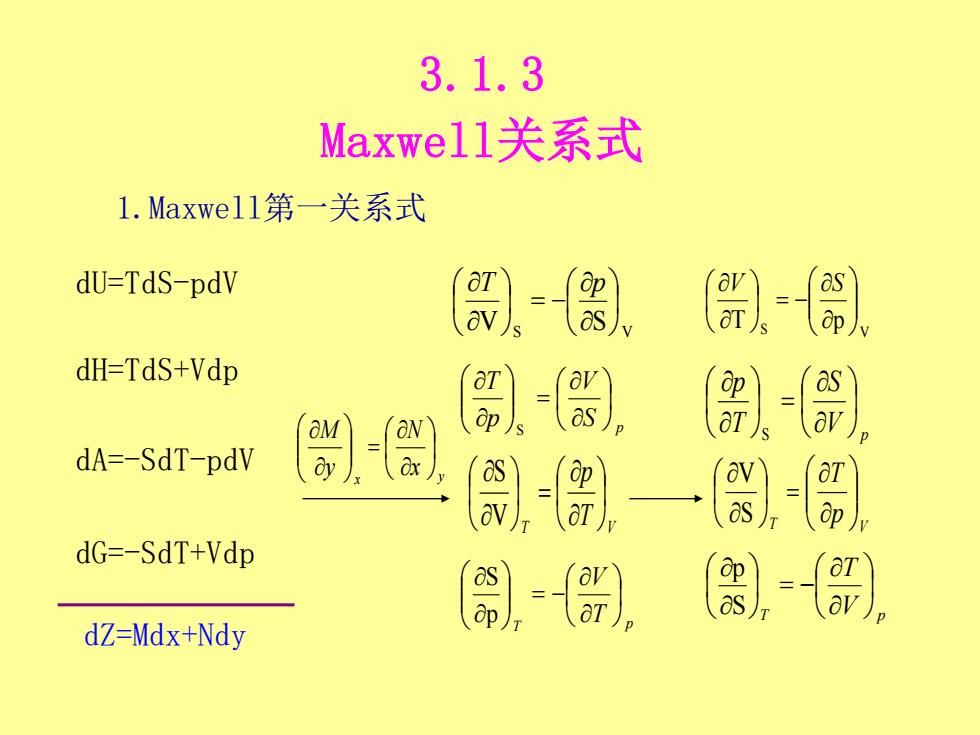
3.1.3 Maxwel1l关系式 1.Maxwell第一关系式 dU-TdS-pdV dH-TdS+Vdp as aN dA=-SdT-pdV 1 av dG=-SdT+Vdp dZ=Mdx+Ndy

3.1.3 Maxwell关系式 1.Maxwell第一关系式 V S S V          = −       T p p S V p T         =           S T V T p          =        V S T T p V         = −           p S S V T p            = −       V S V p S T p          =        S T V p T            =        S V T V p T          = −        S p x y x N y M         =           dU=TdS-pdV dH=TdS+Vdp dA=-SdT-pdV dG=-SdT+Vdp dZ=Mdx+Ndy