上游充廷大¥ Forces on gears Forces on helical gears 上游文大学 FANGHAI HO TONG UNIVERSITY B--B. B-E
6 Forces on gears Forces on helical gears
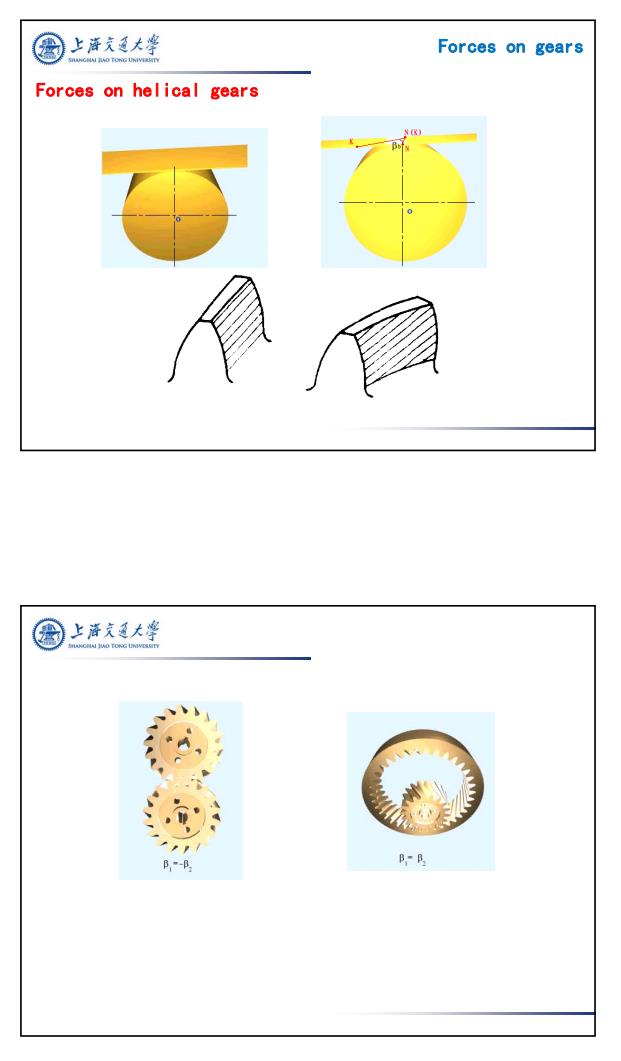
Normal circular pitch Transverse circular pitch (a) =P,Cos攻 Section B-B Helix angle Axial pitch P Px= tan Normal diametral pitch (b) P= PTransverse diametral pitch cos cos女= tan中m Normal pressure angle tan -Transverse pressure ang (e) SectionA-A 上游文大学 FANGHAI HO TONG UNIVERSITY Φn cos= tan n tan
7 Normal circular pitch Transverse circular pitch Helix angle Axial pitch Normal diametral pitch Transverse diametral pitch Normal pressure angle Transverse pressure ang Φn h A' C O ' h Φt O A ψ

上海久通大¥ NO Nomenclatures formulus 1 摄置装装eodu m.is standardized m 2 型e B=820° 3 ransverse presourg,angle 端面压力角 =aretga.is standardized 4 pitch Diameterd、d 分度圆直径 4=m=m, cosB d=m2=m点 Addendum 齿顶高 b。 五。=研、 6 Dedendum hr b,=1.25m, 背我 k=在,十A,=2.25m, 8 蜀e e Gah,-h。=0.25m。 ddendum diamate、da 齿顶圆直经 d1d1+24,d.:sd:+2h。 9 edendum diamete,、da 齿根图直径 d:=d1-2克,d,2=d-2, 2 Central distance a a=d十生=n白,+)=m3+) 中心距 2 2 cosp 上游久通大学 Forces on gears ANGHAI HAO TONG UNIVEROIT Forces on helical gears 斜齿圆柱齿轮传动受力分析 12 0
8 Forces on gears Forces on helical gears
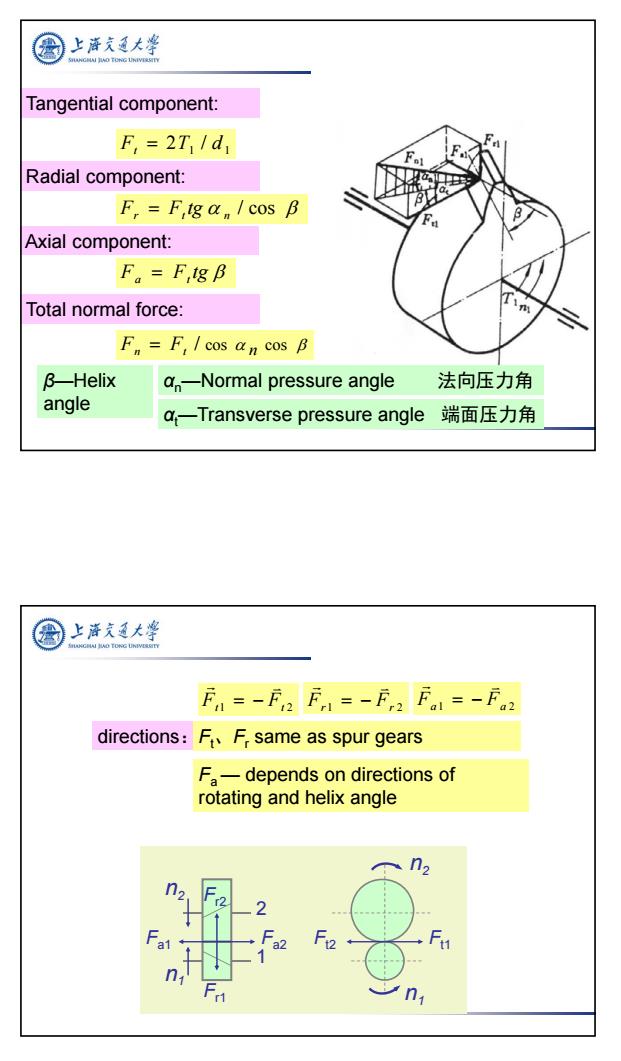
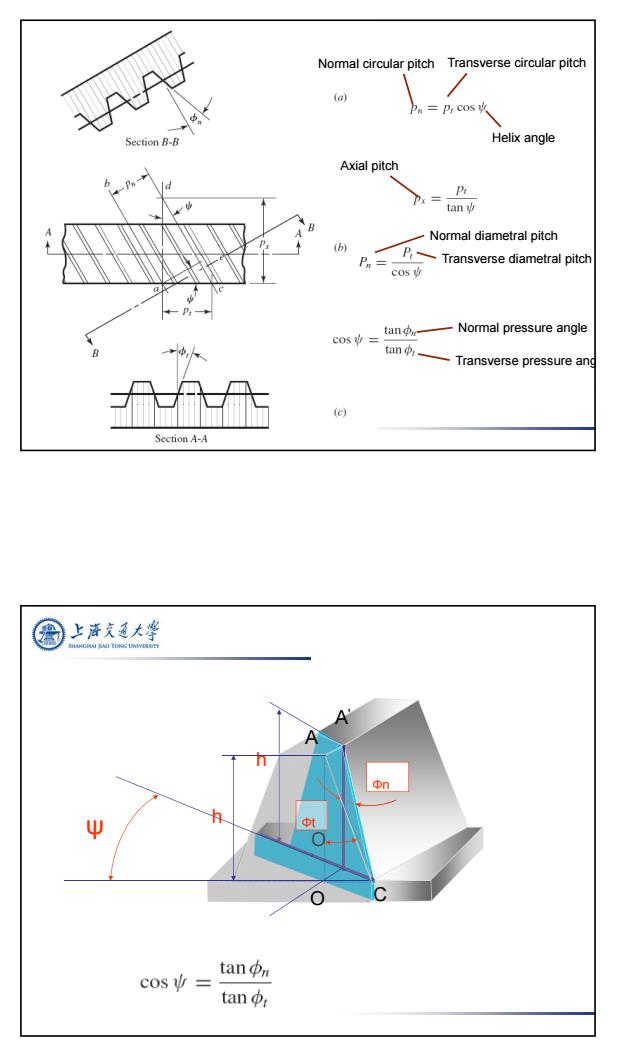
上游久通大学 Tangential component: F,=2T/d1 Radial component: F.F,tg a cos B Axial component: F。=F,gB Total normal force: F=F/cos an cos B B-Helix an-Normal pressure angle 法向压力角 angle a,一Transverse pressure angle端面压力角 上游文大学 f=-F2F,1=-f2F1=-F2 directions:FF same as spur gears Fa-depends on directions of rotating and helix angle F 01
9 Tangential component: 1 1 Ft 2T / d Fr Ft tg n / cos Fa Ft tg / cos cos Fn Ft n αn—Normal pressure angle 法向压力角 αt —Transverse pressure angle 端面压力角 β—Helix angle Radial component: Axial component: Total normal force: 2 1 Ft1 Ft 2 Fr 1 Fr 2 directions:Ft 、Fr same as spur gears Fa — depends on directions of rotating and helix angle Fa1 Fa 2 n2 n1 Fr2 Fr1 Ft2 Ft1 n1 n2 Fa1 Fa2
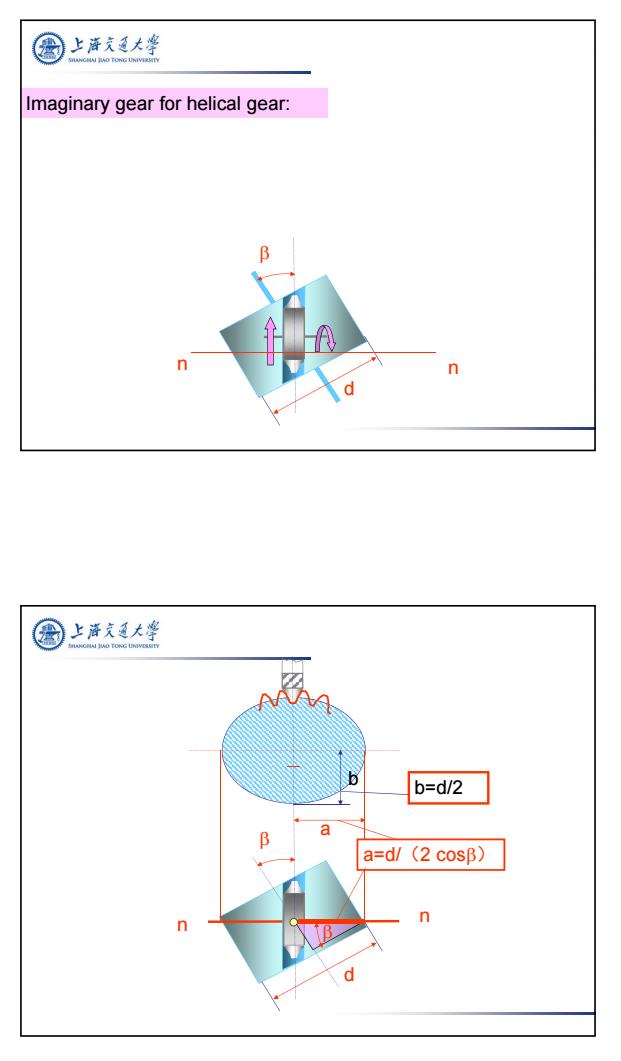
上泽克通大¥ Imaginary gear for helical gear: B 1 n n 上游文大学 ANGHAI HAO TONG UNIVERSITY b=d/2 a B a=d/(2 cosB) n n d
10 d n n Imaginary gear for helical gear: d n n b=d/2 a=d/(2 cos) a b