
Analog Modulation SSB-AM
Analog Modulation SSB – AM

SSB-AM Single Side Band Vs.Double Side Band Remove one side band from DSB USSB(Upper SSB) ■LSSB(Lower SSB) W SSB-AM ↑U(f) M(f) 2W A AAC/2 -W 0 W f。 USSB LSSB USSB :
SSB – AM ◼ Single Side Band Vs. Double Side Band ◼ Remove one side band from DSB ◼ USSB (Upper SSB) ◼ LSSB (Lower SSB) -W 0 W f M(f) f U(f) fc -fc 2W SSB-AM A AAc2 /2 USSB LSSB USSB W
SSB from complex envelope Using complex envelope(analytic function) ■z(t)=A[m(t)±jm(t)] ■USSB-AM u(t)=A.[m(t)cos(2πft)-m(t)sin(2πft)] ■LSSB-AM u(t)=A[m(t)cos(2πft)+m(t)sin(2πft)] 90°Phase shift Hilbert transform of m(t) m(t) h()=1/πt 三m(t)*(1/πt) H(f)=-jsgn(f) =m(t)*h(t) F[H(m(t)]M(f)H(f)
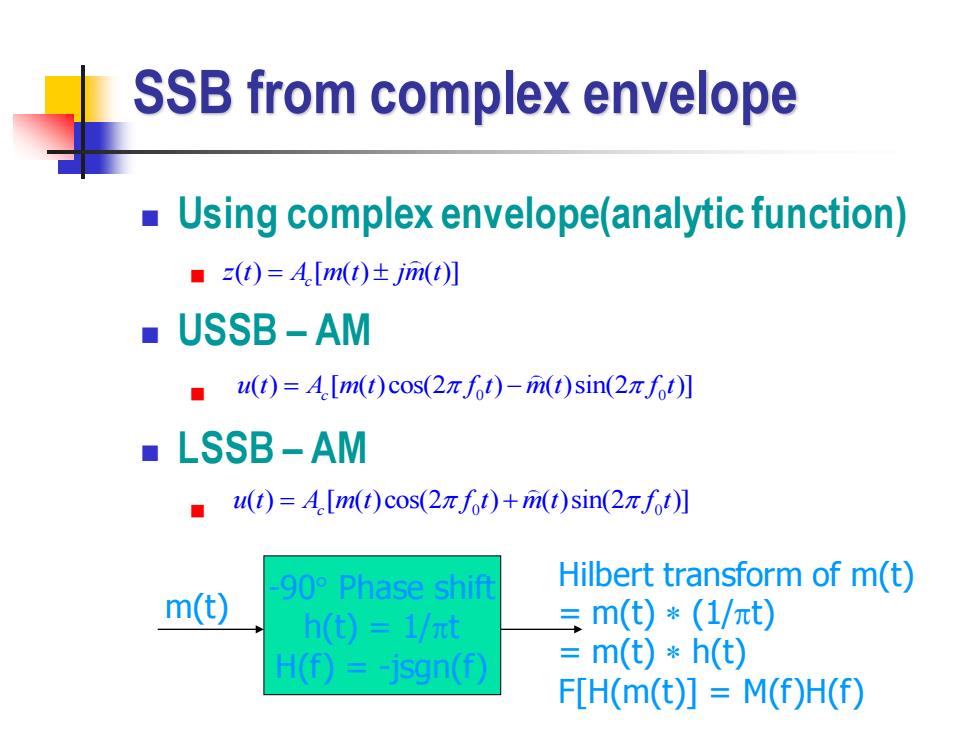
SSB from complex envelope ◼ Using complex envelope(analytic function) ◼ ◼ USSB – AM ◼ ◼ LSSB – AM ◼ ( ) [ ( ) ( )] c z t A m t jm t = 0 0 ( ) [ ( )cos(2 ) ( )sin(2 )] u t A m t f t m t f t = − c -90 Phase shift h(t) = 1/t H(f) = -jsgn(f) m(t) Hilbert transform of m(t) = m(t) (1/t) = m(t) h(t) F[H(m(t)] = M(f)H(f) 0 0 ( ) [ ( )cos(2 ) ( )sin(2 )] u t A m t f t m t f t = + c

SSB in frequency domain ■Take FT of z()t Z(f)=F[z(t)]=F[A {m(t)+jm(t);] =A.{M(f)±jf[m(t]}=A{M(f)±jM(f)H(f)} ■USSB Z(f)=A.(M(f)+jM(fH(=AM(f)(1+j(-jsgn(f))) 2AM(f),f>0 0, f<0 In bandpass ·UsU)=[Zf-f)+Z*(f+f】 A.M(f-f),f>f.[0,f>-f. 0,f<f AM(f+f),f<-f
SSB in frequency domain ◼ Take FT of z(t) ◼ ◼ USSB ◼ ◼ In bandpass ◼ ( ) [ ( )] [ { ( ) ( )}] { ( ) [ ( )]} { ( ) ( ) ( )} c c c Z f F z t F A m t jm t A M f jF m t A M f jM f H f = = = = ( ) { ( ) ( ) ( )} ( ){1 ( sgn( ))} 2 ( ), 0 0, 0 c c c Z f A M f jM f H f A M f j j f A M f f f = + = + − = 1 ( ) [ ( ) * ( )] 2 ( ), 0, 0, ( ), USSB c c c c c c c c c c U f Z f f Z f f A M f f f f f f f f A M f f f f = − + + − − = + + −

SSB in frequency domain ■LSSB Z(f)=A.(M(f)-jM(fH(f))=4.M(f)(1-j(-jsgn(f))) 0, f>0 2A.M(f), f<0 In bandpass ·Um)=)Zf-f)+Z*(f-f】 0, f>f,∫AM(f+f),f>-f A.M(f-f),f<f0, f<-fo Check the difference between text book and this result Scale difference
SSB in frequency domain ◼ LSSB ◼ ◼ In bandpass ◼ ◼ Check the difference between text book and this result ◼ Scale difference ( ) { ( ) ( ) ( )} ( ){1 ( sgn( ))} 0, 0 2 ( ), 0 c c c Z f A M f jM f H f A M f j j f f A M f f = − = − − = 1 ( ) [ ( ) * ( )] 2 0, ( ), ( ), 0, LSSB c c c c c c c c c c U f Z f f Z f f f f A M f f f f A M f f f f f f = − + − + − = + − −