
光学测量技术实验第1章 2.设计性实验内容 根据现有实验条件,设计实验方案探索分析乙醇汽油溶液的浓度与吸光度的关系。 实验要求为:闸述实验基本原理和方法,说明测量系统组成和基本实验步骤,进行实 际实验测量,选择合理方法处理实验数据,分析与讨论实验结果。 【注意事项】 (1)光栅光谱仪属于贵重精密仪器,超出说明书使用操作时需在教师指导下进行。 (2)狭缝宽度的调节必须小心,且狭缝的宽度不得超过3mm,也不得完全闭合,以免 损坏刀口。实验完毕后,应将狭缝宽度调节到0.2mm左右。 (3)在测量吸收曲线或吸光度-介质厚度关系曲线时,要保证仪器各参数(如狭缝宽 度、光电倍增管工作电压等)不变。 (4)光电倍增管受强光照射时会引发“雪崩效应”,测量时入射光不能太强。 【思考与讨论】 (1)光枥光谱仪波长示值的校准为什么要用汞灯?吸收曲线的测量为什么要用溴 钨灯? (2)试讨论陕缝宽度对测量的影响 (3)吸收光谱和发射光谱的关系是什么? (4)如何测量吸光度? 【参考文献】 [1]邓勃,李玉珍,刘明钟.实用原子光谱分析.北京:化学工业出版社,2013. 「2门杨春昆,幸国华,徐秋心.原子光普分析北京:化学工业出版社,2010 [3]王秉超.大学物理实验(下册).北京:高等教育出版社,2003】 实验1-3超声光栅测量液体中的声速 1932年,美国德拜(P.J.W.Debye)和席尔斯(.W.Sears)以及法国卢卡斯(R.Lu cas)和比卡尔(P.Biquand)分别独立地观察到光在超声波传播的液体中的衍射现象,后来 人们在超声波传插的透明固体中也发现了光衍射现象,这种现象称为声光效应(acouste0 optic effect)。声光效应一般是指光通过受到超声波扰动的介质时发生衍射的现象。20 世纪60年代激光的问世促进了声光效应理论和应用研究的迅速发展,声光效应为控制激 光的频率、方向和强度提供了一种有效的手段,大大扩展了激光的应用领域。利用声光效 应制成的声光器件(acousto-optic devices)如声光调制器、声光可调谐滤器、声光偏转器 等,在激光技术、光信号处理和集成光通信技术等方面有着重要的应用。声光效应还有许 多其他重要应用,如声光频谱分析器和声光信号相关器早已在射电望远镜和微被雷达信 号处理中得到广泛应用,利用声光效应可以探测材料声学性质等。 11
— 11 — 2.设计性实验内容 根据现有实验条件,设计实验方案探索分析乙醇汽油溶液的浓度与吸光度的关系. 实验要求为:阐述实验基本原理和方法,说明测量系统组成和基本实验步骤,进行实 际实验测量,选择合理方法处理实验数据,分析与讨论实验结果. 【注意事项】 (1)光栅光谱仪属于贵重精密仪器,超出说明书使用操作时需在教师指导下进行. (2)狭缝宽度的调节必须小心,且狭缝的宽度不得超过3mm,也不得完全闭合,以免 损坏刀口.实验完毕后,应将狭缝宽度调节到0.2mm 左右. (3)在测量吸收曲线或吸光度G介质厚度关系曲线时,要保证仪器各参数(如狭缝宽 度、光电倍增管工作电压等)不变. (4)光电倍增管受强光照射时会引发“雪崩效应”,测量时入射光不能太强. 【思考与讨论】 (1)光栅光谱仪波长示值的校准为什么要用汞灯? 吸收曲线的测量为什么要用溴 钨灯? (2)试讨论狭缝宽度对测量的影响. (3)吸收光谱和发射光谱的关系是什么? (4)如何测量吸光度? 【参考文献】 [1] 邓勃,李玉珍,刘明钟.实用原子光谱分析.北京:化学工业出版社,2013. [2] 杨春晟,李国华,徐秋心.原子光谱分析.北京:化学工业出版社,2010. [3] 王秉超.大学物理实验(下册).北京:高等教育出版社,2003. 实验1G3 超声光栅测量液体中的声速 1932年,美国德拜(P.J.W.Debye)和席尔斯(F.W.Sears)以及法国卢卡斯(R.LuG cas)和比卡尔(P.Biquand)分别独立地观察到光在超声波传播的液体中的衍射现象,后来 人们在超声波传播的透明固体中也发现了光衍射现象,这种现象称为声光效应(acoustoG opticeffect).声光效应一般是指光通过受到超声波扰动的介质时发生衍射的现象.20 世纪60 年代激光的问世促进了声光效应理论和应用研究的迅速发展,声光效应为控制激 光的频率、方向和强度提供了一种有效的手段,大大扩展了激光的应用领域.利用声光效 应制成的声光器件(acoustoGopticdevices)如声光调制器、声光可调谐滤器、声光偏转器 等,在激光技术、光信号处理和集成光通信技术等方面有着重要的应用.声光效应还有许 多其他重要应用,如声光频谱分析器和声光信号相关器早已在射电望远镜和微波雷达信 号处理中得到广泛应用,利用声光效应可以探测材料声学性质等

物理实验教程一近代物理实检 本实验学习声光效应和超声光栅(ultrasonic grating)的基本原理,观察和分析钠黄光 通过超声光栅后的衍射现象,掌握用超声光栅测量透明液体中的声速(acoustic velocity) 的实验方法。 【实验目的】 (1)理解招声光棚的基本原理,学会观测液体中超声光挪的行射现象 (2)掌握超声光栅测量透明液体中声速的原理、方法和实验技术。 (3)了解产生超声波的方法。 【预习要求】 (1)什么是超声光栅? (2)如何调整分光计才能看到衍射条纹? (3)如何利用超声光栅测量液体中的声速 【实验原理】 一、超声光栅的形成原理 超声波是一种机械应力波。当超声波在液体中传插时,液体会周期性地被压缩或膨 胀,使液体的密度发生周期性的变化。压缩作用会使液体的局部密度变大,膨胀作用会使 液体的局部密度变小,液体局部密度的周期性变化会导致液体折射率的周期性变化。 当光波垂直于超声波传播方向通过液体时,不同位置的光波经历的光程不同。原米 是平面被的光波经过液体后,平面波变为弯曲的非平面波,与相位光栅对光的作用相类 似,如图1-3-1所示(图中4为超声波波长)。这种有超声波场的液体称为超声光橱(超声 相位光栅)。光波通过超声光栅时也会发生光栅衍射现象,称为声光衍射(acousto-optic diffraction)。声光衍射是光波与液体中超声波相互作用的结果。 超声波传播方向 质点稀疏区 平面光被之 质点密集区 图1-3-1超声光栅原理示意图 超声行波形成的超声相位光栅,其栅面在空间是随时间移动的。如果超声波在一个 矩形的玻璃液槽中传播,则从液槽的一个平面传播到另一个平面会被反射而沿反方向传 播,人射波和反射波在液体中叠加而形成驻波。在某一时刻,驻波的任一波节两边的质点 都涌向这个节点,使该节点附近形成质点密集区,而相邻的波节处为质点稀疏区:半个周 12
— 12 — 本实验学习声光效应和超声光栅(ultrasonicgrating)的基本原理,观察和分析钠黄光 通过超声光栅后的衍射现象,掌握用超声光栅测量透明液体中的声速(acousticvelocity) 的实验方法. 【实验目的】 (1)理解超声光栅的基本原理,学会观测液体中超声光栅的衍射现象. (2)掌握超声光栅测量透明液体中声速的原理、方法和实验技术. (3)了解产生超声波的方法. 【预习要求】 (1)什么是超声光栅? (2)如何调整分光计才能看到衍射条纹? (3)如何利用超声光栅测量液体中的声速? 【实验原理】 一、超声光栅的形成原理 超声波是一种机械应力波.当超声波在液体中传播时,液体会周期性地被压缩或膨 胀,使液体的密度发生周期性的变化.压缩作用会使液体的局部密度变大,膨胀作用会使 液体的局部密度变小,液体局部密度的周期性变化会导致液体折射率的周期性变化. 当光波垂直于超声波传播方向通过液体时,不同位置的光波经历的光程不同.原来 是平面波的光波经过液体后,平面波变为弯曲的非平面波,与相位光栅对光的作用相类 似,如图1G3G1所示(图中Λ 为超声波波长).这种有超声波场的液体称为超声光栅(超声 相位光栅).光波通过超声光栅时也会发生光栅衍射现象,称为声光衍射(acoustoGoptic diffraction).声光衍射是光波与液体中超声波相互作用的结果. 图1G3G1 超声光栅原理示意图 超声行波形成的超声相位光栅,其栅面在空间是随时间移动的.如果超声波在一个 矩形的玻璃液槽中传播,则从液槽的一个平面传播到另一个平面会被反射而沿反方向传 播,入射波和反射波在液体中叠加而形成驻波.在某一时刻,驻波的任一波节两边的质点 都涌向这个节点,使该节点附近形成质点密集区,而相邻的波节处为质点稀疏区;半个周
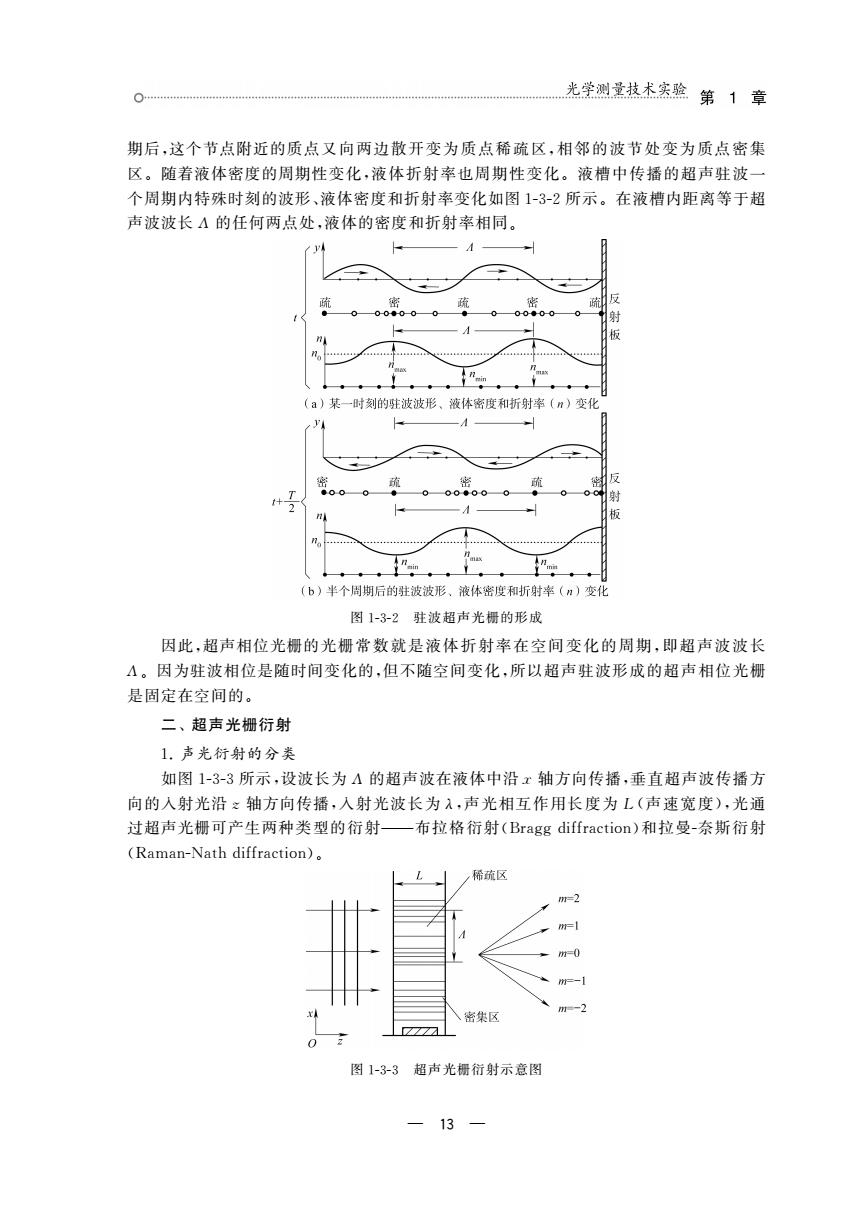
0 光学测量技术实验第1章 期后,这个节点附近的质点又向两边散开变为质点稀疏区,相邻的波节处变为质点密集 区。随着液体密度的周期性变化,液体折射率也周期性变化。液槽中传播的超声驻波一 个周期内特殊时刻的波形、液体密度和折射率变化如图1-32所示。在液槽内距离等于超 声波波长A的任何两点处,液体的密度和折射率相同。 /y4 A 。 (a)某一时刻的班波波形、液体密度和折射率(用)变化 。整。米。一。 ® (b 半个周期后的驻波波形。液体密度折射率()空化 图1-32驻波超声光栅的形成 因此,超声相位光栅的光栅常数就是液体折射率在空间变化的周期,即超声波波长 A。因为驻波相位是随时间变化的,但不随空间变化,所以超声驻波形成的超声相位光栅 是固定在空间的。 二、超声光栅衍射 L.声光衍射的分类 如图1-3-3所示,设波长为A的超声波在液体中沿x轴方向传播,垂直超声波传播方 向的入射光沿:轴方向传播,人射光波长为入,声光相互作用长度为L(声速宽度),光通 过超声光栅可产生两种类型的衍射 -布拉格衍射(Bragg diffraction)和拉曼-奈斯衍射 (Raman-Nath diffraction) 稀流区 图1-3-3超声光栅行射示意图 13
— 13 — 期后,这个节点附近的质点又向两边散开变为质点稀疏区,相邻的波节处变为质点密集 区.随着液体密度的周期性变化,液体折射率也周期性变化.液槽中传播的超声驻波一 个周期内特殊时刻的波形、液体密度和折射率变化如图1G3G2所示.在液槽内距离等于超 声波波长Λ 的任何两点处,液体的密度和折射率相同. 图1G3G2 驻波超声光栅的形成 因此,超声相位光栅的光栅常数就是液体折射率在空间变化的周期,即超声波波长 Λ.因为驻波相位是随时间变化的,但不随空间变化,所以超声驻波形成的超声相位光栅 是固定在空间的. 二、超声光栅衍射 1.声光衍射的分类 如图1G3G3所示,设波长为Λ 的超声波在液体中沿x 轴方向传播,垂直超声波传播方 向的入射光沿z 轴方向传播,入射光波长为λ,声光相互作用长度为L(声速宽度),光通 过超声光栅可产生两种类型的衍射———布拉格衍射(Braggdiffraction)和拉曼G奈斯衍射 (RamanGNathdiffraction). 图1G3G3 超声光栅衍射示意图

物理实验教程一近代物理失检O ①)当超声波颜率较高、声光相互作用长度较大,满足上→会时,产生布拉格行射。 声光介质相当于一个体光棚,衍射光一般只会产生满足布拉格公式的零级和一级衍射极 大值,且土1级衍射极大值不同时存在。 (②)当超声波颜率较低,声光相互作用长度较小,满足L《时,产生拉曼奈斯衍 射。声光介质相当于一个平面光栅,衍射光一般会产生对称于零级的多级衍射极大值,与 平面光栅的衍射类似。 2.拉曼-奈斯衍射 实验中产生的声光衍射类型为拉曼-奈斯衍射。如图1-3-3所示,设频常为f的超声 波引起液体折射率的周期性变化可表示为: nc,)=-ain2xf-) (1-3-1) 式中,。为液体原来的折射率:△为相对于。的折射率最大变化量。考虑到光在液体 中的传插速度(约10m/s)远大于声波的传播速度(约10m/s),可以认为在液体中由超 声波所形成的疏密周期性分布在光波通过液体的这段时间内是不随时间改变的,因此液 体的折射率仅随位置x而改变,则有: nax)-dsin(经) (1-3-2) 若在超声光栅的入射面上的平行光在时刻的波函数为 y-Aexp(2 (1-3-3) 则光通过厚度为L的液体到达超声光栅出射面时的波函数为: y=Aex即2对片-兴月 (1-3-4) 式中,A为振幅:j为虚数单位:T为周期。将式(1-3-2)代入式(1-3-4)可得: y=Aep2号-+兴ne]} (1-3-5) 若令A'=Aex知-2对”的)则式1-35)变为: y-A'expin] (1-3-6) 根据惠更斯-非涅耳原理,超声光栅出射面上的各点可看作一子光源,衍射角为0。的 衍射光到达屏幕上某点时的振幅A可表示为: A-e+nea (1-3-7) 式中,为沿x轴方向超声光橱的宽度:6为衍射光相对于x轴的方向余弦,即 a=cos(7-)=sin0 (1-3-8) 14
— 14 — (1)当超声波频率较高、声光相互作用长度较大,满足L ≫ Λ2 2πλ 时,产生布拉格衍射. 声光介质相当于一个体光栅,衍射光一般只会产生满足布拉格公式的零级和一级衍射极 大值,且±1级衍射极大值不同时存在. (2)当超声波频率较低、声光相互作用长度较小,满足L ≪ Λ2 2πλ 时,产生拉曼G奈斯衍 射.声光介质相当于一个平面光栅,衍射光一般会产生对称于零级的多级衍射极大值,与 平面光栅的衍射类似. 2.拉曼G奈斯衍射 实验中产生的声光衍射类型为拉曼G奈斯衍射.如图1G3G3所示,设频率为f 的超声 波引起液体折射率的周期性变化可表示为: n(x,t)=n0 -Δnsin(2πft- 2π Λ x) (1G3G1) 式中,n0 为液体原来的折射率;Δn 为相对于n0 的折射率最大变化量.考虑到光在液体 中的传播速度(约108 m/s)远大于声波的传播速度(约103 m/s),可以认为在液体中由超 声波所形成的疏密周期性分布在光波通过液体的这段时间内是不随时间改变的,因此液 体的折射率仅随位置x 而改变,则有: n(x)=n0 -Δnsin( 2π Λ x) (1G3G2) 若在超声光栅的入射面上的平行光在t时刻的波函数为: y=Aexp(2πj t T ) (1G3G3) 则光通过厚度为L 的液体到达超声光栅出射面时的波函数为: y=Aexp 2πj( t T - n λ L) é ë ê ê ù û ú ú (1G3G4) 式中,A 为振幅;j为虚数单位;T 为周期.将式(1G3G2)代入式(1G3G4)可得: y=Aexp{2πj t T - n0L λ + ΔnL λ sin(2π x Λ ) é ë ê ê ù û ú ú } (1G3G5) 若令A′=Aexp(-2πj n0L λ ) ,则式(1G3G5)变为: y=A′exp{2πj t T + ΔnL λ sin(2π x Λ ) é ë ê ê ù û ú ú } (1G3G6) 根据惠更斯G菲涅耳原理,超声光栅出射面上的各点可看作一子光源,衍射角为θk 的 衍射光到达屏幕上某点时的振幅AS 可表示为: AS =∫ a 2 - a 2 A′exp{2πj xδ λ + ΔnL λ sin(2π x Λ ) é ë ê ê ù û ú ú }dx (1G3G7) 式中,a 为沿x 轴方向超声光栅的宽度;δ 为衍射光相对于x 轴的方向余弦,即 δ=cos( π 2 -θk ) =sinθk (1G3G8)

光学测量技术实验第1章 再令 “=贸 (1-3-9 0-2x4L (1-3-10) 6- (1-3-11) 则式(1-3-7)可简化为: A.-A'expfj[ur+vsin(br)]dr (1-3-12) 根据欧拉公式,式(1-3-12)可转化为: As(+vsin(r+sinr+vsin(br)]d (1-3-13) 式(1-313)的积分包括实数部分和虚数部分。根据光学相关知识,光波的振幅仅需讨论 实数部分,其展开式为 A(cos(ur)co[wsin(r)]-sin(urd)sin[vsin(hr )])dr (1-3-14) 根据第一类贝塞尔函数的生成函数可有: cosLvsin(br]2Jco(2mbr) (1-3-15) sin[vsin(br)]-2>Jzmtsin[(2m+1)bx] (1-3-16) 将式(1-3-15)和式(1-3-16)代入式(1-3-14)并积分,则有: A-2-ms2+a20} (u6-2mb)a/2 (1-3-17) 2n6222+2222到 [u6-(2m+1)b]a/2 由四血二=1可知,式(13-17)中的每项只有当分母趋于0时才能得到极大值。用 是表示2m及2m+1,则有: u6士kb=0 (1-3-18) 由式(1-3-8)~式(1-3-11)和式(1-3-18)可得: Asin0=±ka k=0,1,2,. (1-3-19) 式(1-3-19)为超声光栅拉曼-奈斯衍射的光强极大条件,该式与光学平面光栅衍射的极大 条件在形式上完全相同。由此可见,当超声波在液体中传播时液体起到了与光学平面光 栅类似的作用,因而有超声波传播的液体被称为超声光栅。根据式(1-319)可知,超声光 栅所对应的光栅常数即为超声波波长A。 当衍射角0。很小时,式(1-3-19)可近似为: A0≈士k入 k=0,1,2. (1-3-20) -15
— 15 — 再令 u= 2π λ (1G3G9) v= 2πΔnL λ (1G3G10) b= 2π Λ (1G3G11) 则式(1G3G7)可简化为: AS =∫ a 2 - a 2 A′exp{j[uxδ+vsin(bx)]}dx (1G3G12) 根据欧拉公式,式(1G3G12)可转化为: AS =∫ a 2 - a 2 {cos[uxδ+vsin(bx)]+jsin[uxδ+vsin(bx)]}dx (1G3G13) 式(1G3G13)的积分包括实数部分和虚数部分.根据光学相关知识,光波的振幅仅需讨论 实数部分,其展开式为: ASR =∫ a 2 - a 2 {cos(uxδ)cos[vsin(bx)]-sin(uxδ)sin[vsin(bx)]}dx (1G3G14) 根据第一类贝塞尔函数J的生成函数可有: cos[vsin(bx)]=2∑ ∞ m=0 J2mcos(2mbx) (1G3G15) sin[vsin(bx)]=2∑ ∞ m=0 J2m+1sin[(2m +1)bx] (1G3G16) 将式(1G3G15)和式(1G3G16)代入式(1G3G14)并积分,则有: ASR =a∑ ¥ m=0 J2m sin[(uδ+2mb)a/2] (uδ+2mb)a/2 + sin[(uδ-2mb)a/2] { (uδ-2mb)a/2 } - a∑ ¥ m=0 J2m+1 sin{[uδ+ (2m +1)b]a/2} [uδ+ (2m +1)b]a/2 + sin{[uδ- (2m +1)b]a/2} { [uδ- (2m +1)b]a/2 } (1G3G17) 由limx→0 sinx x =1可知,式(1G3G17)中的每项只有当分母趋于0时才能得到极大值.用 k 表示2m 及2m+1,则有: uδ±kb=0 (1G3G18) 由式(1G3G8)~式(1G3G11)和式(1G3G18)可得: Λsinθk =±kλ k=0,1,2, (1G3G19) 式(1G3G19)为超声光栅拉曼G奈斯衍射的光强极大条件,该式与光学平面光栅衍射的极大 条件在形式上完全相同.由此可见,当超声波在液体中传播时液体起到了与光学平面光 栅类似的作用,因而有超声波传播的液体被称为超声光栅.根据式(1G3G19)可知,超声光 栅所对应的光栅常数即为超声波波长Λ. 当衍射角θk 很小时,式(1G3G19)可近似为: Λθk ≈±kλ k=0,1,2, (1G3G20)