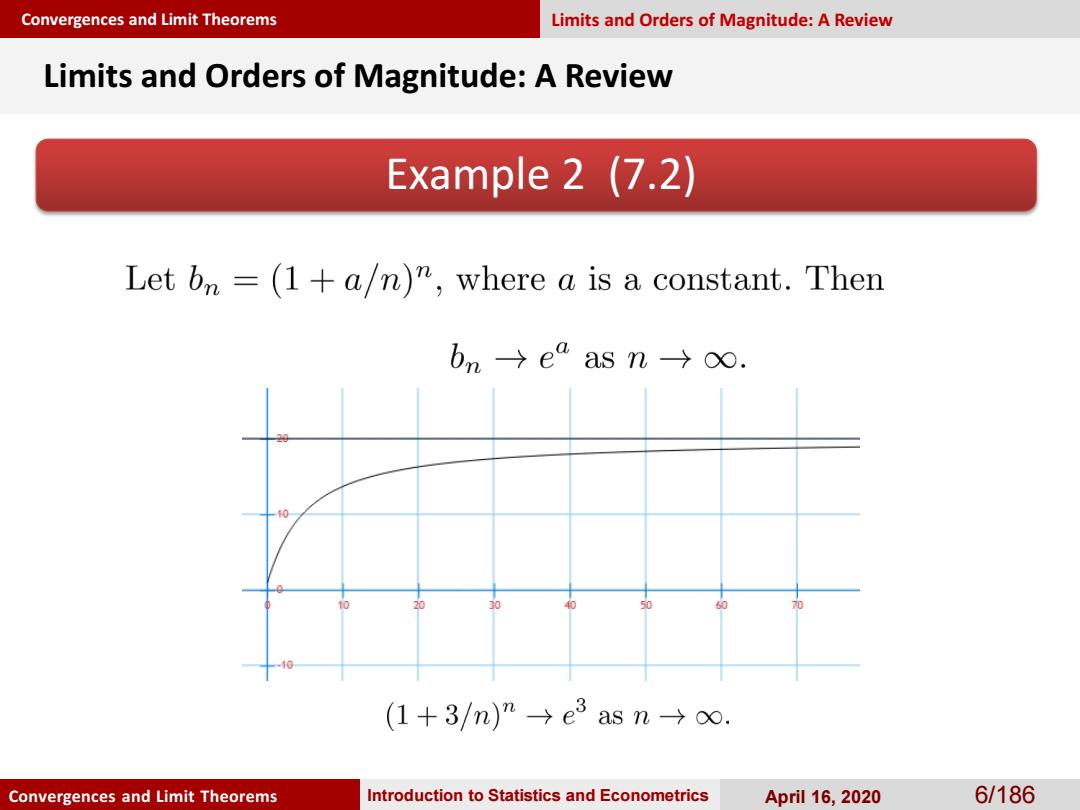
Convergences and Limit Theorems Limits and Orders of Magnitude:A Review Limits and Orders of Magnitude:A Review Example 2 (7.2) Let on=(1+a/n)",where a is a constant.Then bn→ea as n→o. 40 (1+3/m)n→e3asn→o. Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16,2020 6/186
Convergences and Limit Theorems Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16, 2020 6/186 Example 2 (7.2) Limits and Orders of Magnitude: A Review Limits and Orders of Magnitude: A Review

Convergences and Limit Theorems Limits and Orders of Magnitude:A Review Limits and Orders of Magnitude:A Review Example 3 (7.3) on=(-1)".Then fon,n 1,2,...}is bounded by a constant in the sense that on<M for some constant M>1 and for all n 1.However,its limit does not exist. Solution Set e=.Then there exist no b and N(e)such that for all n >N(e),we can have bn -b<e. Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16,2020 7/186
Convergences and Limit Theorems Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16, 2020 7/186 Example 3 (7.3) Limits and Orders of Magnitude: A Review Limits and Orders of Magnitude: A Review Solution

Convergences and Limit Theorems Limits and Orders of Magnitude:A Review Limits and Orders of Magnitude:A Review Definition 2 (7.2).[Continuity] The function g:R->R is continuous at point b if for any sequence{bn}such that on→basn→o,we have g(bn)→g(b)asn→o. Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16,2020 8/186
Convergences and Limit Theorems Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16, 2020 8/186 Definition 2 (7.2). [Continuity] Limits and Orders of Magnitude: A Review Limits and Orders of Magnitude: A Review

Convergences and Limit Theorems Limits and Orders of Magnitude:A Review Limits and Orders of Magnitude:A Review Remarks: An alternative but equivalent definition of continuity: for each given e>0 there exists a 6=(e)such that whenever on-bl 6,we have lg(on)-g(b)<c. When g()is continuous at b,we can write im。g6n)=gibm)=g6). n→oa In other words,the limit of a sequence of values for a continuous function is equal to the value of the function at the limit. Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16,2020 9/186
Convergences and Limit Theorems Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16, 2020 9/186 Limits and Orders of Magnitude: A Review Limits and Orders of Magnitude: A Review Remarks:

Convergences and Limit Theorems Limits and Orders of Magnitude:A Review Limits and Orders of Magnitude:A Review Example 4 (7.4) Suppose an→a and bn→basm→o.Then as n→o, (1)an+bn→a+b; (2)anbn→ab; (3)an/bn→a/bifb≠0. Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16,2020 10/186
Convergences and Limit Theorems Convergences and Limit Theorems Introduction to Statistics and Econometrics April 16, 2020 10/186 Example 4 (7.4) Limits and Orders of Magnitude: A Review Limits and Orders of Magnitude: A Review