
海大理学院放学裸件 大学物理学电子教案 机械能与机械能守恒定律 3-4动能定理 3-5保守力与非保守力势能 3-6功能原理机械能守恒定律
3-4 动能定理 3-5 保守力与非保守力 势能 3-6 功能原理 机械能守恒定律 大学物理学电子教案 海大理学院教学课件 机械能与机械能守恒定律

复习 冲量 i=∫必Fdi 动量定理 7=∫Fd=AP •质点系的动量定理 T=p-p。 •动量守恒定律 P=∑mg,=恒矢量 d dM 变质量物体的运动方程 M dt -F+ dt
复 习 •冲量 2 1 t t I Fdt = •动量定理 I = Fdt=P •质点系的动量定理 P P0 I = - •动量守恒定律 = = 恒矢量 = n i i i P m v 1 •变质量物体的运动方程 dt dM F u dt dv M = +
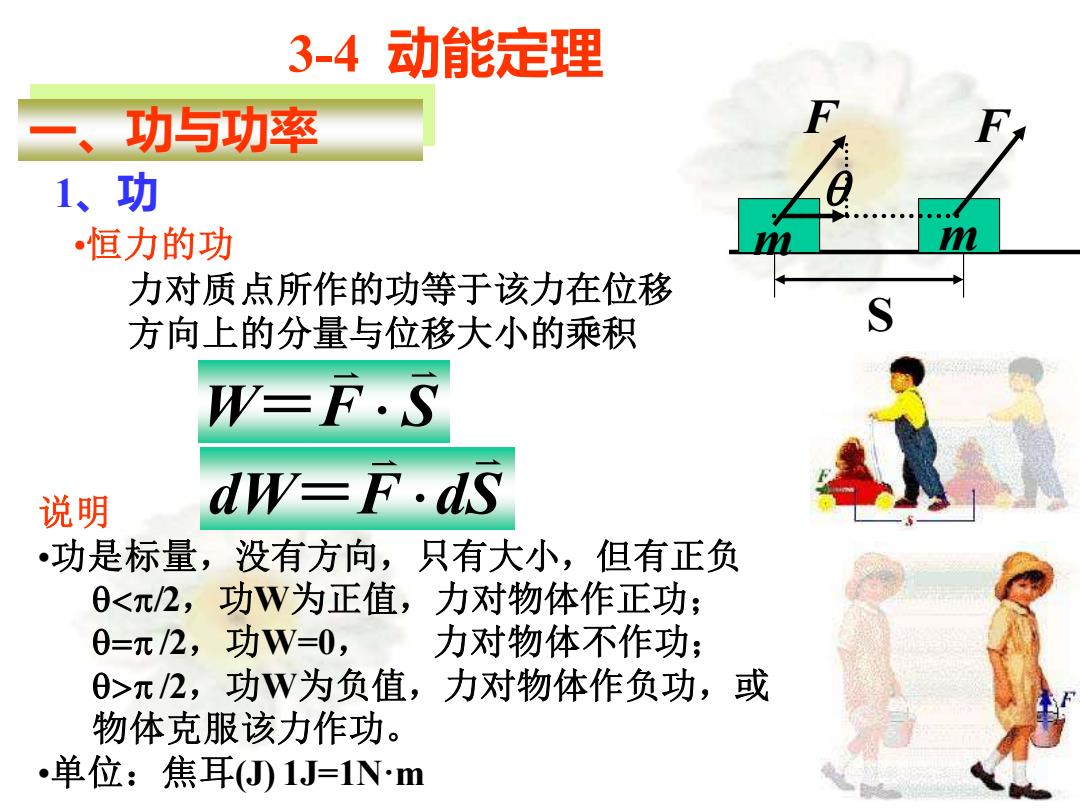
3-4动能定理 功与功率 1、功 恒力的功 力对质点所作的功等于该力在位移 方向上的分量与位移大小的乘积 W=F.S 说明 dW=F.ds 功是标量,没有方向,只有大小,但有正负 0<π/2,功W为正值,力对物体作正功; 0=元/2,功W=0, 力对物体不作功; 0>π2,功W为负值,力对物体作负功,或 物体克服该力作功。 .单位:焦耳(J1J=1Nm
3-4 动能定理 一、功与功率 1、功 •恒力的功 力对质点所作的功等于该力在位移 方向上的分量与位移大小的乘积 W F S = m m F F S 说明 •功是标量,没有方向,只有大小,但有正负 <p/2,功W为正值,力对物体作正功; =p /2,功W=0, 力对物体不作功; >p /2,功W为负值,力对物体作负功,或 物体克服该力作功。 •单位:焦耳(J) 1J=1N·m dW F dS =

变力的功 分成许多微小的位移元,在每一个 位移元内,力所作的功为 dw F.ds F cos0 ds 总功 X w=∫w=∫F,s=∫Fcos0 合力的功 w=∫F.S=∫∑F)S=∑(E·S)=∑W 合力对质点所作的功,等于每个分力所作的功的代数和
•变力的功 分成许多微小的位移元,在每一个 位移元内,力所作的功为 dW = F dS = F cos ds W dW = F dS = F cos ds = 总功 •合力的功 W F dS Fi dS = Fi dS =Wi ( ) ( ) = = 合力对质点所作的功,等于每个分力所作的功的代数和。 O Y X Z b a dr F

功的计算 (1)分析质点受力情况,确定力随位置变化的关系; (2)写出元功的表达式,选定积分变量; (3)确定积分限进行积分,求出总功。 F=Fi+F j+Fk W-(Fdx+F,dy+F.d) dS dxi dyj dzk 例1.设作用在质量为2kg的物体上的力F=6t(N)。如果物体由静 止出发沿直线运动,问在头2s时间内,这个力对物体所作的功。 解:按功的定义式计算功,必须首先求出力和位移的关系式。 根据牛顿第二定律F=a可知物体的加速度为=Fn=6t/2=3t 所以dv=adt=3tdt ∫dw=j3h=1.5r dx vdt 1.5t2dt 力所作的功为W=∫F=∫6t1.5tat=j9rt=36J
•功的计算 (1)分析质点受力情况,确定力随位置变化的关系; (2)写出元功的表达式,选定积分变量; (3)确定积分限进行积分,求出总功。 dS dxi dyj dzk F Fx i Fy j Fz k = + + = + + ( ) W F dx + F dy + F dz = x y z 例1.设作用在质量为2kg的物体上的力F =6t(N)。如果物体由静 止出发沿直线运动,问在头2s时间内,这个力对物体所作的功。 解:按功的定义式计算功,必须首先求出力和位移的关系式。 根据牛顿第二定律F=ma可知物体的加速度为 a=F/m=6t/2=3t 所以 dv=adt=3tdt 2 0 0 dv 3tdt 1.5t v t = = dx vdt t dt 2 = = 1.5 W Fdx 6t 1.5t dt 9t dt 36J 2 0 2 3 = = = = 力所作的功为