北京大学：《燃烧学基础》课程教学资源（讲义）基础燃烧理论课堂讲义（共七章，主讲：陈正）

基础燃烧理论义 陈正（比京大学工学院z@pku.edcm)2014120 6)层流扩散火焰(8课时) 一维扩散火焰模型、Burke-Schumann火焰 Stefan流、液滴蒸发与燃烧 7)层流预混火焰(12课时) 一维平面预混火焰的理论与模拟 拉伸率、火焰稳定性 点火、熄火以及可燃极限 8)其他(6课时) 微尺度燃烧、超声速燃烧、湍流燃烧 公N

基础燃烧理论义 陈正 (北京大学 工学院 cz@pku.edu.cn) 2014/1/20 4 6) 层流扩散火焰 (8 课时) 一维扩散火焰模型、Burke–Schumann 火焰 Stefan 流、液滴蒸发与燃烧 7) 层流预混火焰 (12 课时) 一维平面预混火焰的理论与模拟 拉伸率、火焰稳定性 点火、熄火以及可燃极限 8) 其他 (6 课时) 微尺度燃烧、超声速燃烧、湍流燃烧

基础燃烧理论义 陈正(d北京大学工学院2@pk.edu.cn)2014/120 第2章化学反应热力学 2.1基本概念 >气体混合物 假设混合物的体积为，其中含有N种不同组分，第k种组分的摩尔数和分 子量分别为nx mole和W:g/mole。 组分k的摩尔百分数（体积百分数）定义为： x4= %+%++m,、 组分k的质量百分数定义为： 2形 ynnWy n形 ∑(n,W) 可见：立4=立= 空气中氧气的体积百分数为21%，氮气的体积百分数为79%： 02=21% (5=79% 0:=(021×32)M0.21×32+0.79×28=23.3% 2=(0.79×28)/0.21×32+0.79×28)=76.7% 摩尔百分数转换为质量百分数：y=(x,形)/∑(x用) 质量百分数转换为摩尔百分数：4=(0所：)/空0) 混合物的平均分子量：币=∑(x)=1/∑(y,/W) 分压定律：P=A,R=nRTW=p,RT/W,月=xP,P:=yP 组分长的摩尔浓度为：C=W]-号-号-带，其中M为组分素的分 子式

基础燃烧理论义 陈正 (北京大学 工学院 cz@pku.edu.cn) 2014/1/20 5 第 2 章 化学反应热力学 2.1 基本概念  气体混合物 假设混合物的体积为 V，其中含有 N 种不同组分，第 k 种组分的摩尔数和分 子量分别为 nk mole 和 Wk g/mole。 组分 k 的摩尔百分数(体积百分数) 定义为：       N i i k N k k n n n n n n x 1 1 2 ... 组分 k 的质量百分数定义为：       N i i i k k N N k k k nW n W nW n W n W n W y 1 1 1 2 2 ( ) ... 可见： 1 1 1       N k k N k k x y 空气中氧气的体积百分数为 21%，氮气的体积百分数为 79%：      79% 21% 2 2 N O x x →                (0.79 28)/(0.21 32 0.79 28) 76.7% (0.21 32)/(0.21 32 0.79 28) 23.3% 2 2 N O y y 摩尔百分数转换为质量百分数：   N i k k k i Wi y x W x 1 ( )/ ( ) 质量百分数转换为摩尔百分数：   N i k k k i Wi x y W y 1 ( / )/ ( / ) 混合物的平均分子量：       N i i i N i W xi Wi y W 1 1 ( ) 1/ ( / ) 分压定律：   N k P Pk 1 ， Pk nkR T V kR T Wk / / 0 0    ， Pk  xkP， k  Yk 组分 k 的摩尔浓度为： W x R T x P V n C M k k k k k      0 [ ] ，其中 Mk为组分 k 的分 子式

基础燃烧理论义 陈正（比京大学工学院2@pku.edu.cn)2014/120 >化学反应 C+02C02,H+02→0+0H 化学反应的通用形式：立y:M:~立：M: 其中M为组分k的分子式（如O2,OH,H2O),v为组分k在该反应中作为反 应物的系数，v”为组分k在该反应中作为生成物的系数。定义=k-Vk,则 如果V4=0<即v0,则组分k为反应产物： 如果，>0=，即0，则组分k为反应物： 如果V4="=0,则该反应中不涉及组分： 如果，=">0，则该反应中组分k为第三体（催化剂）。 空气中含有21%的02和79%的N2(体积比)，即1mol02对应79%21%=3.76 mole N2。因此燃料和空气反应通常写成：Fuel+(O2+3.76N2)。 燃料和氧化剂正好完全燃烧： CH4+202+7.52N2→C02+2H20+7.52N H2+0.502+1.88N2→H20+1.88N2 CH02+(x+0.25y-0.5z02+3.76N2→xC02+0.5yH20+3.76x+0.25y-0.5z)N2 其中CH,O,为碳氢燃料的通用表达式。因此完全燃烧1 mole C.H,O,需要 (x+0.25y-0.5z)mole02,对应空气为4.76(x+0.25y-0.5z)mole. 化学反应当量比： 实际燃空比一(F14) 炉化学当量燃空比F1) ，(F/A)。=燃料的量/空气的量 其中FA可以是质量比，也可以是摩尔数之比。另外，由于空气中氧气含量为固 定值，因此有： 品0 其中F代表燃料Fuel),A代表空气(Air),O代表氧气(Oxygen))。 根据化学反应当量比的定义：1时，则燃料与空气/氧气正好完全燃烧 (stoichiometric);1时，则燃料过多而空气/氧气不足(fuel rich)正好完全燃烧： 6

基础燃烧理论义 陈正 (北京大学 工学院 cz@pku.edu.cn) 2014/1/20 6  化学反应 C+O2↔CO2，H+O2↔O+OH 化学反应的通用形式：     N k k k N k k Mk M 1 1  ' " 其中 Mk为组分 k 的分子式(如 O2，OH，H2O…)，ν’k为组分 k 在该反应中作为反 应物的系数，ν”k为组分 k 在该反应中作为生成物的系数。定义 k k k   "  ' ，则： 如果 k k  '  0  " 即 νk>0，则组分 k 为反应产物； 如果 k k  '  0  " 即 νk<0，则组分 k 为反应物； 如果 ' k "k  0 ，则该反应中不涉及组分 k； 如果 ' k "k  0 ，则该反应中组分 k 为第三体(催化剂)。 空气中含有 21%的 O2 和 79%的 N2(体积比)，即 1 mol O2 对应 79%/21%＝3.76 mole N2。因此燃料和空气反应通常写成：Fuel + (O2 + 3.76N2)。 燃料和氧化剂正好完全燃烧： CH4 + 2O2 + 7.52N2 → CO2 + 2H2O + 7.52N2 H2 +0.5O2 + 1.88N2 → H2O + 1.88N2 CxHyOz + (x+0.25y-0.5z)(O2+3.76N2)→xCO2+ 0.5yH2O + 3.76(x+0.25y-0.5z)N2 其中 CxHyOz 为碳氢燃料的通用表达式。因此完全燃烧 1 mole CxHyOz 需要 (x+0.25y-0.5z) mole O2，对应空气为 4.76(x+0.25y-0.5z) mole。 化学反应当量比： F A st F A ( / ) ( / ) ＝ 化学当量燃空比 实际燃空比 ＝ ， (F / A)st  燃料的量 /空气的量 其中 F/A 可以是质量比，也可以是摩尔数之比。另外，由于空气中氧气含量为固 定值，因此有： st F O st F O F A F A ( / ) ( / ) ( / ) ( / ) ＝  其中 F 代表燃料(Fuel)，A 代表空气(Air)，O 代表氧气(Oxygen)。 根据化学反应当量比的定义：=1 时，则燃料与空气/氧气正好完全燃烧 (stoichiometric) ；>1 时，则燃料过多而空气/氧气不足(fuel rich)正好完全燃烧；

基础燃烧理论义 陈正（比京大学工学院2@pku.edu.cn)2014/120 l时，则空气/氧气过多而燃料不足(fuel lean)。 过量空气系数是实际燃烧进入的空气质量与理论燃烧所用的空气质量之比。 因此过量空气系数等于化学反应当量比的倒数。过量空气系数大于1时，混合气 为稀混合气(fuel lean),小于1时为浓混合气(fuel rich), 空燃比是混合气的空气质量与燃油质量之比 空燃比大于14.7时为稀混合气，小于14.7时为浓混合气 >例题： 给定化学反应当量比，配制燃料CH,Oz与空气的混合气： CH,02+(x+0.25y-0.5z(02+3.76N2) 因此燃料、氧气和氮气的体积比/摩尔数之比为： $(x+0.25y-0.5a):3.76(x+0.25y-0.5z) 对应各个组分的体积比为： 0+476x+025y-0.5问 2(x+0.25y-0.5z) xom0+476x+025y-05) 3.76(x+0.25y-0.5z） X70+476x+025y-0.5 >例题： 实验设计，CH/air混合气体，当量比为=0.8 CH4+2(02+3.76N2) 2 a+2×476+2x476-a-

基础燃烧理论义 陈正 (北京大学 工学院 cz@pku.edu.cn) 2014/1/20 7 <1 时，则空气/氧气过多而燃料不足(fuel lean)。 过量空气系数是实际燃烧进入的空气质量与理论燃烧所用的空气质量之比。 因此过量空气系数等于化学反应当量比的倒数。过量空气系数大于 1 时，混合气 为稀混合气(fuel lean)，小于 1 时为浓混合气(fuel rich)。 空燃比是混合气的空气质量与燃油质量之比 空燃比大于 14.7 时为稀混合气，小于 14.7 时为浓混合气  例题： 给定化学反应当量比，配制燃料 CxHyOz 与空气的混合气： CxHyOz + (x+0.25y-0.5z)(O2 + 3.76N2) 因此燃料、氧气和氮气的体积比/摩尔数之比为： : (x+0.25y-0.5z) : 3.76(x+0.25y-0.5z) 对应各个组分的体积比为： 4.76(x 0.25y 0.5z) xFuel      ＝ 4.76( 0.25 0.5 ) ( 0.25 0.5 ) 2 x y z x y z xO       ＝ 4.76( 0.25 0.5 ) 3.76( 0.25 0.5 ) 2 x y z x y z xN       ＝  例题： 实验设计，CH4/air 混合气体，当量比为＝0.8 CH4 + 2(O2 + 3.76N2) 2 4.76 4     xCH ＝ ， 2 4.76 2 2    xO ＝ ， N 2 1 CH 4 O2 x ＝  x  x

基础燃烧理论义 陈正（比京大学工学院z@pk.edu.cn)2014/120 高速摄像机 光学纹影 压力表 实验1：上述预混气体在封闭容器中，初始压力为P-1am。电火花点火导致 的球形火焰向外传播（非定常）。 根据分压定律充气：首先抽真空，压力表显示封闭容器中的压力为P-0am: 接下来充CH4,直到压力表显示压力为P=xcw aim时停止充气：接下来充O2, 直到压力表显示压力为P-(xCHu+2)atm时停止充气：最后充N2,直到压力表显 示压力为P=latm时停止充气。 相机 火焰玻璃管 质量 气体混合容器 流量器 实验山：上述预混气体在开口玻璃管中形成静止的火焰（定常问题）。 采用质量流量计配气，使得CH,N2,O2间的质量流量之比为xC4w2:xo2

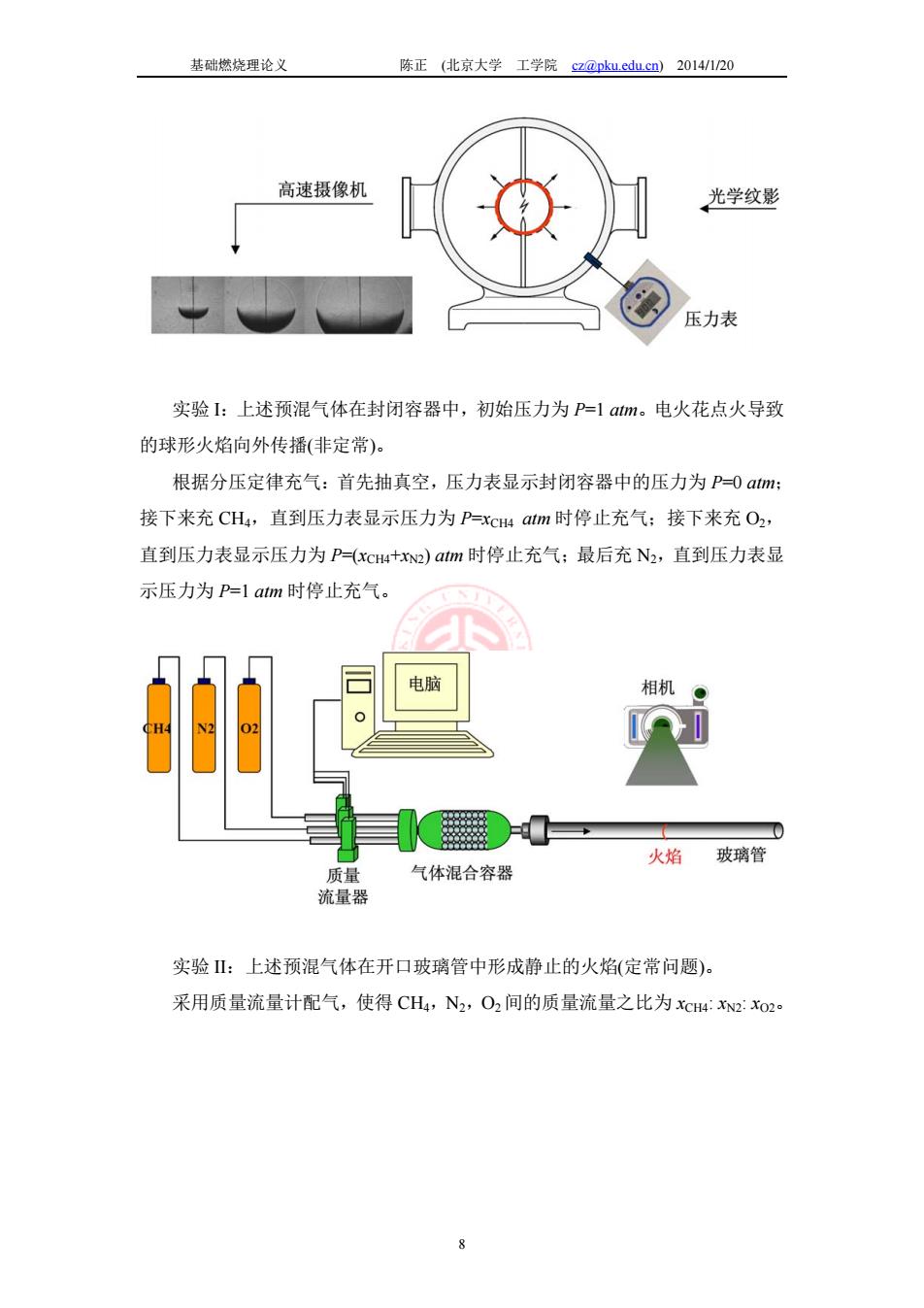
基础燃烧理论义 陈正 (北京大学 工学院 cz@pku.edu.cn) 2014/1/20 8 实验 I：上述预混气体在封闭容器中，初始压力为 P=1 atm。电火花点火导致 的球形火焰向外传播(非定常)。 根据分压定律充气：首先抽真空，压力表显示封闭容器中的压力为 P=0 atm； 接下来充 CH4，直到压力表显示压力为 P=xCH4 atm 时停止充气；接下来充 O2， 直到压力表显示压力为 P=(xCH4+xN2) atm 时停止充气；最后充 N2，直到压力表显 示压力为 P=1 atm 时停止充气。 实验 II：上述预混气体在开口玻璃管中形成静止的火焰(定常问题)。 采用质量流量计配气，使得 CH4，N2，O2 间的质量流量之比为 xCH4: xN2: xO2