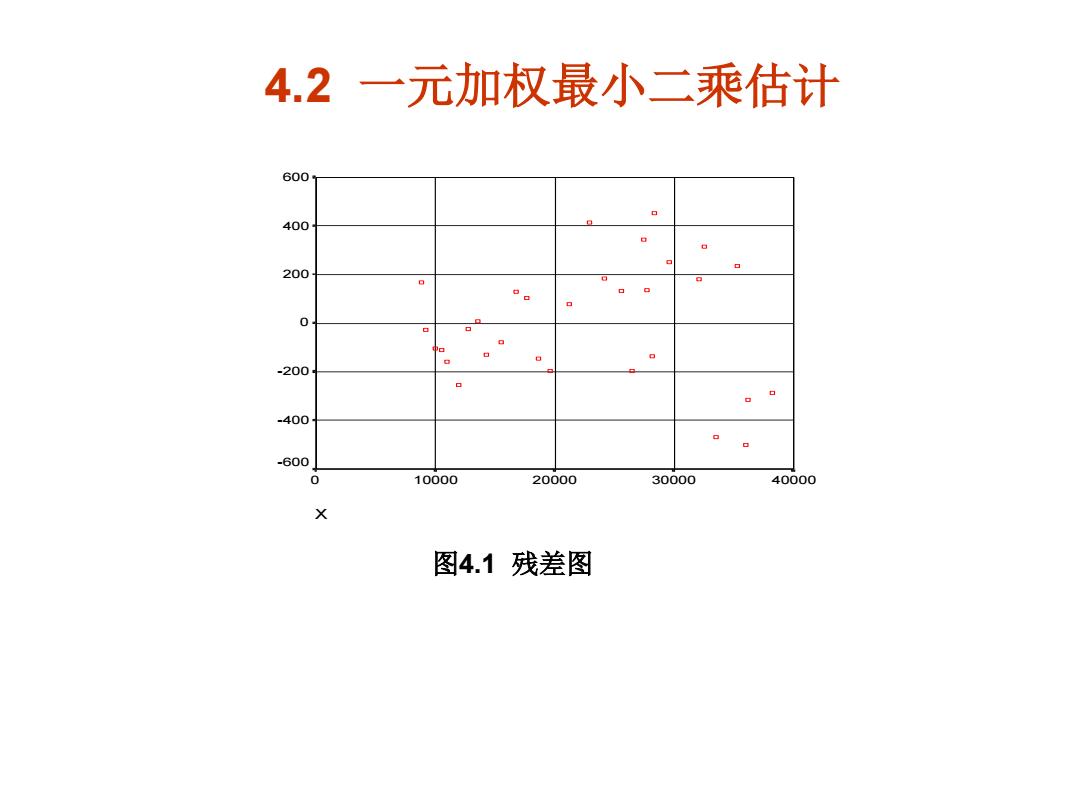
4.2一元加权最小二乘估计 0000 20000 0000 40000 图4.1残差图
4.2 一元加权最小二乘估计 X 0 10000 20000 30000 40000 Unstandardized Residual 600 400 200 0 -200 -400 -600 图4.1 残差图
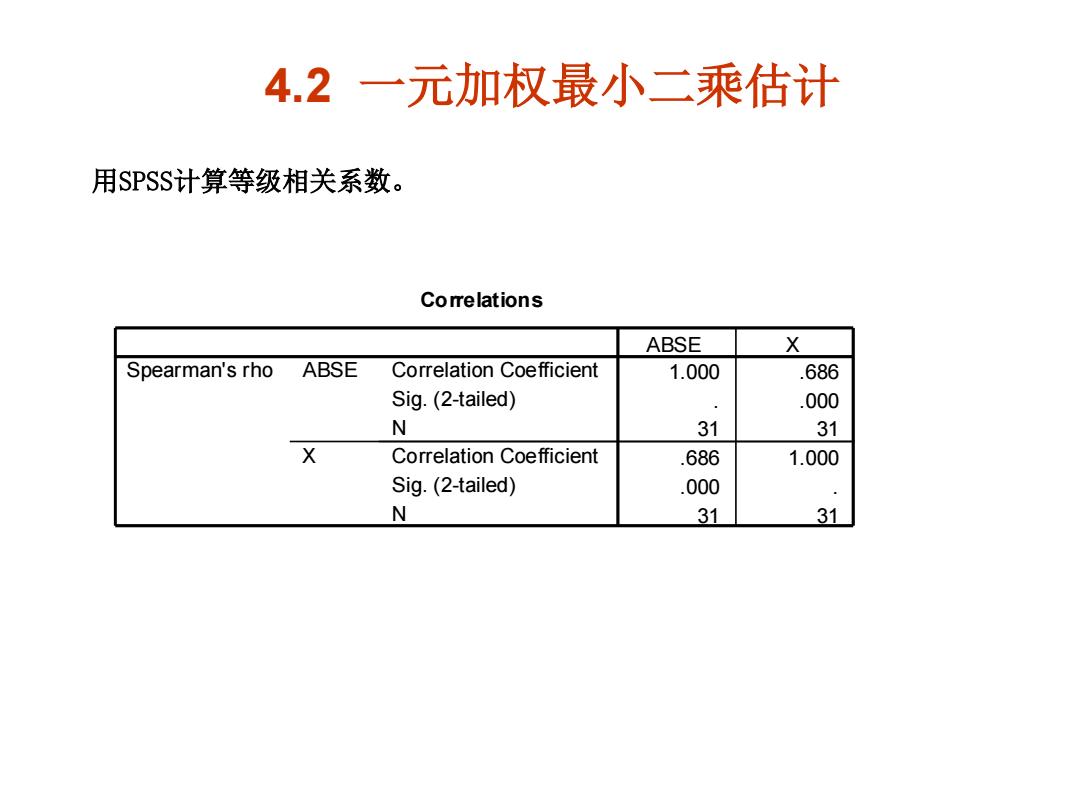
4.2 一元加权最小二乘估计 用SPSS计算等级相关系数。 Correlations ABSE Spearman's rho ABSE Correlation Coefficient 1.000 .686 Sig.(2-tailed) 000 N 31 31 X Correlation Coefficient .686 1.000 Sig.(2-tailed) .000 N 31 31
4.2 一元加权最小二乘估计 用SPSS计算等级相关系数。 Correlations 1.000 .686 . .000 31 31 .686 1.000 .000 . 31 31 Correlation Coefficient Sig. (2-tailed) N Correlation Coefficient Sig. (2-tailed) N ABSE X Spearman's rho ABSE X

4.2一元加权最小二乘估计 (2)计算等级相关系数。 6 r,=1-313-0 ×1558=0.6859 √31-2×0.6859 I= .=5.076 V1-0.68592
4.2 一元加权最小二乘估计 (2)计算等级相关系数。 1558 0.6859 31(31 1) 6 1 2 rs 5.076 1 0.6859 31 2 0.6859 2 t

4.2一元加权最小二乘估计 Spearman等级相关系数可以反映非线性相关的情况, Pearson简单相关系数不能反映非线性相关的情况。 例如x与y的取值如下, 序号12345678910 12345678910 y149162536496481100 y,=x具有完全的曲线相关。 容易计算出y与x的简单相关系数=0.9746, 而y与x的等级相关系数r,=1
4.2 一元加权最小二乘估计 Spearman等级相关系数可以反映非线性相关的情况, Pearson简单相关系数不能反映非线性相关的情况。 例如x与y的取值如下, 序号 1 2 3 4 5 6 7 8 9 10 x 1 2 3 4 5 6 7 8 9 10 y 1 4 9 16 25 36 49 64 81 100 2 i i y x 容易计算出y与x的简单相关系数r=0.9746, 而y与x的等级相关系数rs=1 具有完全的曲线相关

4.2一元加权最小二乘估计 二、一元加权最小二乘估计 消除异方差性的方法通常有: ●加权最小二乘法, ●Box-Cox变换法, ●方差稳定性变换法 加权最小二乘法(Veighted Least Square,简记为WLS) 是一种最常用的消除异方差性的方法
4.2 一元加权最小二乘估计 二、一元加权最小二乘估计 消除异方差性的方法通常有: 加权最小二乘法, Box-Cox变换法, 方差稳定性变换法 加权最小二乘法(Weighted Least Square,简记为WLS) 是一种最常用的消除异方差性的方法