
由于化学反应发生的系统是多元系统,这种系统的自由 焓不仅与温度、压力有关,还与系统中各组分的含量有关。 即:G=Gt(T,P,n1,n2.) dG,=-Sdr+V+∑4,dn, (10-7) 4,=( T. On G-nG dn;=vds dG,=Sdr+Vdp+∑(4,y,de) (10-8) 在恒T,P下,系统的总自由焓变化与反应进度的关系为: (dG)zp=∑(4y,de)或 (10-9) 16
16 i (10-7) N i dG dT dp i dn = = − + + 1 t S V 由于化学反应发生的系统是多元系统,这种系统的自由 焓不仅与温度、压力有关,还与系统中各组分的含量有关。 即:Gt =Gt(T,P,n1,n2.) ∴ j i Gt=nG i T p n t i n G = , , ( ) dn d i = i dGt = SdT Vdp ( d) + + i i (dG ) ( ) t , d T p = i i ( ) ( ) T , p i i Gt = ∵ ∴ (10-8) 在恒T,P下,系统的总自由焓变化与反应进度的关系为: 或 (10-9)
亦即:反应系统的总自由焓随着反应进度的变化率为系统各 组分化学位与其代数计量系数乘积的加和。 若以反应进度为横坐标,系统的总自 由焓为纵坐标,作出总自由焓与反应 T,P一定 进度的关系曲线, 在平衡状态时,应有 0G=0 (10-6) (dG)rp-0 将式(10-6)代入式(10-9)中,得 ∑(4%)=0 (10-10) E E 判断化学平衡的准则
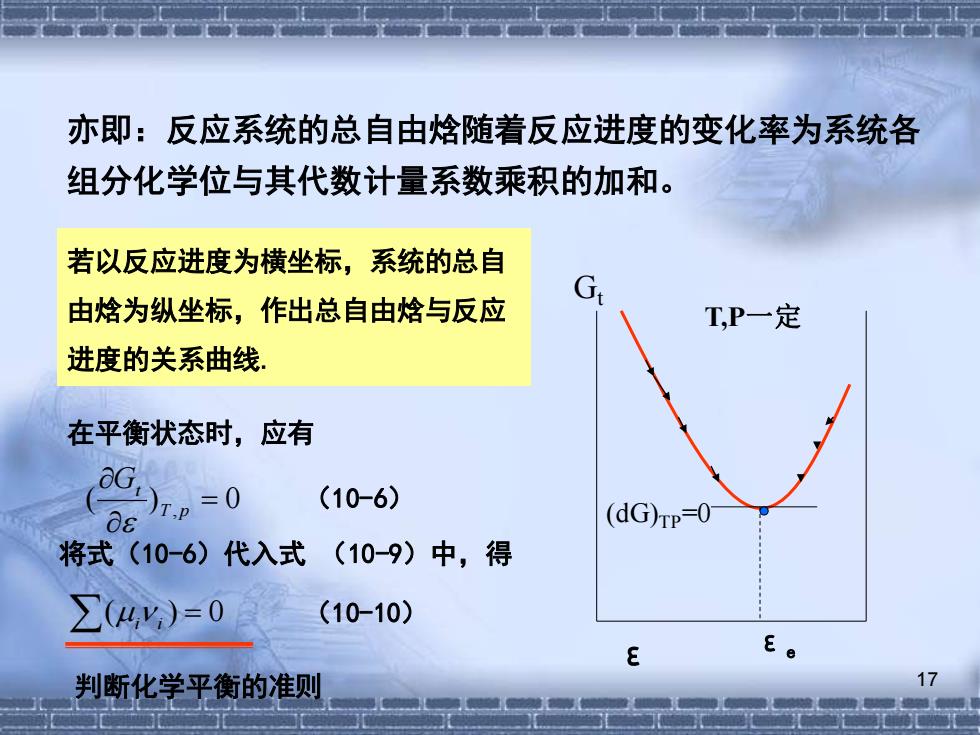
17 亦即:反应系统的总自由焓随着反应进度的变化率为系统各 组分化学位与其代数计量系数乘积的加和。 若以反应进度为横坐标,系统的总自 由焓为纵坐标,作出总自由焓与反应 进度的关系曲线. T,P一定 (dG)TP=0 Gt ε εe 在平衡状态时,应有 ( ) , = 0 T p Gt (10-6) (i i ) = 0 (10-10) 将式(10-6)代入式 (10-9)中,得 判断化学平衡的准则

2.△G与K间的关系 △G一标准自由焓 K一化学平衡常数 (1)关系 前面已经讨论过,化学位与偏摩尔性质是两个独立的概念, 只有当 G1=4时,二者才为同一值。 对于偏摩尔自由焓,它与活度存在有下列关系: G=°,+RT In a, 4,=G°,+RT In a, (10-11) 式中: G,0一组分1在标准态时的自由焓。 18
18 (1)关系 2.ΔG0与K间的关系 ΔG0—标准自由焓 K—化学平衡常数 对于偏摩尔自由焓,它与活度存在有下列关系: i Gi = Gi i i RT ln a ˆ 0 + 前面已经讨论过,化学位与偏摩尔性质是两个独立的概念, 只有当 时,二者才为同一值。 = i i i G RT ln a ˆ 0 = + 式中: Gi 0— 组分i在标准态时的自由焓。 (10-11)

要注意化学平衡中的标准态与相平衡中所涉及的标准态不同, 标准态: 相平衡:与系统T、P相同时的纯组分 化学平衡:在系统T与固定压力(1atm)下的纯组分 将(10-11)式代入(10-10)式,得∑y,(G,°+RTna)=0 进行整理: ∑y,G,°+RT∑y,ha,=0 ∑y,ha=∑na=ha+ha,+.=n(aay)=hΠa" Λ 令K=Πa1 (10-13) AG°=∑yG
19 要注意化学平衡中的标准态与相平衡中所涉及的标准态不同, 标准态 : 相平衡:与系统T、P相同时的纯组分 化学平衡:在系统T与固定压力(1atm)下的纯组分 将(10-11)式代入(10-10)式,得 ( ln ) 0 0 + = i i i G RT ln ˆ 0 0 进行整理: i Gi + RT i ai = ∵ i i i i i i i i a a a a a a a ln ˆ ln ˆ ln ˆ ln ˆ . ln( ˆ .ˆ .) ln ˆ 1 2 = = 1 + 2 + = 1 2 = (10-13) i i a 0 0 i G = i G 令 K=

.△G+RTnK=0或 △G0=-RTnK (10-14) 标准态是固定压力1atm,△G=f(T) K=f(T) 注意点: (1) △G仅是T的函数, △Gf(T,P) 标准态下 反应体系 (2)平衡态处△G=0, 但△G不一定等于零 20
20 ∵ 标准态是固定压力1atm,△G 0=f(T) ln 0 0 G + RT K = G RT ln K 0 ∴ 或 = − (10-14) ∴ K=f(T) (2) 平衡态处 △G=0, 但△G 0 不一定等于零 注意点: (1) △G 0仅是T的函数, △G=f(T,P) 标准态下 反应体系