
§10.1一维非恒定流动的基本方程 一.连续方程 在管道中取出一段长度为 ds的控制体微元,n一n为 一◆ 上游断面,断面面积为A, 流速为口,液体密度为P, m一m为下游断面,坐标s与 -ds n 水流方向一致。 dt时段内通过n一n断面流入的液体质量为pAvdt 同一时段dt内通过m一m断面流出的液体质量为 pAvdt+pAvdtlds os
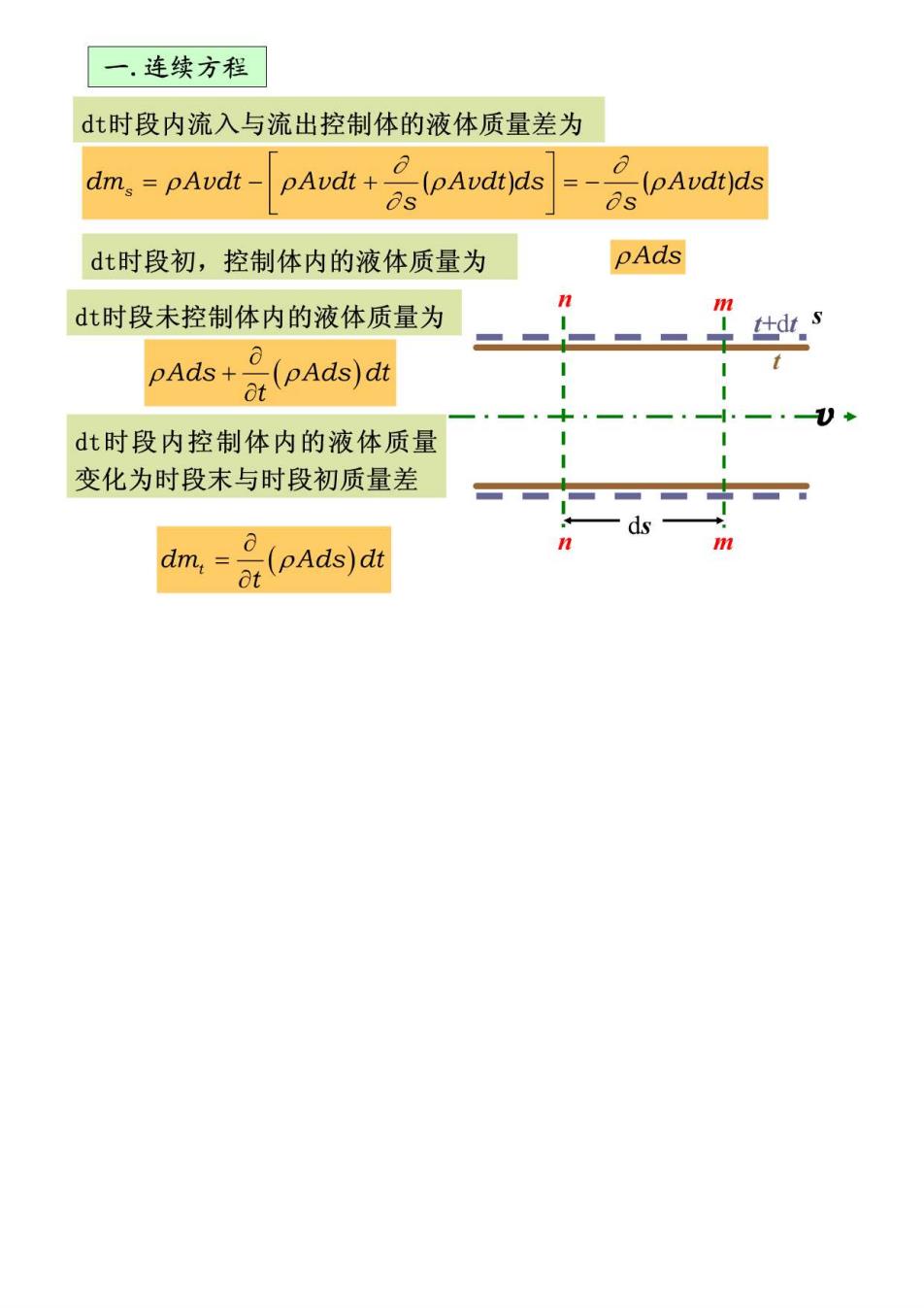
一.连续方程 dt时段内流入与流出控制体的液体质量差为 dm pAudt- pAvdt+(pAvdrds -(pAvdt)ds os o dt时段初,控制体内的液体质量为 pAds 11 dt时段未控制体内的液体质量为 pAds+(pAds)dt dt时段内控制体内的液体质量 变化为时段末与时段初质量差 dm, a(pAds)dt

根据质量守恒原理,在t时段内,流入与流出该控制体的液体 质量差应等于同一时段内该控制体内的质量变化,即 -(pvAdt)ds -(pAds)dt 或写成 is (DAU)+ (A 一维非恒定流的连续性方程 对不可压缩液体,即p=cost,但过水断面随时间变化,则上 式可简化为 (A)+ =0 at 对于既不考虑液体压缩性,也不考虑管壁材料的弹性,即断面大 小保持不变的管道非恒定流,上式可简化为 Av=Q=f(t) 对于不可压缩液体的恒定流运动 Av=Q=const

二,运动方程 应用牛顿第二运动定律,根据重力、压力、摩擦力和惯性力 的平衡,可直接写出处于渐变流段中长度为s的控制体微元的 液体运动方程 ds-roxas-pasf(+d=0 其中τo为流段管壁的平均切应 t+dt 力。忽略被积量在断面上的不 均匀影响,则可近似写成: +中+++-0 ds y ds g ot ds'rA

三.能量方程 运动方程 2+10++u0")+=0 as y ds'g o YA 对运动方程从断面s,至断面s,积分得 名++ =,+B++d+ods 2g y 2g g o YA 单位重量流体所受壁面摩擦力在断面s YA 至断面s,间所作的功,记为h12 17 h, ds 非恒定流动新增的水头,称为惯性水头