电子科技大学：《振动理论与声学原理 Vibration and Acoustics》课程教学资源（课件讲稿）第四章 多自由度系统的振动

一、多自由度系统的动力学方程一 作用力方程 建立方程： m花1+kx+k(x-x2)=P(t) 力量纲 m22-k2(x1-x2)+k3X2=P2(t) 写成矩阵形式： 0 坐标间的耦合项 11

11 建立方程： 1 1 1 1 2 1 2 1 2 2 2 1 2 3 2 2 ( ) ( ) ( ) ( ) m x k x k x x P t m x k x x k x P t              写成矩阵形式：                                     ( ) ( ) 0 0 2 1 2 1 2 2 3 1 2 2 2 1 2 1 P t P t x x k k k k k k x x m m   力量纲 坐标间的耦合项

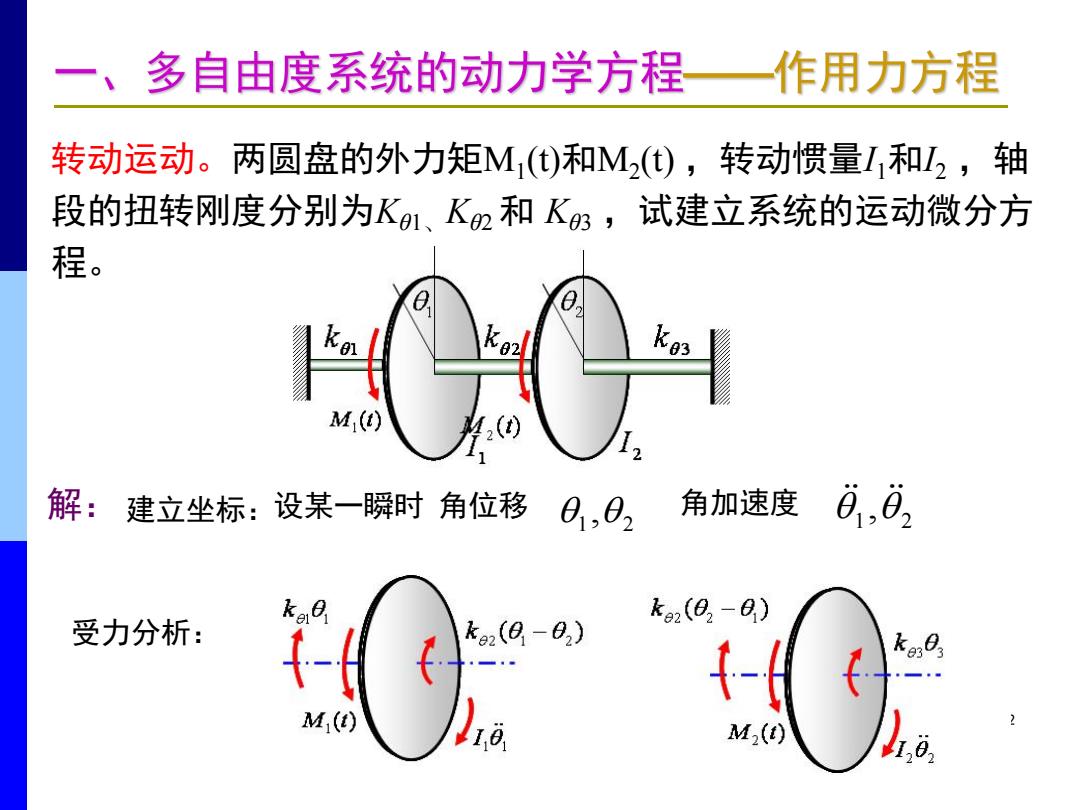
一、 多自由度系统的动力学方程— 作用力方程 转动运动。两圆盘的外力矩M()和M(),转动惯量I和2，轴 段的扭转刚度分别为K1、K2和K,试建立系统的运动微分方 程。 M,() 解：建立坐标：设某一瞬时角位移 0,02 角加速度 6,02 k2(82-8) 受力分析： ko2(0-02) - M1() M2()

12 转动运动。两圆盘的外力矩M1(t)和M2(t) ，转动惯量I1和I2 ，轴 段的扭转刚度分别为Kθ1、Kθ2和 Kθ3 ，试建立系统的运动微分方 程。 建立坐标： 角位移 1 2 设某一瞬时  , 角加速度 1 2  , 解：   受力分析：

一、多自由度系统的动力学方程— 作用力方程 kg2(8-8) 受力分析： k2(g-82) - M1(e) M2(t) 建立方程： I,8,+k01+k2(01-02)=M1() I202+k2(02-0)+k,03=M2(t) 写成矩阵形式： 6卧8 -k2 4 M2(t) 坐标间的耦合项 13

13 建立方程：             ( ) ( ) ( ) ( ) 2 2 2 2 3 3 2 1 1 1 1 2 1 2 1 1 I k k M t I k k M t              写成矩阵形式：                                    ( ) ( ) 0 0 2 1 2 1 2 2 3 1 2 2 2 1 2 1 M t M t k k k k k k I I             坐标间的耦合项 受力分析：

一、多自由度系统的动力学方程 作用力方程 小结： 6网 1、多自由度系统的角振动与直线振动在数学描述上相同。 2、如同在单自由度系统中做过的那样，在多自由度系统中也将质量、刚度、 位移、加速度及力都理解为广义的。可统一表示为： M X+K X=Pt 作用力方程 质量矩阵 加速度向量 刚度矩阵 位移向量 激励力向量 若系统有n个自由度，则各项 皆为n维 14

14 1、多自由度系统的角振动与直线振动在数学描述上相同。                                   ( ) ( ) 0 0 2 1 2 1 2 2 3 1 2 2 2 1 2 1 P t P t x x k k k k k k x x m m                                     ( ) ( ) 0 0 2 1 2 1 2 2 3 1 2 2 2 1 2 1 M t M t k k k k k k I I             小结: 2、如同在单自由度系统中做过的那样，在多自由度系统中也将质量、刚度、 位移、加速度及力都理解为广义的。可统一表示为： M X  K X  P(t)  作用力方程 位 移 向 量 加 速 度 向 量 质 量 矩 阵 刚 度 矩 阵 激 励 力 向 量 若系统有 n 个自由度，则各项 皆为 n 维

一、多自由度系统的动力学方程 刚度矩阵和质量矩阵 考察作用力方程： MX +KX=P(t X∈R” 当M、K确定后， 系统动九方程即可完全确定。那么M、K该如何确定？ 刚度矩阵K 假设外力是以准静恭式施加于系统，加速度为零。X=0 则： KX=P(t) 假设作用于系统的是这样一组外力，它们使系统只在第个坐标上产生 单位位移，而在其他各个坐标上不产生位移。即： X=[x1,,xj-1,Xj,xj+1,n]=[0,,0,100] 代入：KX=P(t) 15

15 当 M、K 确定后，系统动力方程即可完全确定。 那么 M、K 该如何确定？ MX  KX  P(t)  考察作用力方程： n X  R 刚度矩阵K 则： KX  P(t) 加速度为零。X  0 假设外力是以准静态方式施加于系统，  假设作用于系统的是这样一组外力，它们使系统只在第 j 个坐标上产生 单位位移，而在其他各个坐标上不产生位移。即： T T j j j n [x ,..., x , x , x ,..., x ] [0,...,0,1,0,...,0] X  1 1 1  代入 ： KX  P(t)