
4.1.1.节点电压方程的建立 系数Y(i≠j)称为节点i、j之间的 互导纳,其值等于连接这两个节点的 支路导纳的负值。 Y34=? 例如Y12=Y21=-y12, 若两节点之间不存在 Y35=? 直接连接的支路,则 1M2 45 有Y=0,例如 Y13=Y31=0。 ○0o
4.1.1.节点电压方程的建立 • 系数Yij( )称为节点i、j之间的 互导纳,其值等于连接这两个节点的 支路导纳的负值。 i j Y34=? Y35=? •例如Y12= Y21= -y12, •若两节点之间不存在 直接连接的支路,则 有Yij=0,例如 Y13=Y31=0
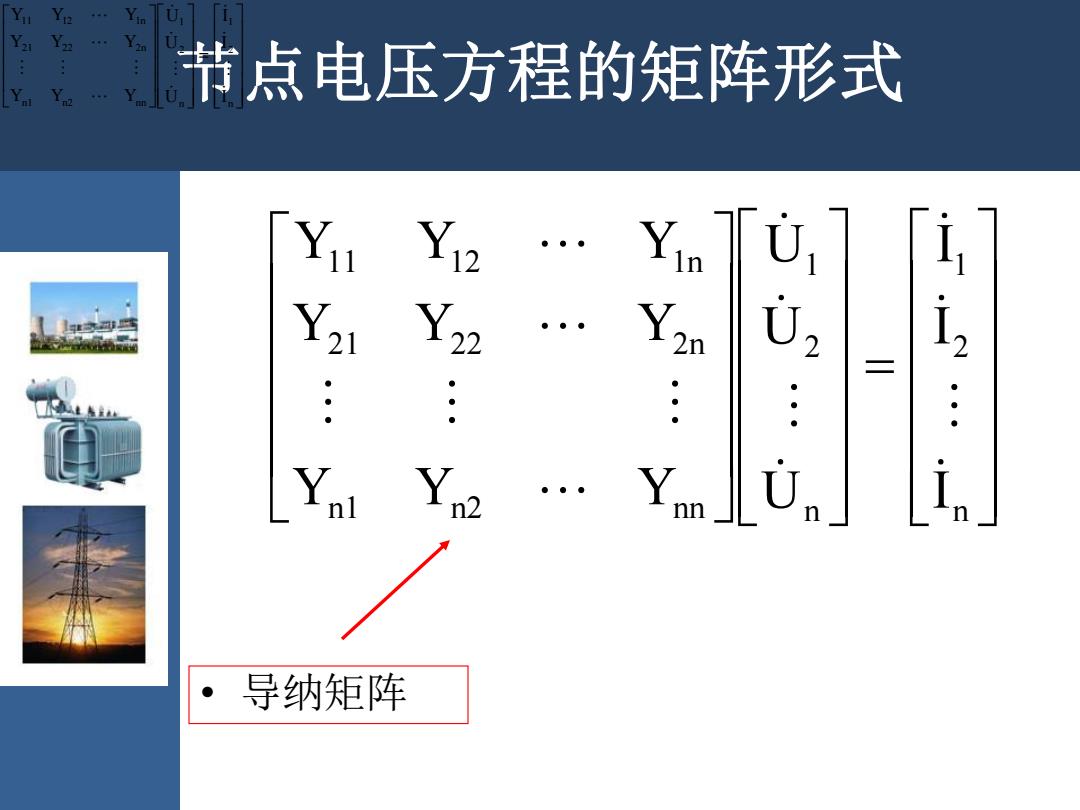
Y 节点电压方程的矩阵形式 11 义1n U Y21 02 二 ● : U i nl nn ·导纳矩阵
节点电压方程的矩阵形式 • 导纳矩阵 n 2 1 n 2 1 n1 n2 nn 21 22 2n 11 12 1n I I I U U U Y Y Y Y Y Y Y Y Y n 2 1 n 2 1 n1 n2 nn 21 22 2n 11 12 1n I I I U U U Y Y Y Y Y Y Y Y Y

4.1.2.节点导纳矩阵及其修正 导纳矩阵的特点: 1)电力网络中节点非常多,对有个节 点的电力网络而言,其导纳矩阵为一个 的方阵,且是对称矩阵,即有Yj=Yji。 2)其元素(导纳)是复数,所以是一个复 数矩阵 3)所有的对角元素为自导纳,为正值。 4)所有的非对角元素是两个相连接的节 点之间支路导纳的负值,当两节点不相 连接时,非对角元素为零
4.1.2.节点导纳矩阵及其修正 • 导纳矩阵的特点: • 1)电力网络中节点非常多,对有n个节 点的电力网络而言,其导纳矩阵为一个 的方阵,且是对称矩阵,即有Yij=Yji。 • 2)其元素(导纳)是复数,所以是一个复 数矩阵 • 3)所有的对角元素为自导纳,为正值。 • 4)所有的非对角元素是两个相连接的节 点之间支路导纳的负值,当两节点不相 连接时,非对角元素为零

4.1.2.节点导纳矩阵及其修正 ·求下图的导纳矩阵: 1、Y是几阶对称方阵? 2、Y44=? 21 Zn Y21 左 ZT2 5 3 Z☒ 宁2士2左g左Y3 YT2 G1 2
4.1.2.节点导纳矩阵及其修正 • 求下图的导纳矩阵: • 1、Y是几阶对称方阵? • 2、Y44=?
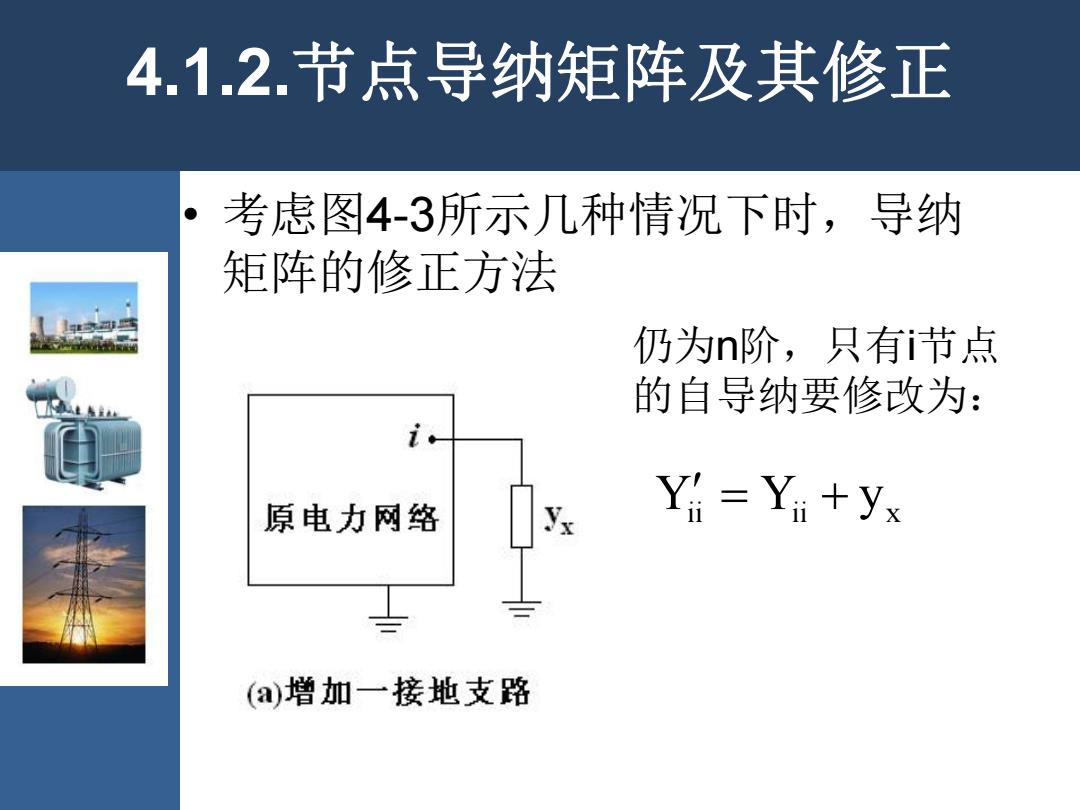
4.1.2.节点导纳矩阵及其修正 考虑图4-3所示几种情况下时,导纳 矩阵的修正方法 仍为n阶,只有i节点 的自导纳要修改为: 原电力网络 Yi=Yi+yx (a增加一接地支路
4.1.2.节点导纳矩阵及其修正 • 考虑图4-3所示几种情况下时,导纳 矩阵的修正方法 仍为n阶,只有i节点 的自导纳要修改为: Yii Yii yx