
静电场 Xidian University 例:平径为a的球形空间内均匀分布有电荷体密度为p的电荷, 试求静电场能量。 解:方法-,利用R=灯Dd 根据高斯定理求得电场强度 , E,= (r<a) E2=e, 8r2 (r>a) 故 成-J,D-ar=d+引dv 4π 156 西安电子科技大学
西安电子科技大学 例:半径为a 的球形空间内均匀分布有电荷体密度为ρ的电荷, 试求静电场能量。 2 2 2 6 2 2 2 5 0 2 2 4 0 0 0 0 1 4 ( 4 d 4 d ) 2 9 9 15 a a r a r r r r a r 1 0 ( ) 3 r r E e r a 解: 方法一,利用 1 d 2 e V W D E V 根据高斯定理求得电场强度 3 2 2 0 ( ) 3 r a E e r a r 故 1 2 2 2 0 1 0 2 1 1 1 d d d 2 2 2 e V V V W D E V E V E V 静电场

Xidian University 静电场 方法二:利用=,r 先求出电位分布 4=2d=小 (r≤a) 政-r-32u-5a 4πp2a 1560 西安电子科技大学
西安电子科技大学 3 1 1 2 2 0 0 2 2 0 d d d d 3 3 ( ) ( ) 2 3 a a r a r a r a E r E r r r r r a r a 方法二:利用 1 d 2 e V W V 先求出电位分布 故 2 2 2 2 2 5 1 0 0 0 1 1 4 d ( )4 d 2 2 2 3 15 a e V r W V a r r a 静电场

Xidian University 静电场 §2.2静电场的唯一性定理 上节回答了一般情况下如何求解p(), 基于微分方程和边值关系 本节要回答什么条件下,可唯一确定(), 唯一性定理 边值问题: 在给定的边界条件下,求解势函数的泊松方程或拉普拉斯方程 边值问题的类型: 第一类边值问题 已知场域边界面上的势函数值,即ps=(S) 第二类边值问题 已知场域边界面上的势函数的法向导数值,即吧-(S) On 西安电子科技大学
西安电子科技大学 § 2.2 静电场的唯一性定理 边值问题的类型: 1 | ( ) S 已知场域边界面上的势函数值,即 f S 2 | ( ) S f S n 边值问题: 在给定的边界条件下,求解势函数的泊松方程或拉普拉斯方程 第一类边值问题 已知场域边界面上的势函数的法向导数值,即 第二类边值问题 静电场

Xidian University 静电场 一、泊松方程和边界条件 假定所研究的区域为V,在一般情况下V内可以有多种介质 或导体,对于每一种介质自身是均匀线性各向同性。 设V内所求电势为P,它们满足泊松方程 (i=1,2,…,m) 两类边界条件: E ① 边界S上, 为已知,若为导体p、=常数。 ② 边界S上, ap 为已知,若是导体要给定总电荷Q。 它相当于 on\s 给定(0=4. ds 西安电子科技大学
西安电子科技大学 2 ( 1,2, , ) i i i m 一、泊松方程和边界条件 假定所研究的区域为V,在一般情况下V内可以有多种介质 或导体,对于每一种介质自身是均匀线性各向同性。 设V内所求电势为 i ,它们满足泊松方程 S n S n S S S Q dS n S 两类边界条件: 为已知,若为导体 =常数。 为已知, 它相当于 给定( ) 若是导体要给定总电荷Q。 ① 边界S上, ② 边界S上, 静电场
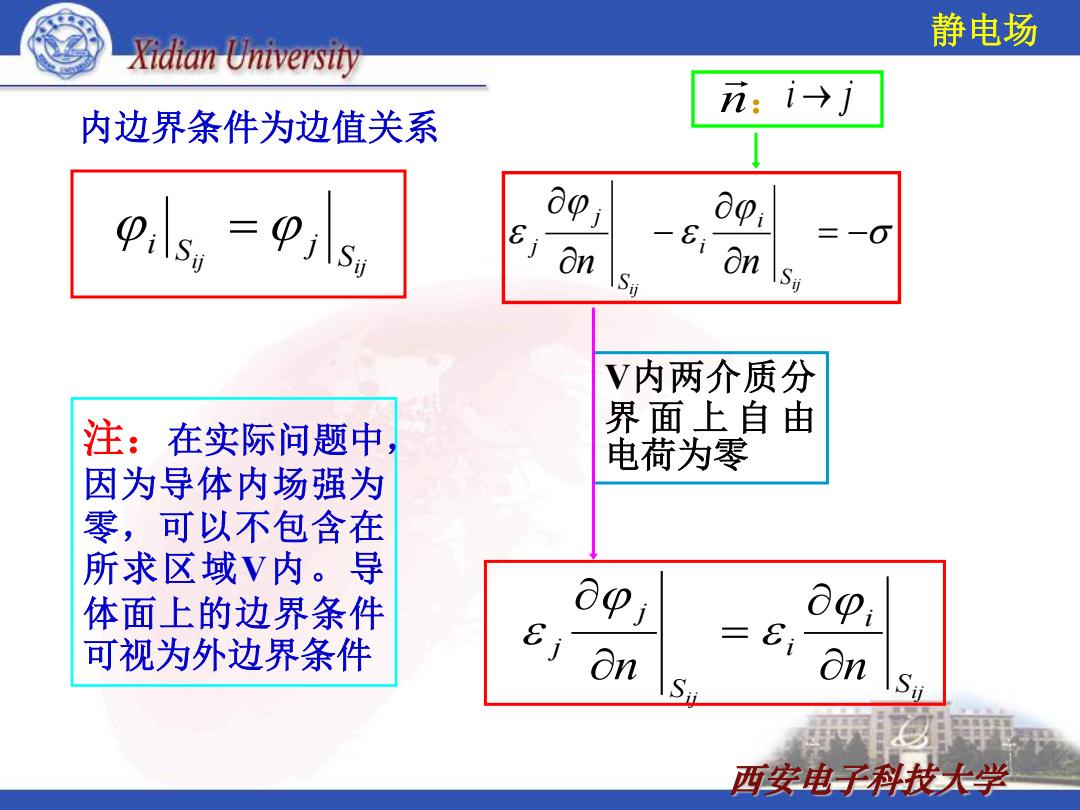
Xidian University 静电场 n:i→j 内边界条件为边值关系 o0j 001 On On V内两介质分 注:在实际问题中 界面上自由 电荷为零 因为导体内场强为 零,可以不包含在 所求区域V内。导 体面上的边界条件 00j 001 可视为外边界条件 &i 二i On On Si 西安电子科技大学
西安电子科技大学 ij ij S i i S j j n n 内边界条件为边值关系 注:在实际问题中, 因为导体内场强为 零,可以不包含在 所求区域V内。导 体面上的边界条件 可视为外边界条件 ij ij S i S j ij ij S i i S j j n n n : i j V内两介质分 界 面 上 自 由 电荷为零 静电场