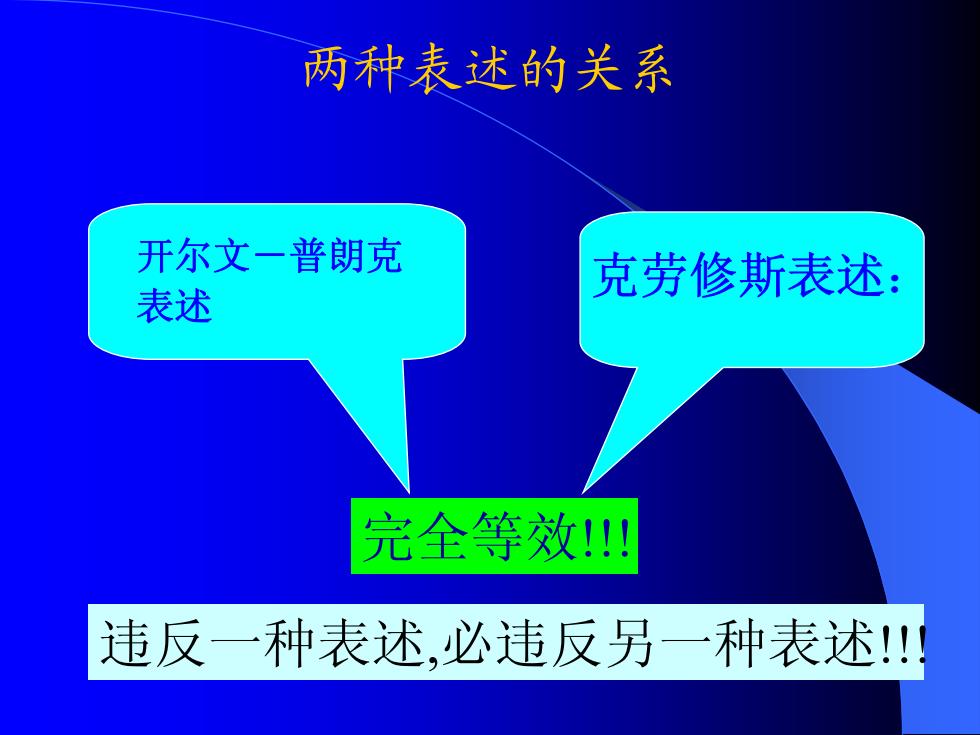
两种表述的关系 开尔文一普朗克 克劳修斯表述: 表述 完全等效! 违反一种表述,必违反另一种表述!
两种表述的关系 开尔文-普朗克 表述 完全等效!!! 克劳修斯表述 : 违反一种表述 ,必违反另一种表述!!!

Spontaneous process exists direction, condition and bounds. 22 How much can the thermal efficiency achieve? What influence the thermal efficiency?
Spontaneous process exists direction, condition and bounds. How much can the thermal efficiency achieve? What influence the thermal efficiency?
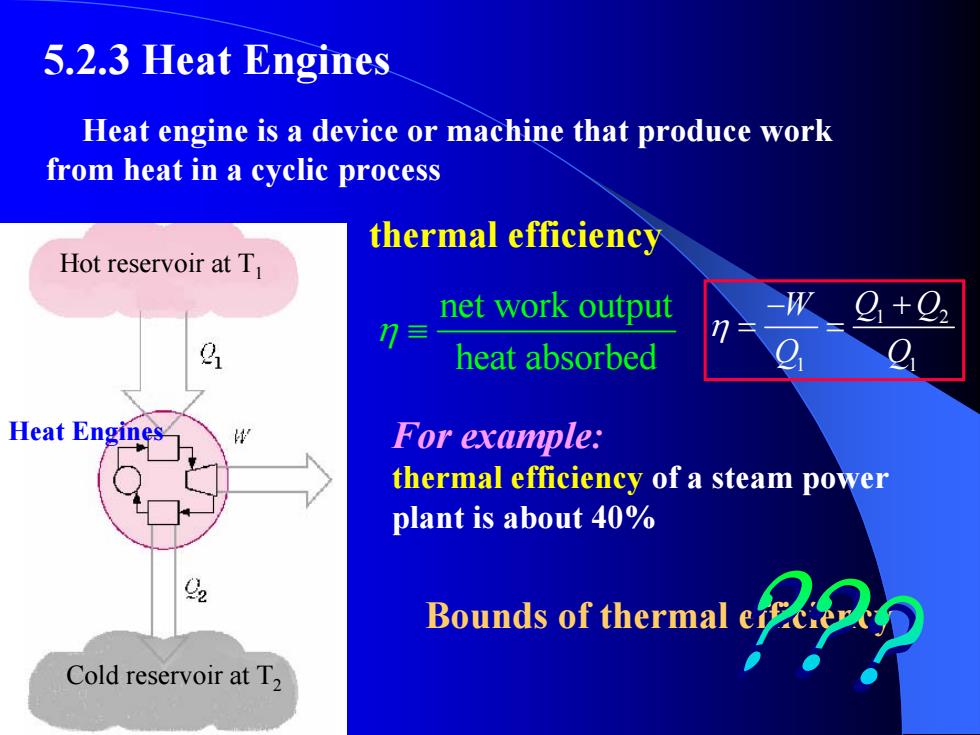
5.2.3 Heat Engines Heat engine is a device or machine that produce work from heat in a cyclic process thermal efficiency Hot reservoir at T net work output heat absorbed Heat Engines For example: thermal efficiency of a steam power plant is about 40% Bounds of thermal Cold reservoir at T2
For example: thermal efficiency of a steam power plant is about 40% 1 2 1 1 W Q Q Q Q η − + = = Hot reservoir at T1 Cold reservoir at T2 Heat Engines Heat engine is a device or machine that produce work from heat in a cyclic process thermal efficiency Bounds of thermal efficiency 5.2.3 Heat Engines net work output heat absorbed η ≡

5.2.4 Carnot's Theorem For two given heat reservoirs no engine can have a thermal efficiency higher than that of a Carnot engine.The thermal efficiency of a Carnot engine depends only on the temperature levels and not upon the working substance of the engine. Carnot efficiency -W 7= =1- T For two given heat reservoirs no engine can have a thermal efficiency higher than that of a Carnot engine. T
5.2.4 Carnot’s Theorem : For two given heat reservoirs no engine can have a thermal efficiency higher than that of a Carnot engine. The thermal efficiency of a Carnot engine depends only on the temperature levels and not upon the working substance of the engine. T1 T2 Rc Q1 Q2 W Carnot efficiency For two given heat reservoirs no engine can have a thermal efficiency higher than that of a Carnot engine. 1 2 1 1 T T Q W −= − η =

5.3 Entropy and Entropy Change 5.3.1 Entropy and theorem of entropy increasing This mathematical statement of the second law affirms that every proceeds in such a direction that the total entropy change associated with it is positive,the limiting value of zero being attained only by a reversible process.No process is possible for which the total entropy decreases. s≥ T for isolated system The entropy of an isolated system during a process always dS≥0 increase or,in the limiting case of a reversible process,remains theorem of entropy increasing constant
5.3 Entropy and Entropy Change 5.3.1 Entropy and theorem of entropy increasing T Q dS δ ≥ This mathematical statement of the second law affirms that every proceeds in such a direction that the total entropy change associated with it is positive, the limiting value of zero being attained only by a reversible process. No process is possible for which the total entropy decreases. dS ≥ 0 for isolated system theorem of entropy increasing The entropy of an isolated system during a process always increase or, in the limiting case of a reversible process, remains constant