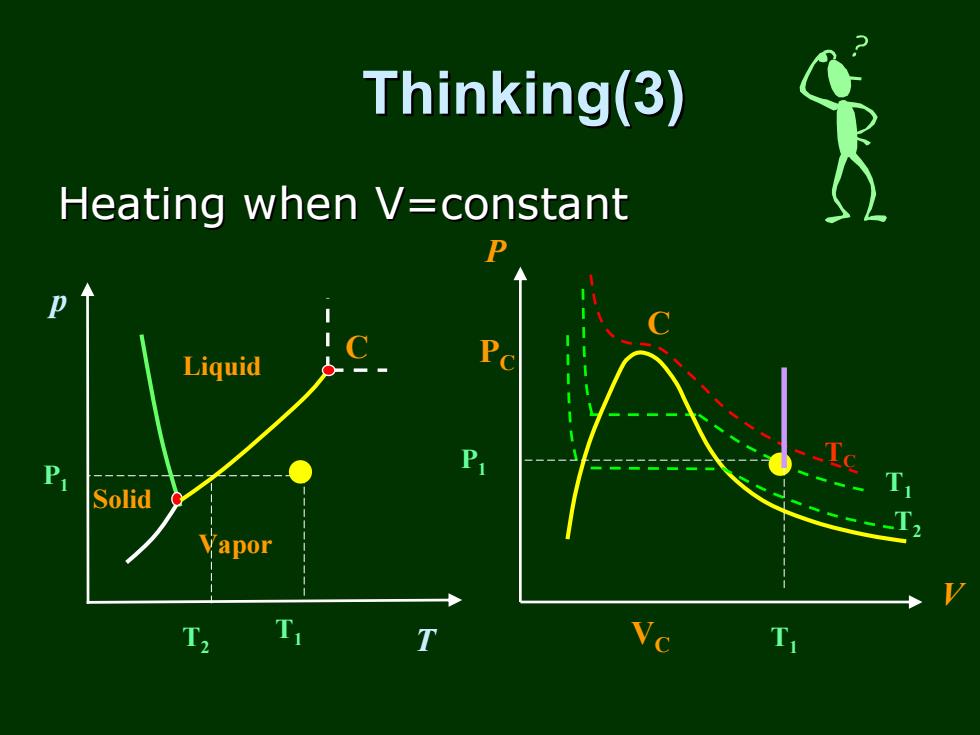
Thinking(3) Heating when V=constant 力 Liquid P Solid Vapor T T T
p T Liquid Vapor Solid C Thinking(3) Thinking(3) T1 P1 PC T1 P VC V TC C T2 T2 T1 P1 Heating when V=constant Heating when V=constant

3.2 Virial Equations of state For a pure substance Fmax=C-P+2=1-1+2-=2 that is:For a pure substance,fixing two of its properties fixes all the others,and thus determines its thermonadymic state. We can write T=o(P,V)or P=v(T,V)or V=5(P,T) f(P,V,T)=0 The equation of state (EOS)
3.2 Virial Equations of state 3.2 Virial Equations of state that is: For a pure substance, fixing two of its properties fixes all the others, and thus determines its thermonadymic state. For a pure substance Fmax = ? Fmax =C-P+2=1-1+2=2 T P V or P T V or V P T = ϕ(, ) (, ) (,) = = ψ ζ The equation of state (EOS) f PV T (,) 0 = We can write

The necessary conditions of EOS 1)According with critical condition 2)P→0(→∞),according with the law of ideal gas EOS的价值: 1)精确地代表相当广泛范围内的PVT数据,大 大减少实验测定工作量。 2)可直接计算不做实验测定的其它热力学性质 3)进行相平衡的计算 但其通用性差,要在广泛的气体密度范围内 即用于极性物质,又用于非极性物质,又要精 度,很难做到
The necessary conditions of EOS The necessary conditions of EOS 1 )According with critical condition According with critical condition 2 ) P → 0 ( V→∞ ), according with the law , according with the law of ideal gas of ideal gas EOS的价值 : 1)精确地代表相当广泛范围内的 )精确地代表相当广泛范围内的PVT数据,大 大减少实验测定工作量。 大减少实验测定工作量。 2)可直接计算不做实验测定的其它热力学性质 )可直接计算不做实验测定的其它热力学性质 3)进行相平衡的计算 )进行相平衡的计算 但其通用性差,要在广泛的气体密度范围内 但其通用性差,要在广泛的气体密度范围内 即用于极性物质, 即用于极性物质,又用于非极性物质,又要精 又用于非极性物质,又要精 度,很难做到

Two forms of the Virial Equation Compressibility factor PV C-. C-B2 RT (RT Z=1+BP+CP2+DP3+- B RT B C D or Z=1++六++. D'=D-3BC+2B (RT) B is second virial coefficients; C is third virial coefficients;etc. For a given gas, the virial coefficients are functions of temperature only
Two forms of the Virial Equation Two forms of the Virial Equation P V Z RT ≡ Compressibility factor ' '2 '3 Z BP CP DP =+ + + + 1 ┅ 2 3 1 BC D Z VV V =+ + + + ┅ ' B B R T = ( ) 2 ' 2 C B C RT − = ( ) 3 ' 3 D 3 2 BC B D RT − + = or B is second virial coefficients; C is third virial coefficients; etc. For a given gas, the virial coefficients are functions of temperature only

The Virial equation is the only one having a firm basis in theory. The methods of statistical mechanics allow derivation of the virial equation and provide physical significance to the Virial coefficients. For the expansion in 1/V B Z=1+ V23 十 the term B/V-interactions between paris of molecules the term C/V2-three-body interactions,etc
The Virial equation is the only one having a firm The Virial equation is the only one having a firm basis in theory. basis in theory. The methods of statistical mechanics allow The methods of statistical mechanics allow derivation of the virial equation and provide physical derivation of the virial equation and provide physical significance to the Virial coefficients. significance to the Virial coefficients. the term B/V the term B/V ——interactions between paris of interactions between paris of molecules molecules the term C/V the term C/V2——three -body interactions, etc. body interactions, etc. For the expansion in 1/V For the expansion in 1/V 2 3 1 BC D Z VV V = ++ + + ┅