
ux=u(x,y,z,t) uy =uy(x,y,z,t) u:=u=(x,y,z,t) 若令上式中x、y、z为常数,t为变 数,即可求得在某一固定空间点上液体 质点在不同时刻通过该点的流速的变化 情况。 若令t为常数,x、y、z为变数,则 可求得在同一时刻,通过不同空间点 上的液体质点的流速的分布情况(即流 速场)
着眼于运动液体的质 点,跟踪质点描述其运 拉格朗日法 眼踪 动历程 拉格朗日法必须建立质点运动坐标的函数关系式,这在数学处理上 将十分困难,除研究如射流、波浪运动等流动问题外很少采用 欧拉法 着眼于空间点,研究质 布峭 点流经空间各固定点的 运动特性 欧拉法以数学中的场论为基础,着眼于任何时刻物理量在流场 中的分布规律。因此水力学研究液体运动普遍采用欧拉法

3.2液体运动的基本概念(欧拉法) •恒定流与非恒定流 •迹线与流线 •流管、微小流來、总流和过水断面 •流量和断面平均流速 •水流的分类 ·均匀流、渐变流过水断面的重耍特性
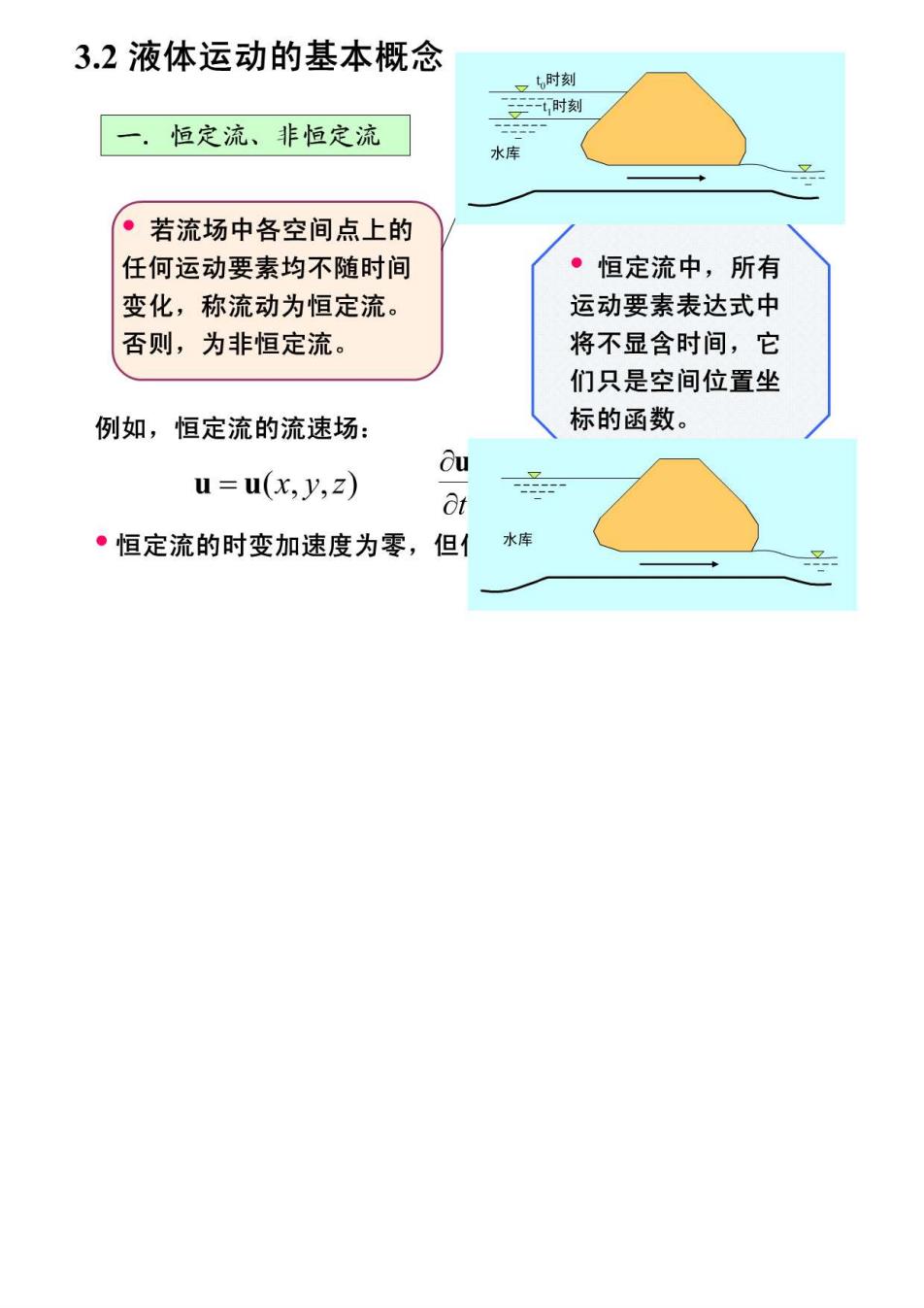
3.2液体运动的基本概念 时刻 时刻 一·恒定流、非恒定流 水库 。若流场中各空间点上的 任何运动要素均不随时间 ·恒定流中,所有 变化,称流动为恒定流。 运动要素表达式中 否则,为非恒定流。 将不显含时间,它 们只是空间位置坐 例如,恒定流的流速场: 标的函数。 Cu u=u(x,y,z) ·恒定流的时变加速度为零,但 水库

二.迹线与流线 迹线的定义 迹线(Path Line) 某一质点在某一 内的运动轨迹线。 就是指某液体质 运动过程中,不 刻所流经的空间点 连成的线