N缝衍射的振幅和强度分布 BN ae 00 ae单缝衍射图样 2NB BN △ sin a ae πa ae X= sin a 缝间(相邻衍射单元)光程差: 1®B △L=dsin 0 ao B 缝间(相邻衍射单元)位相差:δ=2B=kAL= 2πd sine
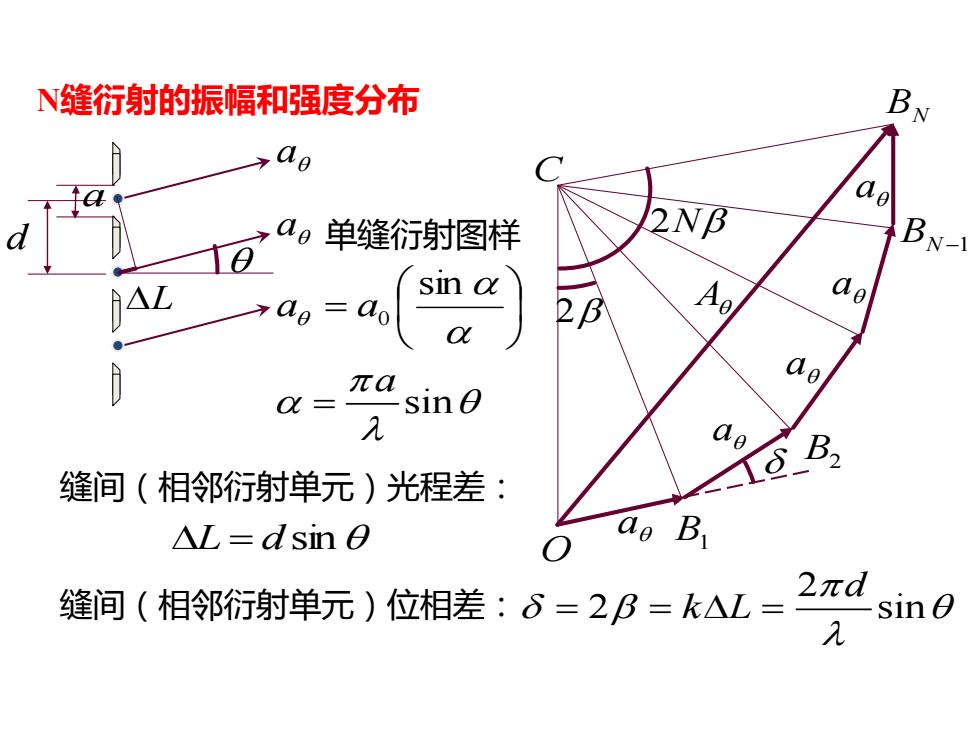
N缝衍射的振幅和强度分布 缝间(相邻衍射单元)光程差: 缝间(相邻衍射单元)位相差: L = d sin 2 2 sin d k L = = = L d a a a a a a a C O B1 B2 BN−1 BN 2 A 2N = sin a a0 sin a = a 单缝衍射图样

BN N缝行射的振幅和强度分布 a NB BN OB=Ap=20Csin NB ag 2sin6→4。=ag sin NB ae OC= sin B 16B ao B 1=46=a sin sin NB a 其中: sin B a=. Ta sin 0 单缝衍射因子 缝间干涉因子 B= πd (单元因子) (N元干涉因子) -sin 0 说明:在光栅的缝宽和缝间距一定的情况下,干涉的光强结果和 波长以及角度有关,这也就决定了相同波长的单色光在不同角度 下,干涉所得的光强不同;不同波长的光在相同角度下,干涉所 得的光强也不同
N缝衍射的振幅和强度分布 sin sin N A = a 其中: sin a = sin d = 单缝衍射因子 (单元因子) 缝间干涉因子 (N元干涉因子) 2 2 2 2 0 sin sin sin N I A a = = OB A OC N N = = 2 sin a a a a a C O B1 B2 BN−1 BN 2 A 2N 说明:在光栅的缝宽和缝间距一定的情况下,干涉的光强结果和 波长以及角度有关,这也就决定了相同波长的单色光在不同角度 下,干涉所得的光强不同;不同波长的光在相同角度下,干涉所 得的光强也不同。 2sin a OC =
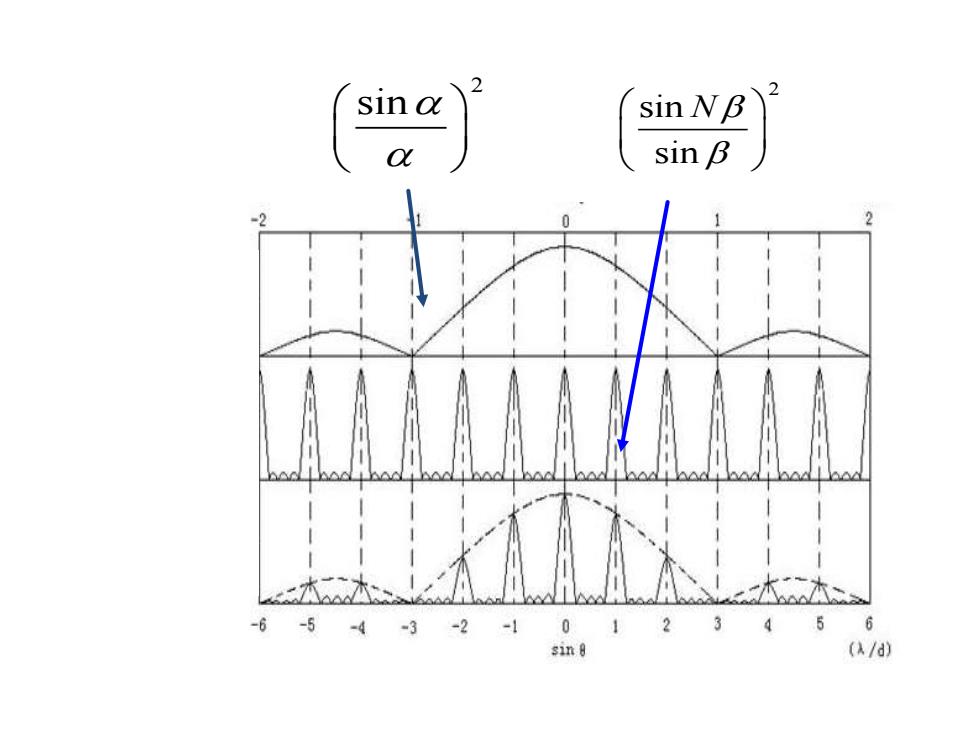
sin NB sin 0 6 (a/d)
2 sin 2 sin sin N

缝间干涉因子的特点 sin NB B= sin 0 (1)主极大: sin B ①位置 B-Jr→sim0=j话 j=0,±1,2,.,±n ②数目 jmax=[d/a] (sin0<1) ③强度 SinNB=N sin B 1Um)=1,(3naN2 单缝的NP倍 说明:主极大的强度与N有关,位置与N无关
缝间干涉因子的特点 ① 位置 sin j d = j n = 0, 1, 2, , ② 数目 j d max = ③ 强度 单缝的 N2 倍 (1)主极大: (sin 1) 说明:主极大的强度与N 有关,位置与N 无关 sin sin N N = = j 2 2 0 sin I j I N ( ) ( ) = 2 sin sin N sin d =

缝间干涉因子的特点 (2)零点和次级大: 干涉因子极小值 sinNB=0→NB=mnB≠nm sin B sin0=m2/Nd,sin0≠nλ/d sin=[0],A/Nd,.(N-1)A/Nd,[a/d], (N+1)z/Wd,(W+2)z/Nd,.(2N-1)2/Nd,[2/dl,. 零点: 位益sm9=(+)月 j=0,±1,±2,.,±n m=1,2,.2w21 个数:N1(两个主极大之间) 次极大:每两个相邻暗线之间存在一个次级大,共N-2个 (两个主极大之间)
缝间干涉因子的特点 (2)零点和次级大: 位置 sin m j N d = + 0, 1, 2, , 1,2, , 1 j n m N = = − 零点: 次极大:每两个相邻暗线之间存在一个次级大,共N-2个 (两个主极大之间)。 sin 0 , / , ( 1) / , / , ( 1) / ,( 2) / , (2 1) / , 2 / , Nd N Nd d N Nd N Nd N Nd d = − + + − 干涉因子极小值 sin / , sin / = m Nd n d sin 0 sin N = N m = n 个数:N-1(两个主极大之间)