
第十四章动态电路的频域分析 动态电路的基本分析方法是建立电路的微分方程 并求解微分方程得到电压电流,对于高阶动态电路而言 建立和求解微分方程都十分困难。对于单一频率正弦激 励的线性时不变电路,为避免建立和求解微分方程,常 常采用相量法。相量法是将正弦电压电流用相应的相量 电压电流表示,将电路的微分方程变换为复数代数方程 来求解,得到相量形式的电压电流后,再反变换为正弦 电压电流
第十四章 动态电路的频域分析 动态电路的基本分析方法是建立电路的微分方程, 并求解微分方程得到电压电流,对于高阶动态电路而言, 建立和求解微分方程都十分困难。对于单一频率正弦激 励的线性时不变电路,为避免建立和求解微分方程,常 常采用相量法。相量法是将正弦电压电流用相应的相量 电压电流表示,将电路的微分方程变换为复数代数方程 来求解,得到相量形式的电压电流后,再反变换为正弦 电压电流
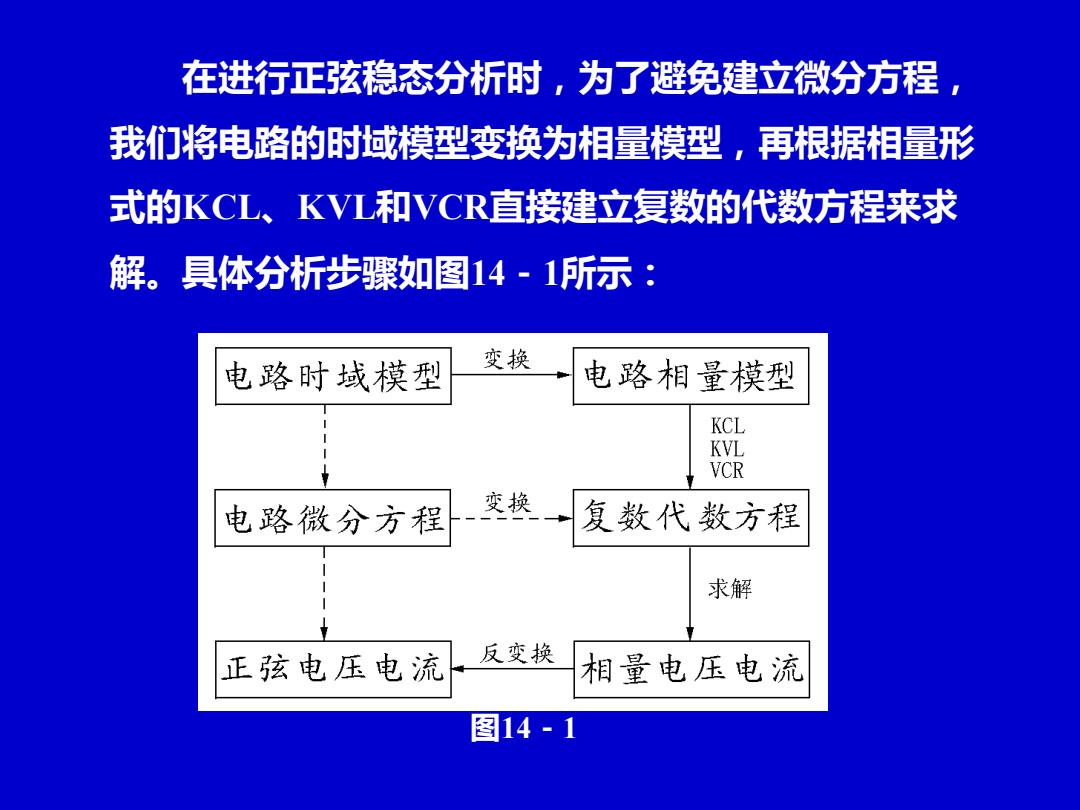
在进行正弦稳态分析时,为了避免建立微分方程 我们将电路的时域模型变换为相量模型,再根据相量形 式的KCL、KVL和VCR直接建立复数的代数方程来求 解。具体分析步骤如图14-1所示: 电路时域模型 变换 电路相量模型 KCL KVL VCR 电路微分方程 变换 复数代数方程 求解 正弦电压电流 反变换 相量电压电流 图14-1
在进行正弦稳态分析时,为了避免建立微分方程, 我们将电路的时域模型变换为相量模型,再根据相量形 式的KCL、KVL和VCR直接建立复数的代数方程来求 解。具体分析步骤如图14-1所示: 图14-1
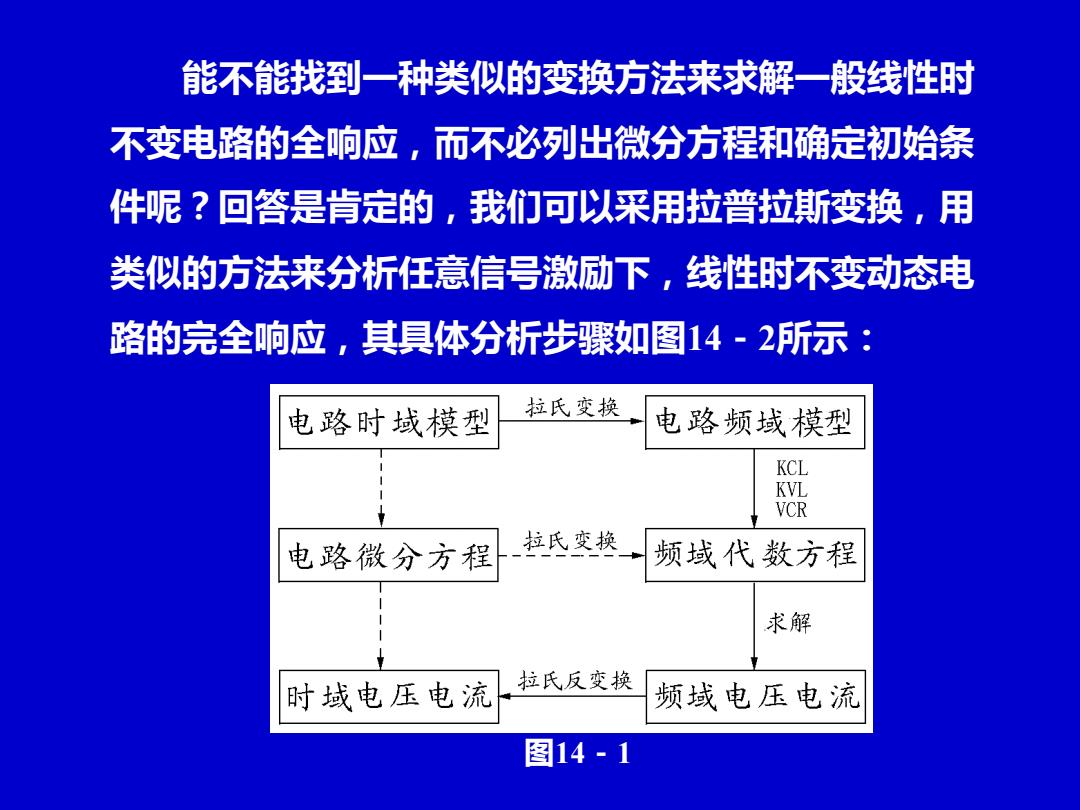
能不能找到一种类似的变换方法来求解一般线性时 不变电路的全响应,而不必列出微分方程和确定初始条 件呢?回答是肯定的,我们可以采用拉普拉斯变换,用 类似的方法来分析任意信号激励下,线性时不变动态电 路的完全响应,其具体分析步骤如图14-2所示 电路时域模型 拉氏变换 电路频域模型 KCL KVL VCR 电路微分方程 拉氏变换 频域代数方程 求解 时域电压电流 拉氏反变换 频域电压电流 图14-1
能不能找到一种类似的变换方法来求解一般线性时 不变电路的全响应,而不必列出微分方程和确定初始条 件呢?回答是肯定的,我们可以采用拉普拉斯变换,用 类似的方法来分析任意信号激励下,线性时不变动态电 路的完全响应,其具体分析步骤如图14-2所示: 图14-1
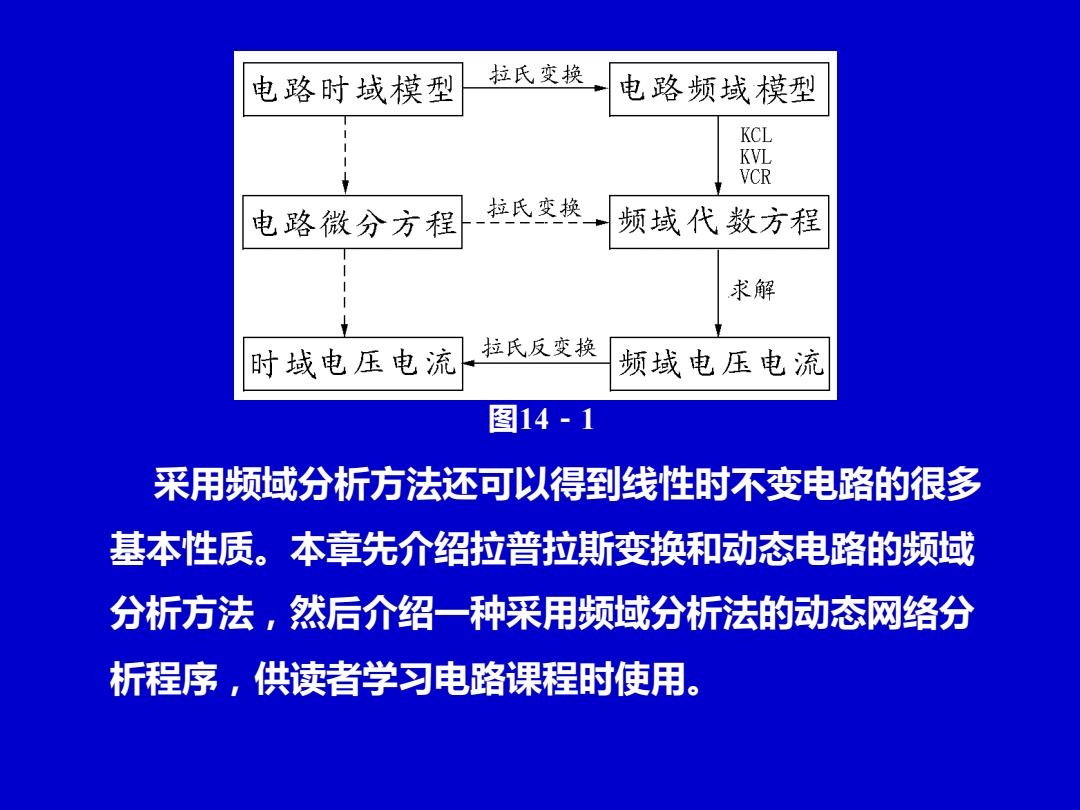
电路时域模型 拉氏变换 电路频域模型 KCL KVL VCR 电路微分方程 拉氏变换 频域代数方程 求解 时域电压电流 拉氏反变换 频域电压电流 图14-1 采用频域分析方法还可以得到线性时不变电路的很多 基本性质。本章先介绍拉普拉斯变换和动态电路的频域 分析方法,然后介绍一种采用频域分析法的动态网络分 析程序,供读者学习电路课程时使用
图14-1 采用频域分析方法还可以得到线性时不变电路的很多 基本性质。本章先介绍拉普拉斯变换和动态电路的频域 分析方法,然后介绍一种采用频域分析法的动态网络分 析程序,供读者学习电路课程时使用

§14-1拉普拉斯变换 时间函数f)的拉普拉斯变换记为L【f其定义为 Llf=∫rfe“d 其中S=σ称物复频率。积分的上下限是固定的,积分 的结果与无关,只取决于参数5,它是复频率的函数, 即 L f(t]=F(s) 在电路分析中,将时域的电压4()和电流()的拉普 拉斯变换记为U(s)和(s)
§14-l 拉普拉斯变换 − − = 0 [ f (t)] f (t)e dt s t L 时间函数f(t)的拉普拉斯变换记为 L [ f ,其定义为 (t)] L [ f (t)] = F(s) 其中 称为复频率。积分的上下限是固定的,积分 的结果与t无关,只取决于参数s,它是复频率的函数, 即 s = + j 在电路分析中,将时域的电压u(t)和电流i(t)的拉普 拉斯变换记为U(s)和I(s)