电子科技大学：《振动理论与声学原理 Vibration and Acoustics》课程教学资源（课件讲稿）第六章 线性振动的近似计算方法

一、邓克利法 (-1)”(2”+a,2”-+…+an-2+an)=0 a1=-(d1+d22+…+dnm)=-trD D=FM 当M为对角阵时： trD=tr(FM）=∑Jfnm, i= 特征方程又可写为： (2-2)(2-元2)…(2-2n)=0 有： a=-2A=-D=-2m 得： 2A=2fm】 。-2m i=1 i- 柔度系数的物理意义：沿第个坐标施加单位力时所产生的第个坐标的位移 kllfi

ki=1/fii ( 1) ( ) 0 1 1 1   1       n n n n n  a   a  a a1  (d11  d22  dnn )  trD 当 M 为对角阵时： trD  tr(FM) 特征方程又可写为： (  1 )(  2 )(  n )  0    n i i a 1 有： 1  得：      n i ii i n i i f m 1 1       n i ii i n i i f m 1 1 2 1  D=FM   n i iimi f 1  trD    n i iimi f 1 柔度系数 fii的物理意义：沿第i个坐标施加单位力时所产生的第i个坐标的位移

一、邓克利法 i=1 立m 如果只保留第i个质量，记所得的单自由度系统的固有频率为： k= m」 2m 将可代入： 对于梁结构系统，第二阶及第二阶以上的固有频率通常远大于基频， 因此左端可只保留基频项，有： 邓克利法 i=l

     n i ii i n i i f m 1 1  如果只保留第 i 个质量，记所得的单自由度系统的固有频率为： i ii i i i m f m 2 k 1         n i ii i n i i f m 1 1 2 1  将 i 2代入： 2 2 2 2 1 1 2 1 1 1 1 n n i i           对于梁结构系统，第二阶及第二阶以上的固有频率通常远大于基频， 因此左端可只保留基频项，有： 2 2 2 2 1 1 2 1 1 1 1 1 ( ) n ii i n i f m tr FM            邓克利法

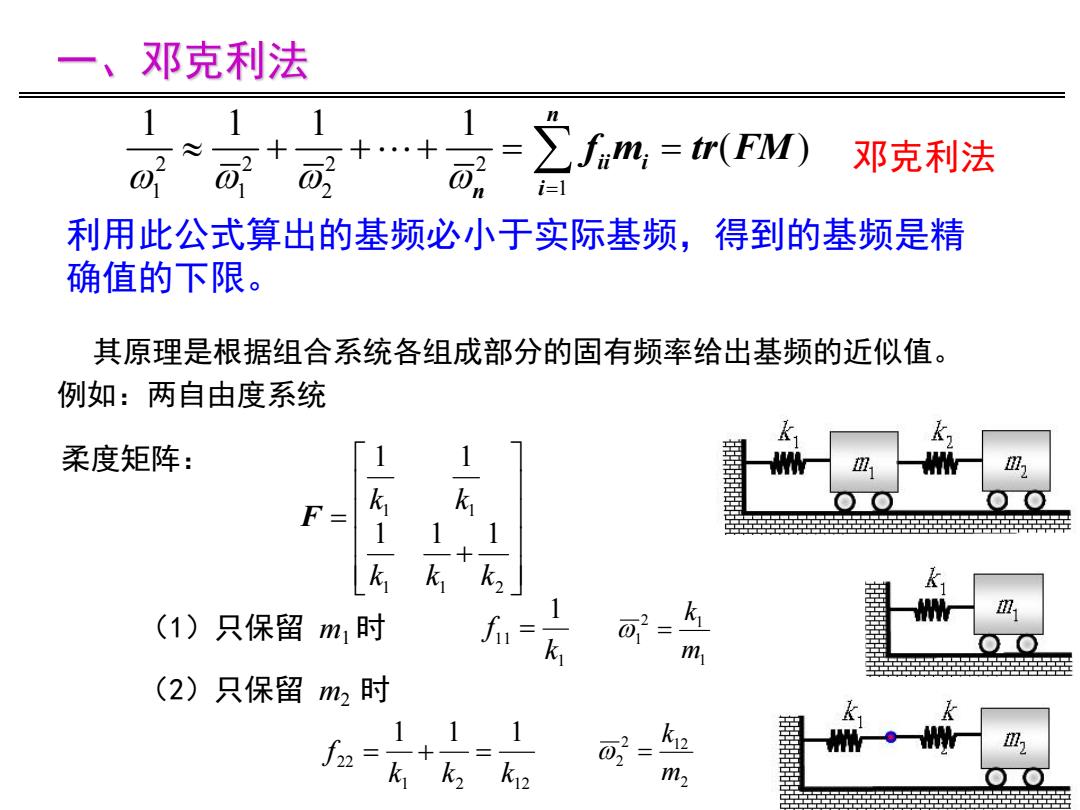
一、邓克利法 1 1 + 邓克利法 i=l 利用此公式算出的基频必小于实际基频，得到的基频是精 确值的下限。 其原理是根据组合系统各组成部分的固有频率给出基频的近似值。 例如：两自由度系统 柔度矩阵： 1 F= k k 1 1 k k (1)只保留m1时 fu m (2)只保留 m2时 111 业 k12 m2

柔度矩阵：         1 1 2 1 1 1 1 1 1 1 k k k k k F 例如：两自由度系统 1 11 1 k f  1 2 1 1 m k （1）只保留 m1时   1 2 12 22 1 1 1 k k k f    2 2 12 2 m k   （2）只保留 m2 时 2 2 2 2 1 1 2 1 1 1 1 1 ( ) n ii i n i f m tr FM            邓克利法 利用此公式算出的基频必小于实际基频，得到的基频是精 确值的下限。 其原理是根据组合系统各组成部分的固有频率给出基频的近似值

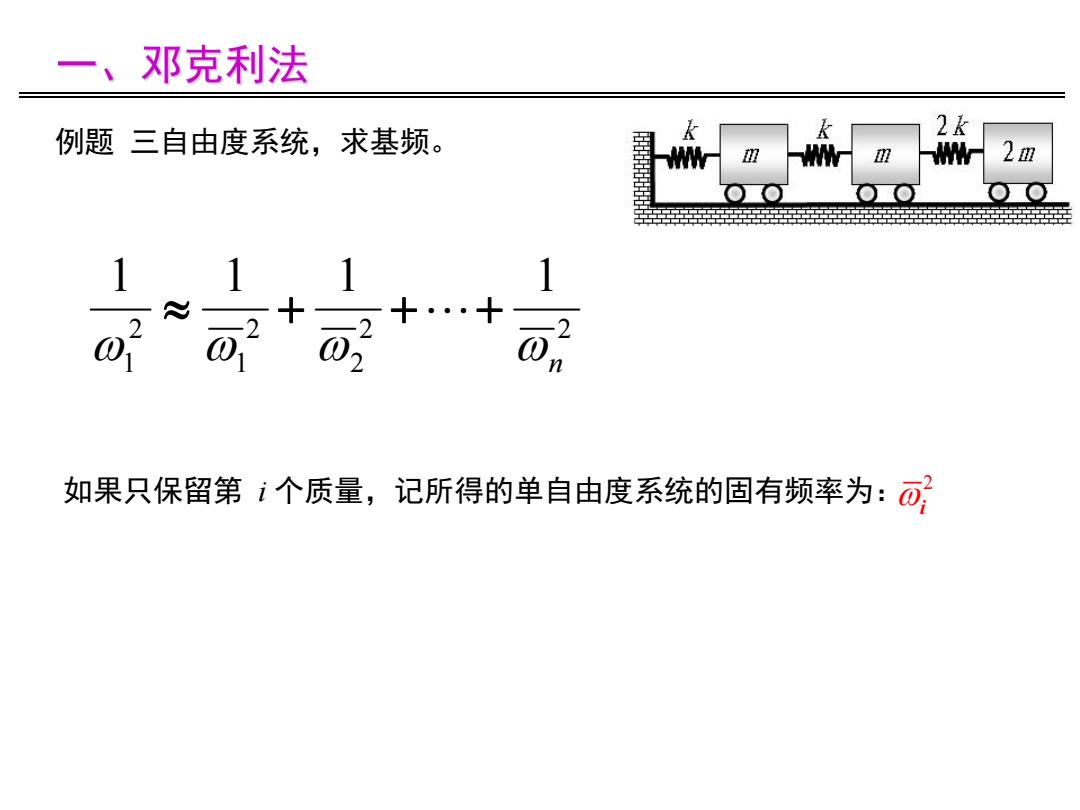
一、邓克利法 例题三自由度系统，求基频。 2& 2m 十… 01 如果只保留第i个质量，记所得的单自由度系统的固有频率为：可

例题 三自由度系统，求基频。 2 2 2 2 1 2 1 1 1 1 1    n    如果只保留第 i 个质量，记所得的单自由度系统的固有频率为： 2 i

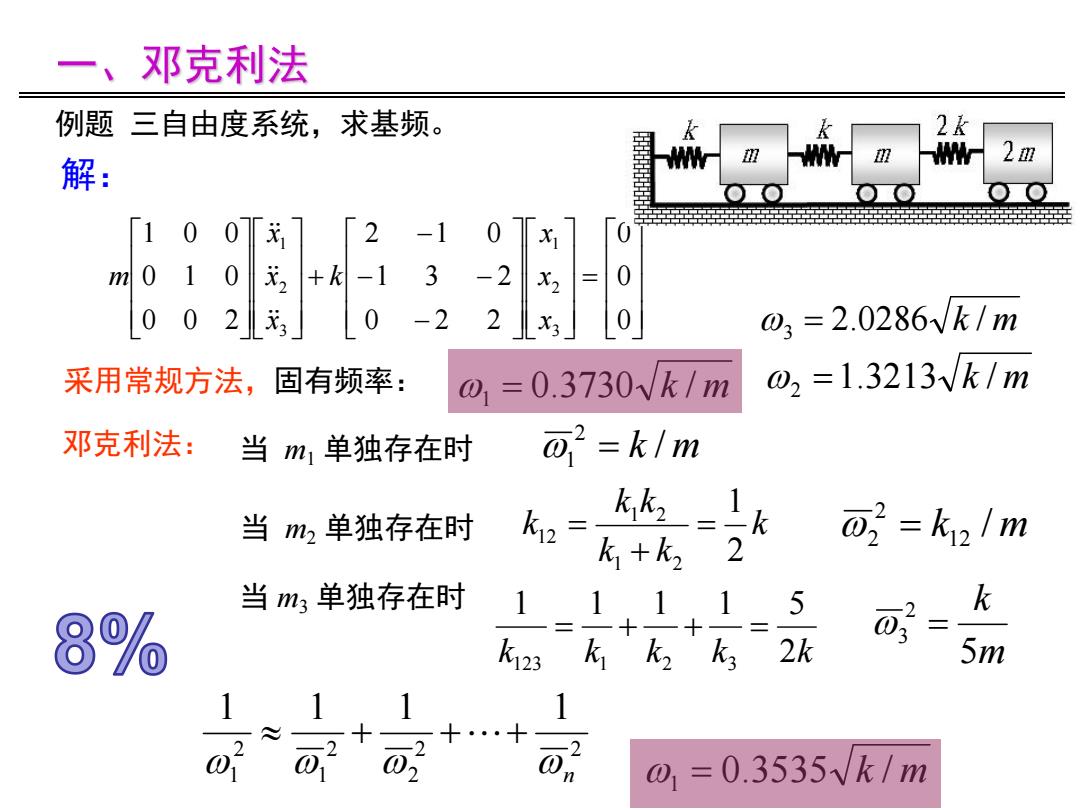
一、邓克利法 例题三自由度系统，求基频。 2k 2m 解： 10 0[ 2 -10 m 0 1 0 2 +k -1 3 -2 X2 0 0 02 x3 0 -2 2 0 03=2.0286Vk/m 采用常规方法，固有频率： =0.3730√k/m o2=1.3213Vk/m 邓克利法：当m1单独存在时 02=k/m 当m2单独存在时 k2= kikz=k k+k22 而=k2/m 当m3单独存在时 11, 1.15 k 闪 2k 5m o1=0.3535Vk/m

                                    0 0 0 0 2 2 1 3 2 2 1 0 0 0 2 0 1 0 1 0 0 3 2 1 3 2 1 x x x k x x x m    采用常规方法，固有频率： 1  0.3730 k / m 2 1.3213 k / m 3  2.0286 k / m 邓克利法： 当 m1 单独存在时 k / m 2 1  k12 / m 2 当 m2 单独存在时 k 2  k k k k k 2 1 1 2 1 2 12    当 m3 单独存在时 k k k k 2k 1 1 1 1 5 123 1 2 3     m k 5 2 3  2 2 2 2 1 2 1 1 1 1 1    n    1  0.3535 k / m 例题 三自由度系统，求基频。 解：