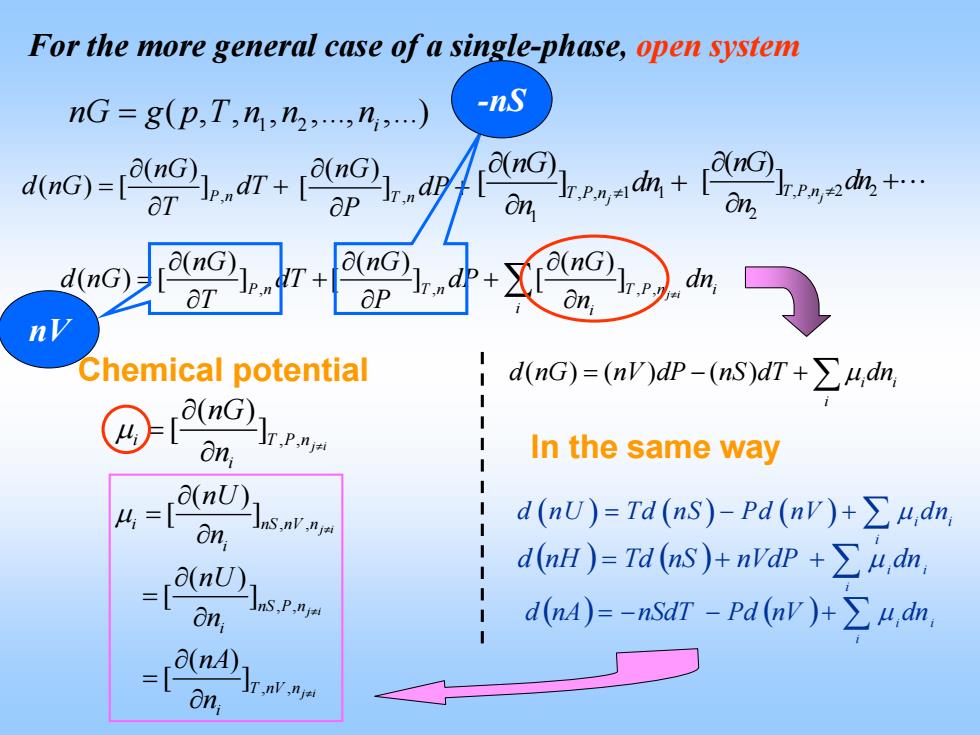
For the more general case of a single-phase,open system nG=g(p,T,h,n2,n,) -nS (nG) on, n Chemical potential dnG)=(n)dp-(nS)dT+∑4,dn (nG)1 On In the same way 4=en0) nS.nv.nja d(nU)=Td(nS)-Pd(nv)+>u,dn, -[n) d(aH)=Td(s)+ndP+∑从,dn, On; nS,P.nja d(nA)=-nSdT-Pd (nv)+udn, a(nA) on
For the more general case of a single-phase, open system 1 2 ( , , , ,., ,.) i nG g p T n n n = , , , () () () ( )[ ] [ ] [ ] P j i n T n T P n i i i nG nG nG d nG dT dP dn TP n ≠ ∂∂ ∂ = ++ ∂∂ ∂ ∑ , ( ) [ ]T n nG dP P ∂ + ∂ , 1 1 1 ( ) [ ]T Pnj nG dn n ≠ ∂ + ∂ , 2 2 2 ( ) [ ]TPnj nG dn n ≠ ∂ + ∂ d nG( )[ ] ( ) nG P n, dT L T ∂ = + ∂ , , ( ) [ ] j i i T P n i nG n μ ≠ ∂ = ∂ Chemical potential ( )( ) ( ) i i i d nG nV dP nS dT dn = −+ ∑ μ nV -nS ( ) ( ) ++= ∑i nVdPnSTdnHd μ dnii ( ) ( )+−−= ∑i nAd nVPdnSdT μ dnii ( ) ( ) ( ) i i i d nU Td nS Pd nV dn =− + ∑ μ In the same way , , , , , , ( ) [ ] ( ) [ ] ( ) [ ] j i j i j i i n S n V n i nS P n i T nV n i nU n nU n nA n μ ≠ ≠ ≠ ∂ = ∂ ∂ = ∂ ∂ = ∂

dnG)=(nWdp-(nS)dT+∑4,dn For the case of one mole of solution n-1 nxi dG=dP-SdT+∑4,a G=G(P,T,x1,x2,x,.) T )pn=-S
( )( ) ( ) i i i d nG nV dP nS dT dn = −+∑μ For the case of one mole of solution n=1 ni=xi i i i dG VdP SdT dx =−+∑μ 1 2 ( , , , ,., ,.) G GPT x x x = i , , () () T n P n G G V S P T ∂ ∂ = =− ∂ ∂
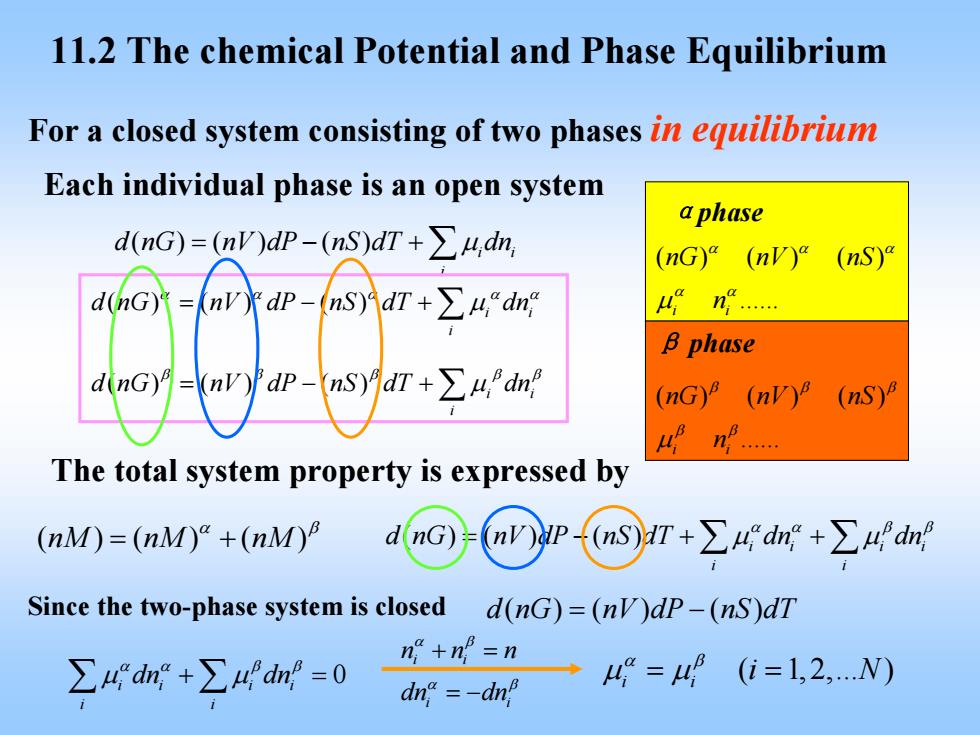
11.2 The chemical Potential and Phase Equilibrium For a closed system consisting of two phases in equilibrium Each individual phase is an open system aphase dnG)=nVdP-(nS)dT+∑4,dn (nG)"(nV) (nS) d(nG) (n水dP-ns)idr+∑4dn B phase dinG)=(nv) dP-ns)月dr+∑h,dn (nG)(nV)8 (nS) The total system property is expressed by (nM)=(nM)+(nM) Since the two-phase system is closed d(nG)=(nV)dp-(nS)dT ∑4dr+∑Adn=0 n+no=n →42=4(i=1,2,.N) dna=-dn
11.2 The chemical Potential and Phase Equilibrium For a closed system consisting of two phases in equilibrium Each individual phase is an open system αphase β phase ( ) ( ) () . i i nG nV nS n α αα α α μ ( ) ( ) () . i i nG nV nS n β ββ β β μ ( )( ) ( ) i i i d nG nV dP nS dT dn = −+ ∑ μ ( ) ( ) () i i i d nG nV dP nS dT dn α αα α α = −+ ∑ μ ( ) ( ) () i i i d nG nV dP nS dT dn β ββ β β = −+ ∑ μ The total system property is expressed by ( )( ) ( ) nM nM nM α β = + ( )( ) ( ) ii ii i i d nG nV dP nS dT dn dn α α ββ = −+ + ∑μ μ ∑ Since the two-phase system is closed d nG nV dP nS dT ( )( ) ( ) = − 0 ii ii i i dn dn αα ββ ∑ ∑ μ μ + = i i i i nnn dn dn α β α β + = = − ( 1, 2,. ) i i i N α β μ μ = =

For n-phase system 4=4==4(i=1,2,N) Multiple phases at the same T and P are in equilibrium when the chemical potential of each species is the same in all phases
For π-phase system . ( 1, 2,. ) ii i i N αβ π μμ μ = == = Multiple phases at the same T and P are in equilibrium when the chemical potential of each species is the same in all phases

11.3 Partial Properties 11.3.1 Definition of the partial molar property of species i in solution 在恒温、恒压下,物系的容量 M, a(nM 8n, 性质随某种组分摩尔数的变化率叫 TP.n 做该组分的偏摩尔性质 Solution properties M:H、S、A、U、G、,.; Pure-species properties M:H、Si、A、U、G、V,. Partial properties M:H S,A U G,V. a(nG) 4= on, -G Gibbs.之所以专门定义偏摩 尔自由焓为化学位,是由于 偏摩尔自由焓在化学平衡和 相平衡中应用较多
11.3 Partial Properties ( ) n,P,T j i i n nM M ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ = 11.3.1 Definition of the partial molar property of species i in solution 在恒温、恒压下,物系的容量 性质随某种组分摩尔数的变化率叫 做该组分的偏摩尔性质 ( ) i i n,P,T i G n nG j = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ μ = Gibbs之所以专门定义偏摩 尔自由焓为化学位,是由于 偏摩尔自由焓在化学平衡和 相平衡中应用较多。 Solution properties M : H 、 S 、 A 、 U 、 G 、V, . ; Pure-species properties Mi : Hi 、 Si 、 Ai 、 Ui 、 Gi 、 Vi, . Partial properties : , , , , , , . MH S AU GV ii i i ii