
溶液的体积、焓等性质不仅和T,有关,且与溶液的组 成有关。 对于真实溶液,溶液性质一般不等于构成它的各纯组 分性质的加和。 为找出各种物质在溶液中所“具有”的性质之间的关 系,引入“偏摩尔性质”的概念。 偏摩尔性质是溶液热力学中很重要的一类物理量 惟真帷竇
溶液的体积、焓等性质不仅和T, p有关,且与溶液的组 成有关。 对于真实溶液,溶液性质一般不等于构成它的各纯组 分性质的加和。 为找出各种物质在溶液中所“具有”的性质之间的关 系,引入“偏摩尔性质”的概念。 偏摩尔性质是溶液热力学中很重要的一类物理量
4.2.1偏摩尔性质的定义 对均相多元体系(如N元),任一热力学广度性质为 M,=nM=M(T,p,n,n.,n) 对体系的任何状态变化,有 a(nM) dn T.p.n) 外部因素 内部因素 %是指除i组分外其余所有组分的物质的量均保持不变。表 示体系中所有组分的物质的量都保持不变。 惟真帷竇
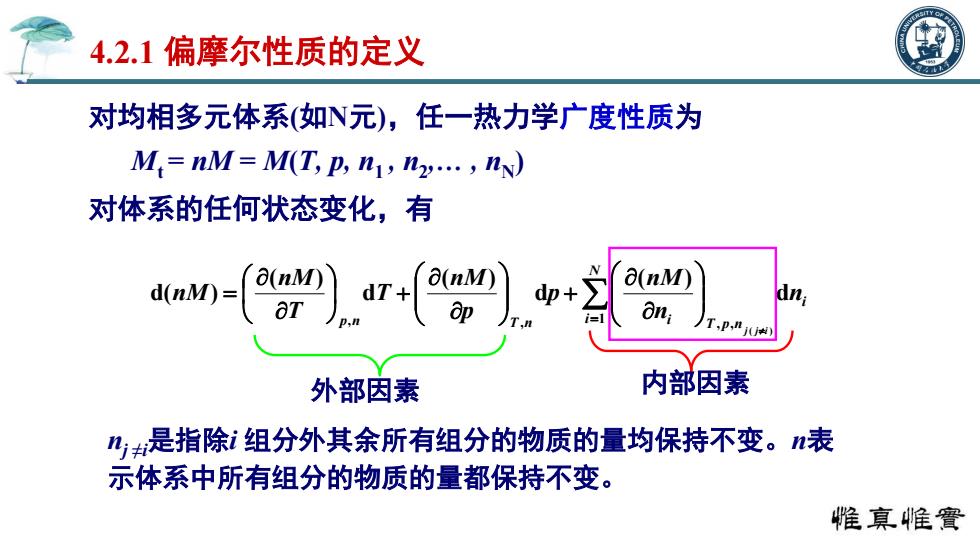
对均相多元体系(如N元),任一热力学广度性质为 Mt = nM = M(T, p, n1 , n2 ,. , nN ) 对体系的任何状态变化,有 4.2.1 偏摩尔性质的定义 i T p n N p n T n i i n n nM p p nM T T nM nM j j i d ( ) d ( ) d ( ) d( ) ( ) , , 1 , , 外部因素 内部因素 nj ≠i是指除i 组分外其余所有组分的物质的量均保持不变。n表 示体系中所有组分的物质的量都保持不变
4.2.1偏摩尔性质的定义 定义:溶液中组分i的偏摩尔性质M; M OM (nM) On On (4-18) T,p,njti T,p,njti M,称为在指定T,p和组成下组分i的偏摩尔性质。 M泛指溶液的摩尔热力学性质,如U,H,S,A,G,C,等。 最有用的是7五,G 惟真帷竇
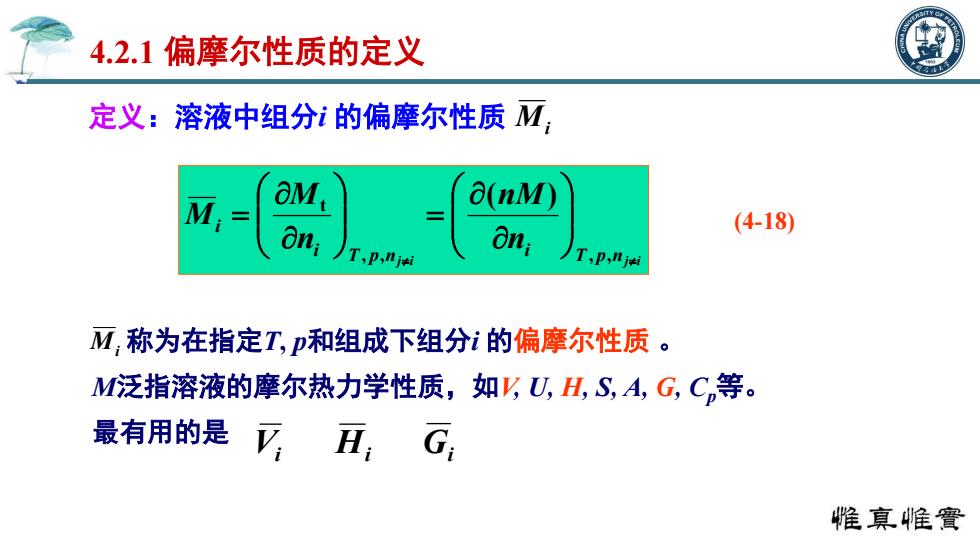
定义:溶液中组分i 的偏摩尔性质 4.2.1 偏摩尔性质的定义 称为在指定T, p和组成下组分i 的偏摩尔性质 。 M泛指溶液的摩尔热力学性质,如V, U, H, S, A, G, Cp等。 最有用的是 Mi j i nj i T p n i T p i i n nM n M M , , , , t ( ) (4-18) Mi Vi Hi Gi

4.2.1偏摩尔性质的定义 偏摩尔性质的物理意义 ◆恒温恒压下,在无限大量的体系中,除了组分外保持其它组分的 量不变,加入1oli组分时所引起的体系某一广度性质总量的变化, 即为偏摩尔性质。 ◆恒温恒压下,在有限量的体系中,除了组分外保持其它组分的量 不变,加入dn;mol i组分时所引起的体系某一广度性质的变化与dn 的比值,即为偏摩尔性质。 ◆这两种说法都是要维持体系不引起总浓度的变化。 惟真帷竇
偏摩尔性质的物理意义 恒温恒压下,在无限大量的体系中,除了i组分外保持其它组分的 量不变,加入1mol i 组分时所引起的体系某一广度性质总量的变化, 即为偏摩尔性质。 恒温恒压下,在有限量的体系中,除了i组分外保持其它组分的量 不变,加入dnimol i 组分时所引起的体系某一广度性质的变化与dni 的比值,即为偏摩尔性质。 这两种说法都是要维持体系不引起总浓度的变化。 4.2.1 偏摩尔性质的定义
4.2.1偏摩尔性质的定义 以体积为例说明如下: 加入1mol 加入dn,mol的 i组分 i组分 极大量,T,p常数 有限量,工,p常数 除i外, 除i外, 其他组分不变 其他组分不变 体系的体积从nV变化到nV+△V, 体系的体积从n变化到n+d(n), 那么 那么 7,=AV T.p,nit 惟真帷竇
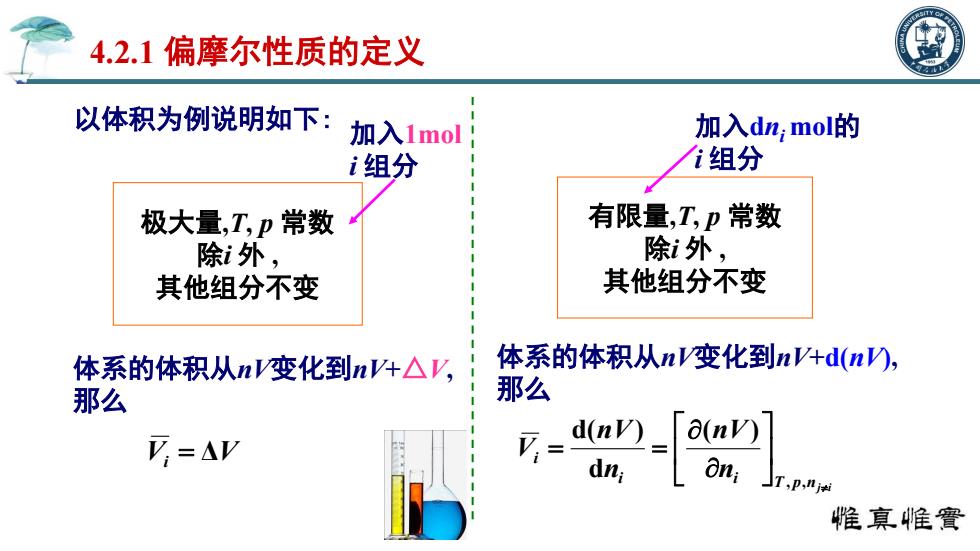
以体积为例说明如下: Vi ΔV 4.2.1 偏摩尔性质的定义 极大量,T, p 常数 除i 外 , 其他组分不变 加入1mol i 组分 体系的体积从nV变化到nV+△V, 那么 有限量,T, p 常数 除i 外 , 其他组分不变 加入dni mol的 i 组分 体系的体积从nV变化到nV+d(nV), 那么 T p nj i i i i n nV n nV V , , ( ) d d( )