
对dp=pdW进行积分可得 p=pW+C 如果已知平衡液体边界上(或液体内)某点的压强为P。、 力势函数为W。 则积分常数 C=Po-pWo 得 p=P。+pW-W) 结论:平衡液体中,边界上的压强将等值地传递到液体内的 一切点上;即当P。增大或减小时,液体内任意点的压强也 相应地增大或减小同样数值。 这就是物理学中著名的巴斯加原理。 金4>EXT

第二章水静力学 三、等压面的概念 静止液体中由压强相等的点连成的面,称为等压 面。等压面可以是平面,也可以是曲面。 可以证明: ■等压面必与质量力正交,这是等压面的一个重要特性。 只受重力作用的连通的同一种液体内,等压面为水平面。 In"in Mns 连通容器 连通器被隔断

证明:设想某一质点液体M在等压面上移动一微分距离ds,设 质点的单位质量力及ds矢量为: f=Xi+万+Zk ds dxi+dyj+dzk 则作用在质点上的质量力做功应为: dm·f·ds.cos0=f.ds,dm=dm(Xdk+Yy+Zd) 0一于和d的夹角 即质量力做功=它在各轴向分力做功之和。 又,在平衡液体等压面上p=Const 因此dp=p(Xk+Y+Zb)=0 f·d5=0即fds cos0=0 :f≠05≠0 ∴c0s0=0→0=90 返回 .于⊥d本=0质量力与ds正交 →质量力与等压面正交。 ds是等压面上的任意两邻点的线矢
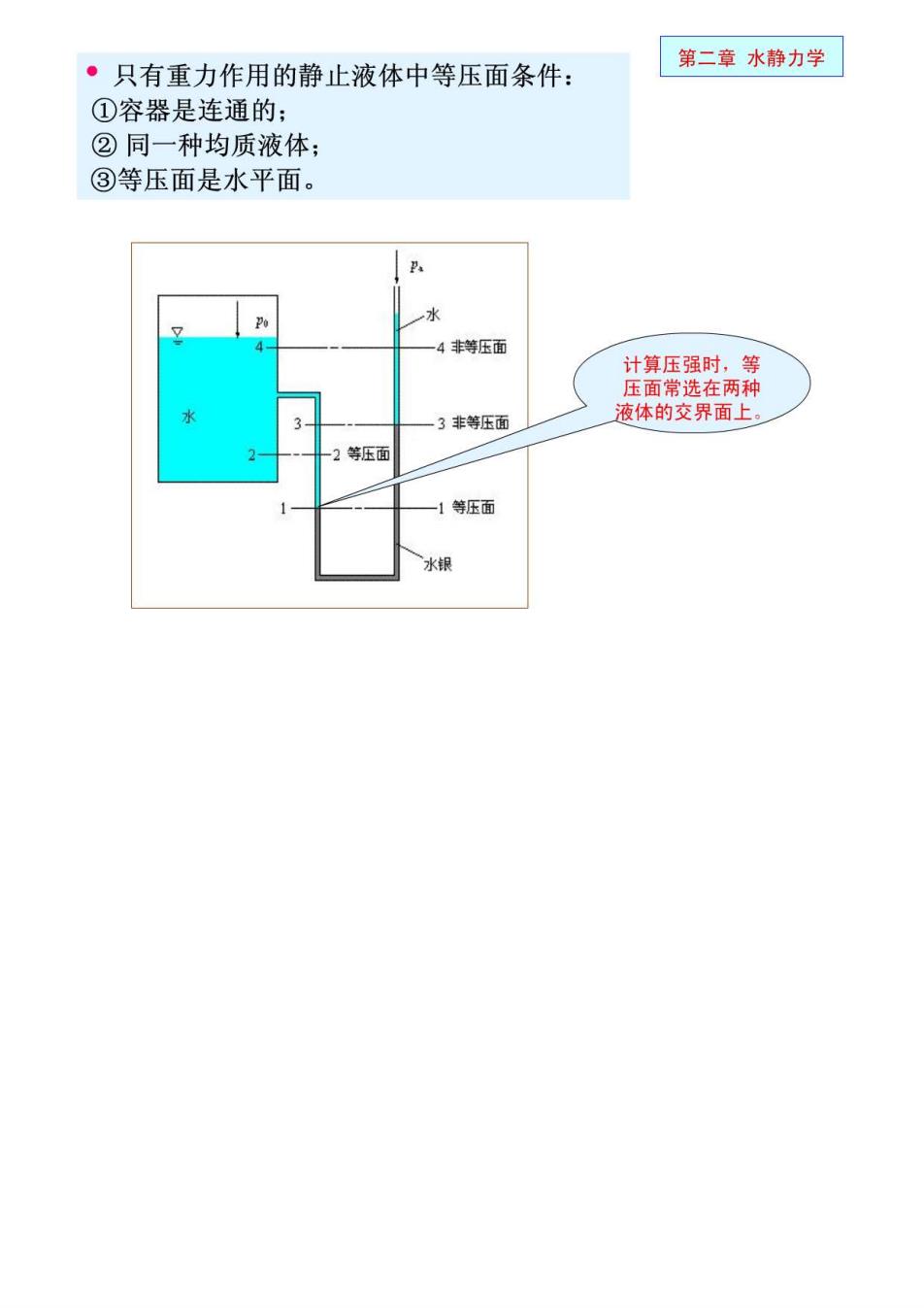
·只有重力作用的静止液体中等压面条件: 第二章水静力学 ①容器是连通的: ②同一种均质液体: ③等压面是水平面。 4非等压面 计算压强时,等 压面常选在两种 3非等压面 液体的交界面上。 2等压面 等压面 水银

2.3重力和几种质量力同时作用下液体的平衡 一、重力作用下静水压强的基本公式 ·水静力学的基本方程 重力作用下静止液体单位质量力: X=Y=0,Z=-g 代入液体平衡微分方程: dp=p(Xd +Ydy+Zdz) dp =-pgdz =-ydz 积分 p=-Yz+C 在自由液面上有:z=H,p=P。 C=Po+yH