
第二章水静力学 二、静水压强的特性: 1、静水压强的方向垂直指向受压面 静止液体表面应力只能是压应力 或压强,且静水压强方向与作用面的 内法线方向重合。 因为静止液体不能承受切力和拉力,所以平行于作 用面的切力等于零,且静水压强必然垂直指向受压 面
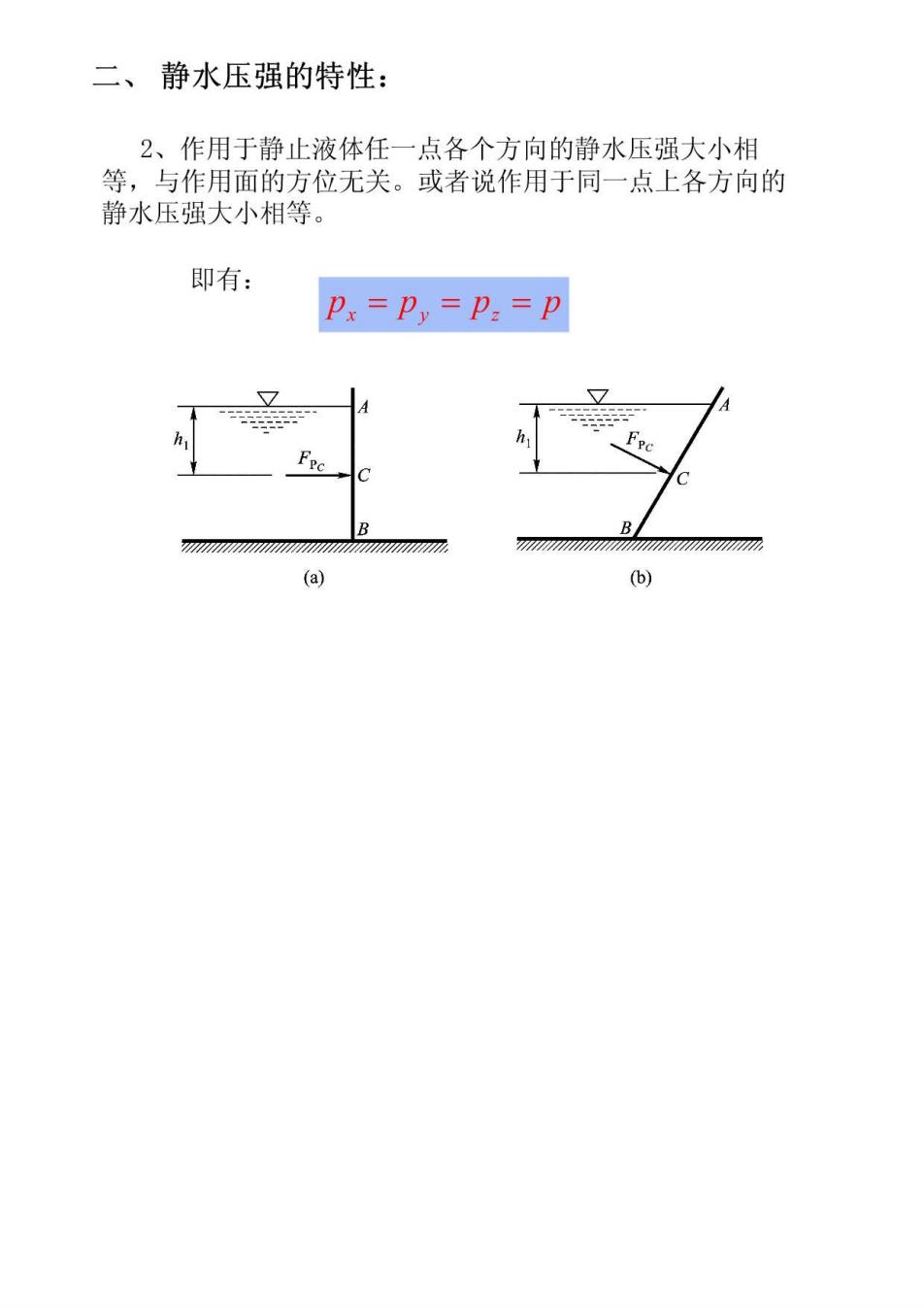
二、静水压强的特性: 2、作用于静止液体任一点各个方向的静水压强大小相 等,与作用面的方位无关。或者说作用于同一点上各方向的 静水压强大小相等。 即有: Px=Py=P:=p ☑ p 6

证明:从平衡状态下的液体中取一微元四面体OABC,如图所示取坐标轴。 由于液体处于平衡状态,则有∑F=0,即各坐标方向分力投影之和 亦为零,则: dp.dp,cos(n,x)+dF.=0 dP,-dP,cos(n,y)+dF,=0 dP.-dP,cos(n,z)+dF.=0 dpn B x方向受力分析: dp, dps 识=p2t 0 表面力: X dp, dP,cos(n,x)=p,A,cos(n,x)=pdoidk n为斜面ABC的法线方向 质量力:F=X·ovk/6 防合东p-p.s+Xp哈d=0 1 化简得: Px-Pn+dc·pX=0

x方向合力: Px-Pn+dk·pX=0 dpn B 当四面体无限地趋于o点时,则dx0,所以有:dp、 dp, P=Pn 0 C 类似地有: P=P=P.=Pn dpz 而n是任意选取的,所以同二点静压强大小 相等,与作用面的方位无关。 说明:(1)静止液体中不同点的压强一般是不相等的,同一点的各方向 静水压强大小相等。 (2)运动状态下的实际液体层间有相对运动,则由于粘性会产生切 应力,这时同一点上各法向应力不再相等
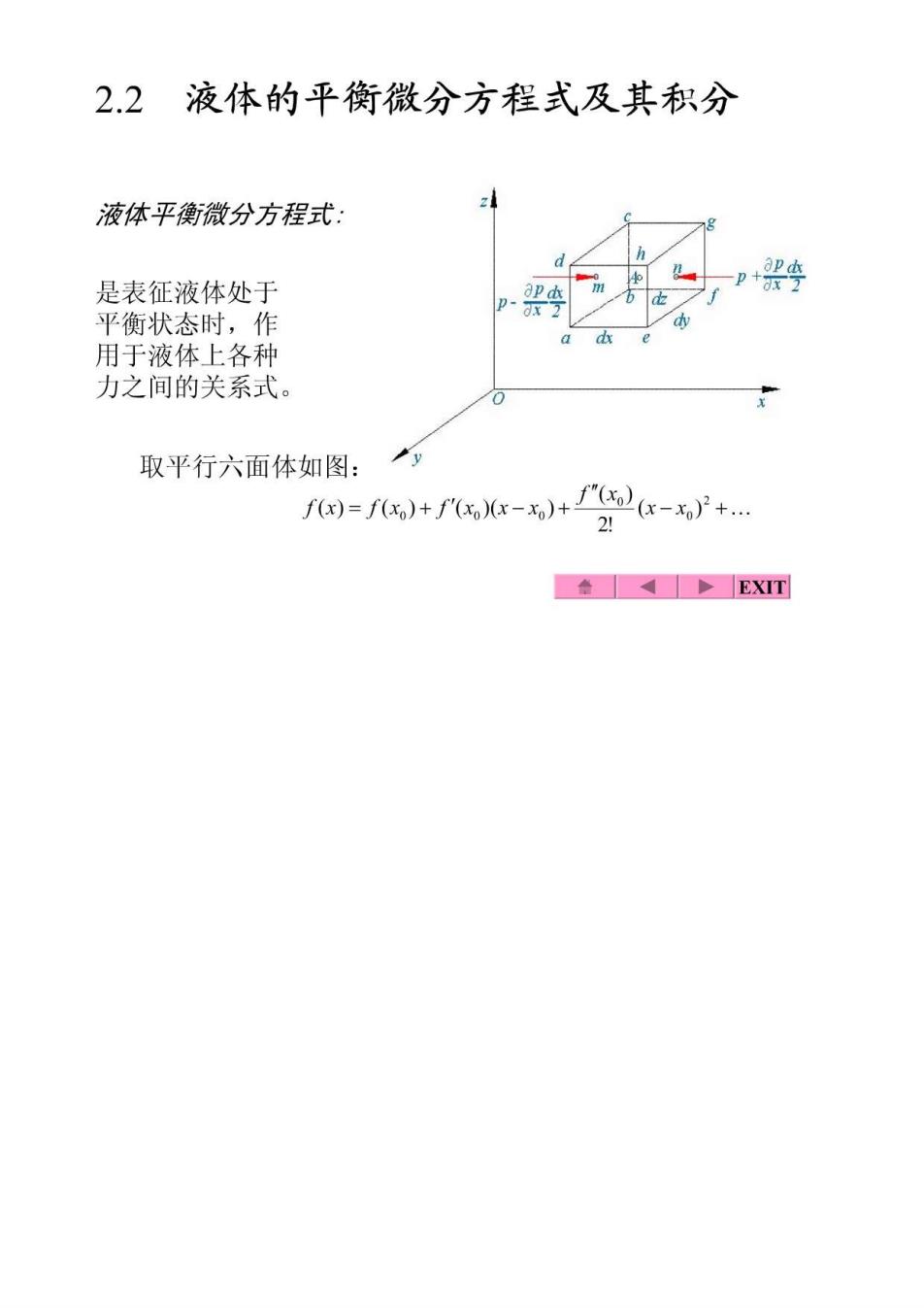
2.2液体的平衡微分方程式及其积分 液体平衡微分方程式: + 是表征液体处于 平衡状态时,作 用于液体上各种 力之间的关系式。 取平行六面体如图: f)=f)+f0xx-x)+"x-+ 21 金4>EXT